Функция квадратного корня Python

>>> n = 5
>>> x = n**2
>>> x
25


Оператор Python ** используется для вычисления степени числа. В данном случае 5 в квадрате, или 5 в степени 2, равно 25.
Квадратный корень, таким образом, равен числу n, которое при умножении само на себя дает квадрат, x.
В этом примере n, квадратный корень из 25, равен 5.
25 - это пример  идеального квадрата. Идеальные квадраты - это квадраты целых значений:

>>> 1**2
1

>>> 2**2
4

>>> 3**2
9


Возможно, вы запомнили некоторые из этих идеальных квадратов, когда учили таблицу умножения на уроке элементарной алгебры.
Если вам задан маленький идеальный квадрат, возможно, будет достаточно просто вычислить или запомнить квадратный корень из него. Но для большинства других квадратов это вычисление может оказаться немного более утомительным. Часто оценка оказывается достаточно точной и тогда, когда у вас нет калькулятора.
К счастью, у вас, как у разработчика Python, есть калькулятор, а именно интерпретатор Python!
Функция квадратного корня Python
Модуль Python math в стандартной библиотеке может помочь вам работать с математическими задачами в коде. Он содержит множество полезных функций, таких как remainder() и factorial(). Он также включает в себя функцию квадратного корня Python, sqrt().
Вы начнете с импорта math:

>>> import math


Это все, что нужно! Теперь вы можете использовать math.sqrt() для вычисления квадратных корней.
sqrt() имеет простой интерфейс. Он принимает один параметр, x, который, как вы видели ранее, обозначает квадрат, из которого вы хотите извлечь квадратный корень. В приведенном ранее примере это было бы 25.
Возвращаемое значение sqrt() является квадратным корнем из x в виде  числа с плавающей запятой. В приведенном примере это будет выглядеть следующим образом 5.0.
Далее вы ознакомитесь с некоторыми примерами того, как использовать sqrt() и как не использовать sqrt().
Квадратный корень из положительного числа
Один из типов аргументов, который вы можете передать в sqrt(), - это положительное число. Это включает в себя как типы int, так и float.
Например, вы можете найти квадратный корень из 49, используя sqrt():

>>> math.sqrt(49)
7.0


Возвращаемое значение равно 7.0, квадратному корню из 49, в виде числа с плавающей запятой.
Наряду с целыми числами вы также можете передавать float значения:

>>> math.sqrt(70.5)
8.396427811873332


Вы можете проверить точность этого квадратного корня, вычислив его обратную величину:

>>> 8.396427811873332**2
70.5


Квадратный корень из нуля
Даже 0 является допустимым квадратом для передачи функции квадратного корня Python:

>>> math.sqrt(0)
0.0


Хотя вам, вероятно, не придется часто вычислять квадратный корень из нуля, вы, возможно, передаете переменную в sqrt(), значение которой вы на самом деле не знаете. Итак, полезно знать, что в таких случаях он может работать с нулем.
Квадратный корень из отрицательных чисел
 Квадрат любого действительного числа не может быть отрицательным. Это связано с тем, что отрицательное произведение возможно только в том случае, если один множитель положительный, а другой отрицательный. Квадрат, по определению, является произведением числа на него самого, поэтому невозможно получить отрицательный действительный квадрат: 

>>> math.sqrt(-25)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: math domain error


Если вы попытаетесь передать отрицательное число в sqrt(), то получите ValueError, потому что отрицательные числа не входят в область возможных действительных квадратов. Вместо этого квадратный корень из отрицательного числа должен быть сложным, что выходит за рамки функции квадратного корня Python.
Квадратные корни в реальном мире
Чтобы увидеть реальное применение функции извлечения квадратного корня из Python, вы можете обратиться к теннису.
Представьте, что Алекс де Минаур, один из самых быстрых игроков в мире, только что нанес удар справа в дальний угол, где базовая линия пересекается с боковой линией .>теннисный корт:

Теперь предположим, что его соперник нанес ответный удар дроп—шотом, который отправил бы мяч в дальний угол с небольшим импульсом движения вперед — в противоположный угол, где другая боковая линия пересекается с сеткой:

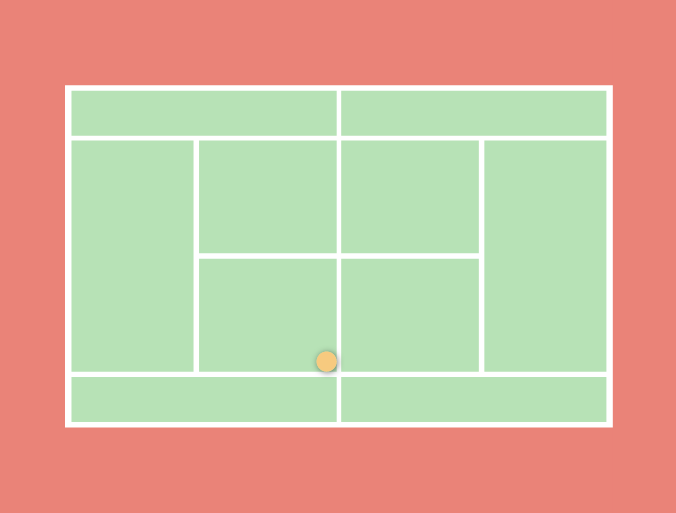
Как далеко должен пробежать Надаль, чтобы дотянуться до мяча?
Исходя из нормативных размеров теннисного корта, вы можете определить, что длина базовой линии составляет 27 футов, а боковой линии с одной стороны сетки - 39 футов. Итак, по сути, это сводится к решению задачи для гипотенузы прямоугольного треугольника:

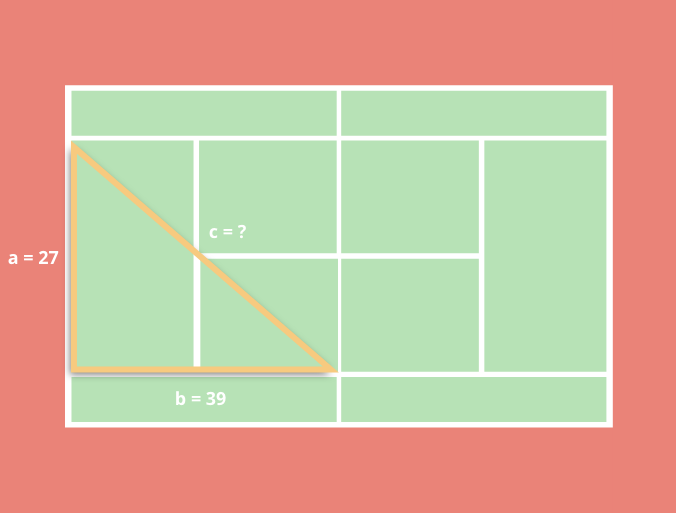
Используя ценное уравнение из геометрии, Теорему Пифагора, вы знаете, что a2 + b2 = c2, где a и b - это катеты прямоугольного треугольника, а c - гипотенуза.
Таким образом, вы можете рассчитать расстояние, которое должен пробежать Надаль, изменив порядок решения уравнения для c:

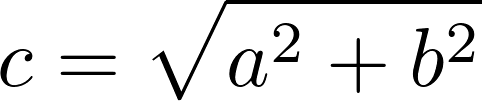
Вы можете решить это уравнение, используя функцию квадратного корня Python:

>>> a = 27
>>> b = 39
>>> math.sqrt(a**2 + b**2)
47.43416490252569


Итак, Надалю нужно пробежать около 47,4 футов (14,5 метров), чтобы дотянуться до мяча и сохранить очко.
Заключение
Поздравляем! Теперь вы знаете все о функции квадратного корня в Python.
В этом руководстве вы рассмотрели:

Краткое введение в квадратные корни
Все тонкости функции квадратного корня в Python, sqrt()
Практическое применение sqrt() на примере реального мира

Умение использовать sqrt() - это только часть уравнения. Понимание того, когда его использовать, не менее важно. Теперь, когда вы знаете и то, и другое, продолжайте применять свое новообретенное мастерство в использовании функции квадратного корня Python!
Часто задаваемые вопросы
Теперь у вас есть некоторый опыт работы с квадратными корнями в Python. Ниже вы найдете несколько вопросов и ответов, которые обобщают наиболее важные концепции, рассмотренные в этом руководстве.
Вы можете использовать эти вопросы, чтобы проверить свое понимание или обобщить и закрепить то, что вы только что узнали. После каждого вопроса вы найдете краткое объяснение, спрятанное в разборном разделе. Нажмите на переключатель Показать/скрыть, чтобы открыть ответ.


Чтобы найти квадратный корень в Python, вы используете функцию math.sqrt(). Сначала импортируйте модуль math, затем вызовите math.sqrt() с числом, из которого вы хотите найти квадратный корень. Например, math.sqrt(16) возвращает 4.0.


Да, вы можете вычислить квадратный корень из отрицательных чисел в Python, но не с помощью функции math.sqrt(). Вместо этого вам следует использовать cmath.sqrt(). Попытка вычислить квадратный корень из отрицательного числа с помощью math.sqrt() приведет к результату ValueError, поскольку эта функция не может обрабатывать отрицательные числа.


Вы можете использовать как math.sqrt(), так и pow() для нахождения квадратного корня в Python. Хотя оба варианта возвращают один и тот же результат для неотрицательных чисел, math.sqrt() более удобочитаем и специально разработан для этой цели.


Чтобы использовать функцию квадратного корня в Python, вам необходимо импортировать ее из модуля math. Используйте оператор import math, а затем вызовите math.sqrt(), чтобы найти квадратный корень из числа.


Да, вы можете вычислить квадратный корень, не импортируя модуль math, используя оператор возведения в степень ** или встроенную функцию pow(). Например, 4**0.5 вернет 2.0, что даст вам тот же результат, что и math.sqrt().
<статус завершения article-slug="python-функция с квадратным корнем" class="btn-group mb-0" data-api-article-bookmark-url="/api/v1/articles/python-функция с квадратным корнем/bookmark/" data-api-статья-статус завершения-url="/api/v1/articles/python-функция с квадратным корнем/завершение_статуса/">



<кнопка поделиться bluesky-text="Интересная статья на #Python от @realpython.com :" email-body="Ознакомьтесь с этой статьей о Python:%0A%0 Функция квадратного корня в Python" email-subject="Статья о Python для вас" twitter-text="Интересная статья о Python от @realpython:" url="https://realpython.com/python-square-root-function /" url-title="Функция квадратного корня Python">

 Смотрите сейчас, к этому уроку прилагается соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным руководством, чтобы углубить свое понимание:  Функция извлечения квадратного корня в Python

                







                 Back to Top