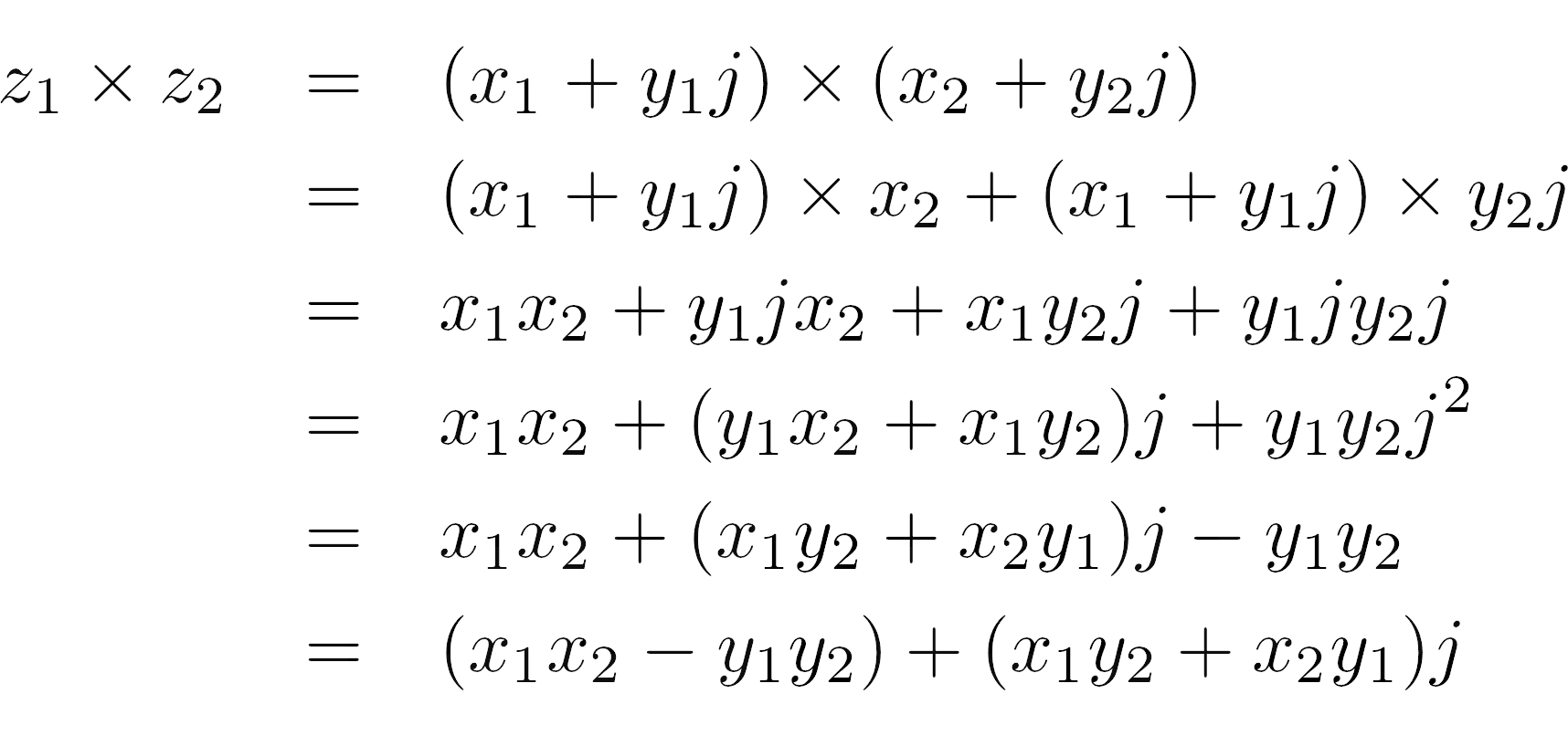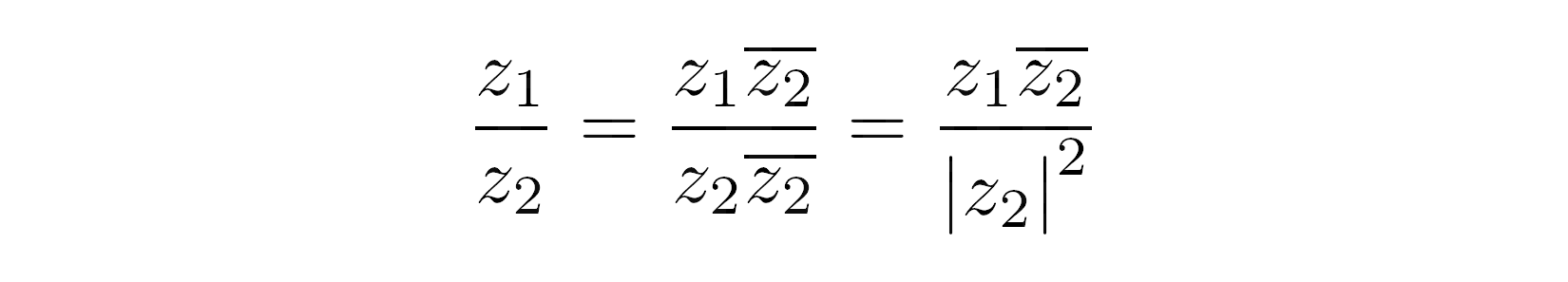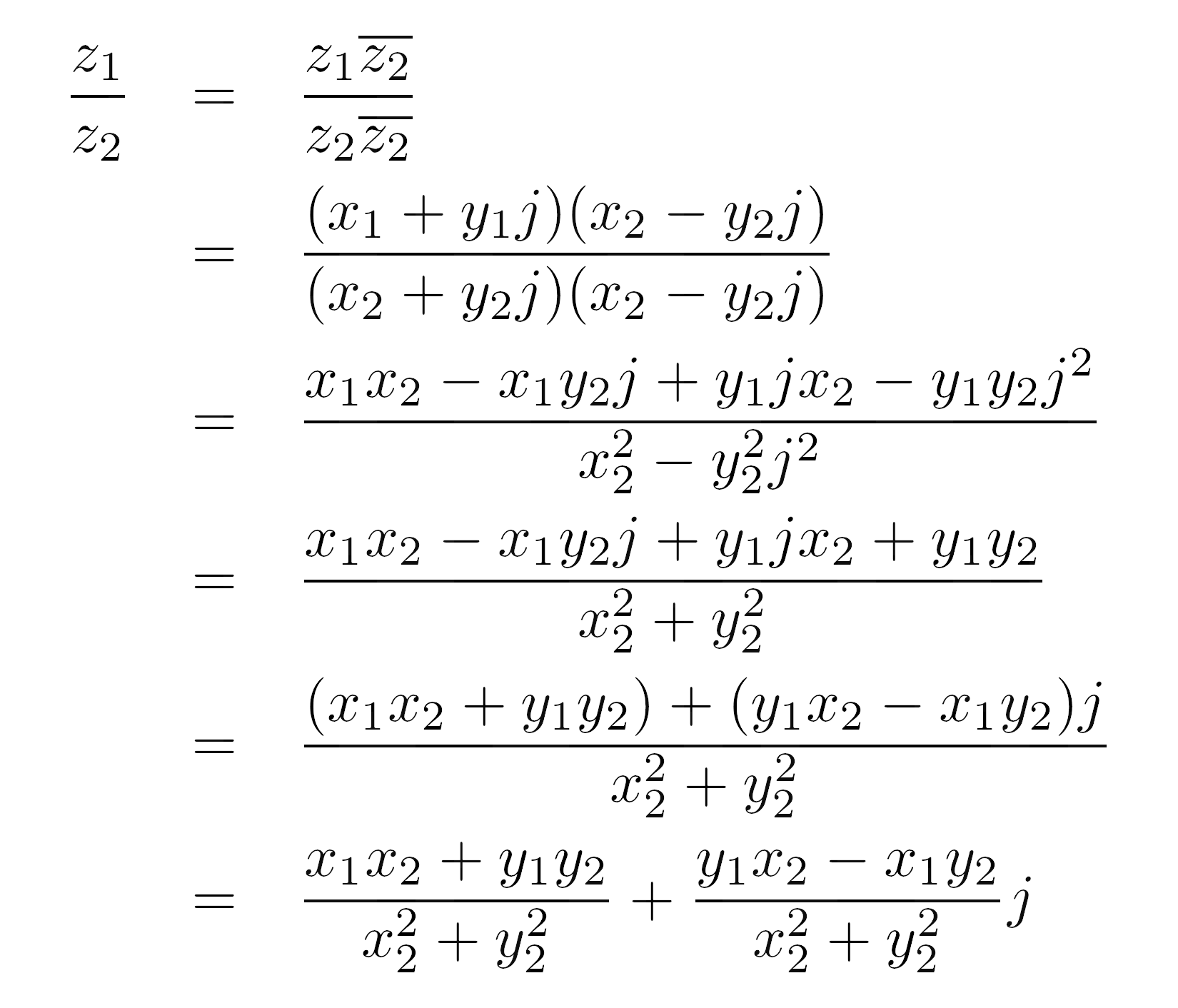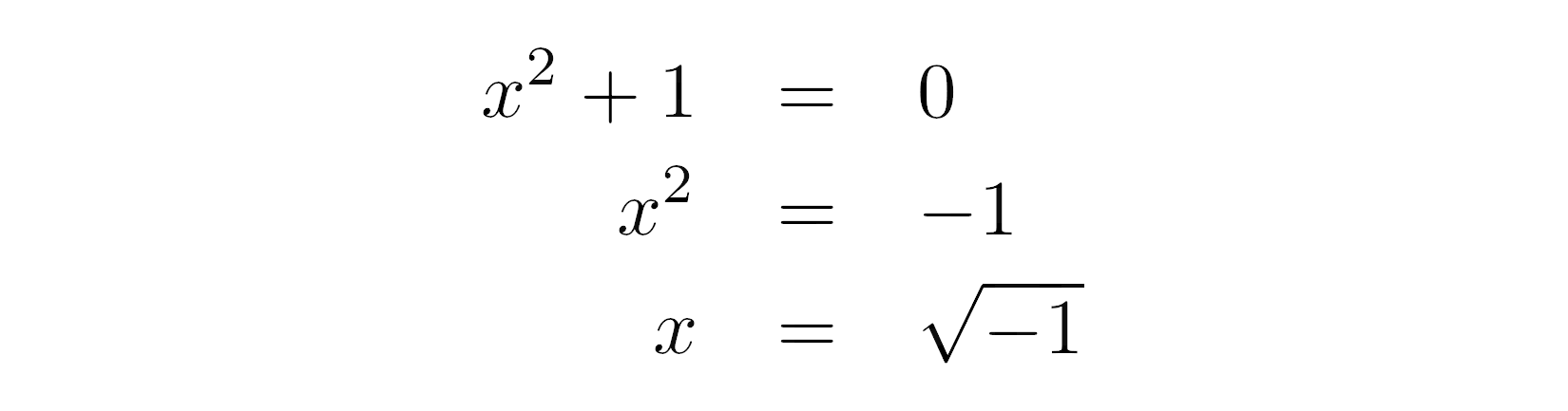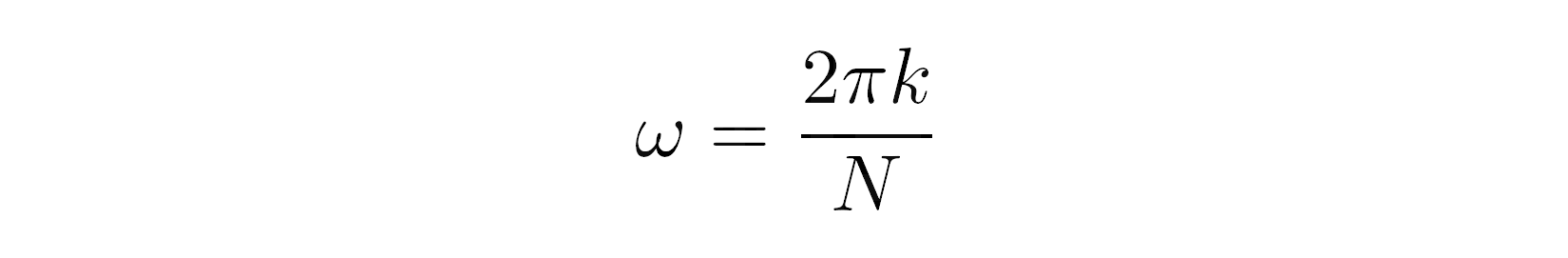Упрощение сложных чисел с помощью Python

Оглавление

• Создание комплексных чисел в Python
  • Литерал комплексного числа
  • сложная() Заводская функция
• Знакомство с комплексными числами Python
  • Доступ к реальным и мнимым частям
  • Вычисление сопряженного комплексного числа
• Арифметика комплексных чисел
  • Сложение
  • Вычитание
  • Умножение
  • Деление
  • Возведение в степень
• Использование комплексных чисел Python в качестве двумерных векторов
  • Получение координат
  • Вычисление величины
  • Нахождение расстояния между двумя Точками
  • Перемещение, переворачивание, масштабирование и вращение
• Изучение математического модуля для комплексных чисел: cmath
  • Извлечение корня из комплексного числа
  • Преобразование между прямоугольными и полярными координатами
  • Представление комплексных чисел по-разному
• Разбор комплексного числа в Python
  • Проверка равенства комплексных чисел
  • Упорядочение комплексных чисел
  • Форматирование комплексных чисел в виде строк
  • Создание Вашего собственного сложного типа данных
• Вычисление дискретного преобразования Фурье с комплексными числами
• Заключение

Большинство языков программирования общего назначения либо не поддерживают, либо имеют ограниченную поддержку комплексных чисел. Обычно вы можете воспользоваться каким-нибудь специализированным инструментом, таким как MATLAB, или найти стороннюю библиотеку. Python является редким исключением, поскольку в него встроены комплексные числа.

Несмотря на название, комплексные числа не являются сложными! Они удобны для решения практических задач, с которыми вы познакомитесь в этом руководстве. Вы изучите векторную графику и анализ звуковых частот, но комплексные числа также могут помочь в рисовании фракталов, например, множество Мандельброта .

В этом руководстве вы узнаете, как:

• Определение комплексных чисел с помощью литералов в Python
• Представляют комплексные числа в прямоугольных и полярных координатах
• Используйте комплексные числа в арифметических выражениях
• воспользуйтесь встроенным cmath модуль
• Переводить математические формулы непосредственно в код Python

Если вам нужно быстро освежить в памяти или ввести в курс теории комплексных чисел, то вы можете посмотреть серию видеороликов Академии Хана . Чтобы загрузить пример кода, который используется в этом руководстве, перейдите по ссылке ниже:

Получите пример кода: Нажмите здесь, чтобы получить пример кода, который вы будете использовать для изучения комплексных чисел в Python в этом руководстве.

Создание комплексных чисел в Python

Создание комплексных чисел и манипулирование ими в Python не сильно отличается от других встроенных типов данных, в частности числовых типов. Это возможно, потому что язык рассматривает их как первоклассных пользователей. Это означает, что вы можете выражать математические формулы, содержащие комплексные числа, с небольшими накладными расходами.

Python позволяет использовать комплексные числа в арифметических выражениях и вызывать функции для них точно так же, как вы бы использовали другие числа в Python. Это приводит к элегантному синтаксису, который читается почти как учебник по математике.

Литерал комплексного числа

Самый быстрый способ определить комплексное число в Python - это ввести его литерал непосредственно в исходный код:

>>> z = 3 + 2j

Хотя это и выглядит как алгебраическая формула, выражение справа от знака равенства уже является фиксированным значением, которое не нуждается в дальнейшем вычислении. Когда вы проверите его тип, вы убедитесь, что это действительно комплексное число:

>>> type(z)
<class 'complex'>

Чем это отличается от сложения двух чисел с помощью оператора "плюс" ? Очевидным признаком является буква j, приклеенная ко второму числу, что полностью меняет смысл выражения. Если бы вы убрали букву, то вместо нее получили бы знакомый целочисленный результат:

>>> z = 3 + 2

>>> type(z)
<class 'int'>

Кстати, числа с плавающей запятой можно использовать и для создания комплексных чисел:

>>> z = 3.14 + 2.71j
>>> type(z)
<class 'complex'>

Литералы комплексных чисел в Python имитируют математическую нотацию, которая также известна как стандартная форма , алгебраическая форма, или иногда каноническая форма комплексного числа. В Python вы можете использовать либо строчные j, либо прописные J в этих литералах.

Если вы изучали комплексные числа на уроках математики, то, возможно, видели, что они выражаются с помощью i вместо j. Если вам интересно, почему Python использует j вместо i, то вы можете развернуть раздел "Сворачиваемый" ниже, чтобы узнать больше.

 

В традиционном обозначении комплексных чисел используется буква i вместо j, поскольку она обозначает мнимую единицу. Если у вас есть математическое образование, вы можете почувствовать некоторый дискомфорт в связи с соглашением Python. Однако есть несколько причин, которые могут оправдать спорный выбор Python:

• Это соглашение, уже принятое инженерами, чтобы избежать коллизий названий с электрическим током, который обозначается буквой i.
• В вычислительной технике буква i часто используется для обозначения переменной индексации в циклах.
• Букву i можно легко спутать с l или 1 в исходном коде.

Эта проблема была обнаружена в системе отслеживания ошибок Python более десяти лет назад, и сам создатель Python, Гвидо ван Россум, закрыл проблему следующим комментарием:

Это не будет исправлено. Во-первых, буква "i" или заглавная буква "I" слишком похожи на цифры. Способ анализа чисел либо с помощью языкового анализатора (в исходном коде), либо с помощью встроенных функций (int, float, complex) не должен быть локализуемым или настраиваемым каким-либо образом; это может привести к огромным разочарованиям в будущем. Если вы хотите анализировать комплексные числа, используя "i" вместо "j", у вас уже есть множество доступных решений. (Источник)

Вот и все. Если вы не хотите начать использовать MATLAB, вам придется смириться с использованием j для обозначения ваших комплексных чисел.

Алгебраическая форма комплексного числа соответствует стандартным правилам алгебры, что удобно при выполнении арифметических действий. Например, сложение обладает коммутативным свойством, которое позволяет менять местами порядок следования двух частей литерала комплексного числа без изменения его значения:

>>> 3 + 2j == 2j + 3
True

Аналогично, вы можете заменить сложение на вычитание в литерале комплексного числа, потому что знак минус - это просто сокращенное обозначение эквивалентной формы:

>>> 3 - 2j == 3 + (-2j)
True

Всегда ли комплексный числовой литерал в Python должен состоять из двух чисел? Может ли их быть больше? Упорядочены ли они? Чтобы ответить на эти вопросы, давайте проведем несколько экспериментов. Неудивительно, что если вы укажете только одно число, без буквы j, то в итоге получите обычное целое число или число с плавающей запятой:

>>> z = 3.14
>>> type(z)
<class 'float'>

С другой стороны, добавление буквы j к числовому литералу немедленно преобразует его в комплексное число:

>>> z = 3.14j
>>> type(z)
<class 'complex'>

Строго говоря, с математической точки зрения, вы только что создали чистое мнимое число, но Python не может представить его как отдельный тип данных. Следовательно, без другой части это просто комплексное число.

Как насчет обратного? Чтобы создать комплексное число без мнимой части, вы можете воспользоваться нулем и сложить или вычесть его следующим образом:

>>> z = 3.14 + 0j
>>> type(z)
<class 'complex'>

На самом деле, обе части комплексного числа всегда присутствуют. Если вы не видите единицу, это означает, что она имеет нулевое значение. Давайте проверим, что произойдет, если вы попытаетесь ввести в сумму больше слагаемых, чем раньше:

>>> 2 + 3j + 4 + 5j
(6+8j)

На этот раз ваше выражение больше не является литералом, потому что Python преобразовал его в комплексное число, состоящее всего из двух частей. Помните, что основные правила алгебры распространяются и на комплексные числа, поэтому, если вы сгруппируете похожие термины и примените сложение по компонентам, то в итоге получите 6 + 8j.

Обратите внимание, что по умолчанию в Python отображаются комплексные числа. Их текстовое представление содержит пару круглых скобок, строчную букву j и никаких пробелов. Кроме того, мнимая часть стоит на втором месте.

Комплексные числа, которые также являются чисто мнимыми числами, отображаются без круглых скобок и раскрывают только свою мнимую часть:

>>> 3 + 0j
(3+0j)
>>> 0 + 3j
3j

Это помогает отличить мнимые числа от большинства комплексных чисел, состоящих из действительной и мнимой частей.

complex() Заводская функция

В Python есть встроенная функция complex(), которую вы можете использовать в качестве альтернативы литералу комплексного числа:

>>> z = complex(3, 2)

В таком виде это напоминает кортеж или упорядоченную пару обычных чисел. Аналогия не такая уж притянутая за уши. Комплексные числа имеют геометрическую интерпретацию в декартовой системе координат, которую вы вскоре изучите. Комплексные числа можно рассматривать как двумерные.

Интересный факт: В математике комплексные числа традиционно обозначаются буквой z, поскольку это следующая буква в алфавите после x и y, которые обычно обозначают координаты.

Комплексное число Заводская функция принимает два числовых параметра. Первый представляет действительную часть, в то время как второй представляет мнимую часть, обозначенную буквой j в буквальном переводе, который вы видели ранее:

>>> complex(3, 2) == 3 + 2j
True

Оба параметра являются необязательными, их значения по умолчанию равны нулю, что упрощает определение комплексных чисел без мнимой части или как действительной, так и мнимой частей:

>>> complex(3) == 3 + 0j
True
>>> complex() == 0 + 0j
True

Версия с одним аргументом может быть полезна при приведении типов. Например, вы можете передать нечисловое значение, такое как строковый литерал, чтобы получить соответствующий объект complex. Обратите внимание, что строка не может содержать никаких пробелов:

>>> complex("3+2j")
(3+2j)

>>> complex("3 + 2j")
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: complex() arg is a malformed string

Позже вы узнаете, как сделать ваши классы совместимыми с этим механизмом приведения типов. Интересно, что когда вы передаете комплексное число в complex(), вы получите тот же экземпляр обратно:

>>> z = complex(3, 2)
>>> z is complex(z)
True

Это согласуется с тем, как работают другие типы чисел в Python, потому что все они неизменяемы. Чтобы создать отдельную копию комплексного числа, вы должны снова вызвать функцию с обоими аргументами или объявить другую переменную с литералом комплексного числа:

>>> z = complex(3, 2)
>>> z is complex(3, 2)
False

Когда вы предоставляете функции два аргумента, они всегда должны быть числами, например int, float, или complex. В противном случае вы получите сообщение об ошибке во время выполнения. Технически говоря,, bool это подкласс int, так что он тоже будет работать:

>>> complex(False, True)  # Booleans, same as complex(0, 1)
1j

>>> complex(3, 2)  # Integers
(3+2j)

>>> complex(3.14, 2.71)  # Floating-point numbers
(3.14+2.71j)

>>> complex("3", "2")  # Strings
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: complex() can't take second arg if first is a string

Все становится еще более странным, когда вы задаете complex() фабричной функции комплексные числа в качестве аргументов. Однако, если вы зададите только первый аргумент, он будет вести себя как прокси-сервер, как и раньше:

>>> complex(complex(3, 2))
(3+2j)

Однако, когда присутствуют два аргумента и хотя бы один из них является комплексным числом, вы получите результаты, которые на первый взгляд может быть трудно объяснить:

>>> complex(1, complex(3, 2))
(-1+3j)

>>> complex(complex(3, 2), 1)
(3+3j)

>>> complex(complex(3, 2), complex(3, 2))
(1+5j)

Чтобы получить ответы, давайте заглянем в строку документации заводской функции или в онлайн-документацию, которая объясняет, что происходит под капотом при вызове complex(real, imag):

Возвращает комплексное число со значением real + imag*1j или преобразует строку или число в комплексное число. (Источник)

В этом пояснении real и imag являются именами аргументов функции. Второй аргумент умножается на мнимую единицу j, и результат добавляется к первому аргументу. Не волнуйтесь, если это все еще не имеет никакого смысла. Вы можете вернуться к этой части, когда прочтете об арифметике комплексных чисел . Правила, с которыми вы ознакомитесь, упростят это.

Когда вы хотели бы использовать фабричную функцию complex() вместо литерала? Это зависит от обстоятельств, но вызов функции может быть более удобным, например, когда вы имеете дело с динамически генерируемыми данными.

Знакомство с комплексными числами Python

В математике комплексные числа - это надмножество действительных чисел, что означает, что каждое действительное число также является комплексным числом, мнимая часть которого равна нулю. Python моделирует эту взаимосвязь с помощью концепции, называемой числовой башней, описанной в PEP 3141:

>>> import numbers
>>> issubclass(numbers.Real, numbers.Complex)
True

Встроенный модуль numbers определяет иерархию числовых типов с помощью абстрактных классов, которые можно использовать для проверки типов и классификации чисел. Например, чтобы определить, принадлежит ли значение к определенному набору чисел, вы можете вызвать isinstance() для него:

>>> isinstance(3.14, numbers.Complex)
True
>>> isinstance(3.14, numbers.Integral)
False

Значение с плавающей запятой 3.14 - это действительное число, которое также является комплексным числом, но не целым. Обратите внимание, что вы не можете напрямую использовать встроенные типы в таком тесте:

>>> isinstance(3.14, complex)
False

Разница между complex и numbers.Complex заключается в том, что они принадлежат к отдельным ветвям дерева иерархии числовых типов, а последний является абстрактным базовым классом без какой-либо реализации:

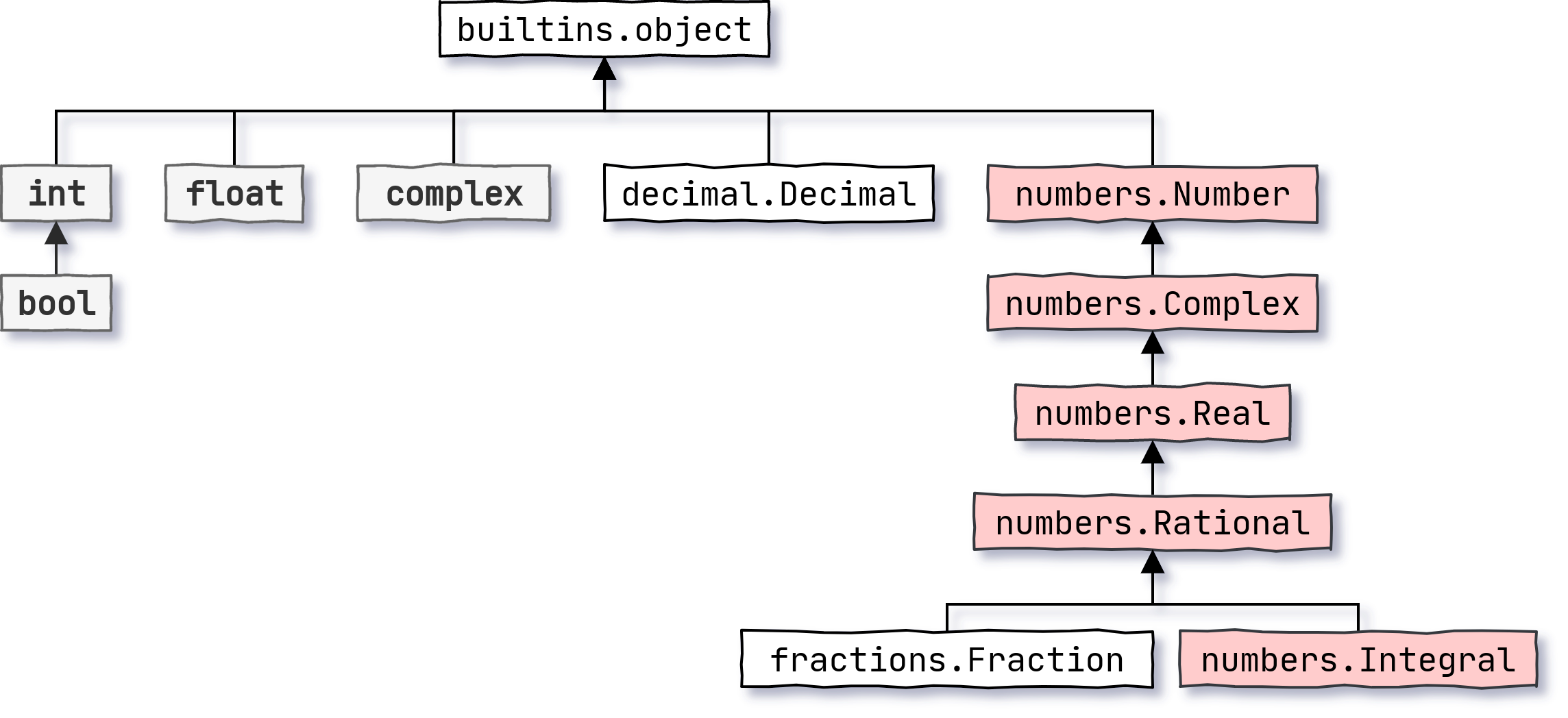Иерархия типов для чисел в Python

Абстрактные базовые классы, которые обозначены красным цветом на диаграмме выше, могут обойти обычный механизм проверки наследования, зарегистрировав несвязанные классы в качестве своих виртуальных подклассов. Вот почему значение с плавающей запятой в примере выглядит как экземпляр numbers.Complex, но не complex.

Доступ к действительной и мнимой частям

Чтобы получить действительную и мнимую части комплексного числа в Python, вы можете воспользоваться соответствующими атрибутами .real и .imag:

>>> z = 3 + 2j
>>> z.real
3.0
>>> z.imag
2.0

Оба свойства доступны только для чтения, поскольку комплексные числа неизменяемы, поэтому попытка присвоить новое значение любому из них завершится неудачей:

>>> z.real = 3.14
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AttributeError: readonly attribute

Поскольку каждое число в Python является более конкретным типом комплексного числа, атрибуты и методы, определенные в numbers.Complex, также доступны для всех числовых типов, включая int и float:

>>> x = 42
>>> x.real
42
>>> x.imag
0

Мнимая часть таких чисел всегда равна нулю.

Вычисление сопряженного комплексного числа

Комплексные числа Python имеют только три открытых члена. Помимо свойств .real и .imag, они предоставляют метод .conjugate(), который переворачивает знак мнимой части:

>>> z = 3 + 2j
>>> z.conjugate()
(3-2j)

Для чисел, мнимая часть которых равна нулю, это не будет иметь никакого эффекта:

>>> x = 3.14
>>> x.conjugate()
3.14

Эта операция сама по себе является обратной, поэтому, выполнив ее дважды, вы получите исходное число, с которого начинали:

>>> z.conjugate().conjugate() == z
True

Хотя это может показаться малозначительным, комплексное сопряжение обладает несколькими полезными арифметическими свойствами, которые, помимо многого другого, могут помочь вычислить деление двух комплексных чисел с помощью ручки и бумаги.

Арифметика комплексных чисел

Поскольку complex является родным типом данных в Python, вы можете вставлять комплексные числа в арифметические выражения и вызывать для них многие встроенные функции. Более продвинутые функции для комплексных чисел определены в модуле cmath, который является частью стандартной библиотеки. Вы познакомитесь с этим в более поздней части этого руководства.

На данный момент, запомнив одно правило, вы сможете применить свои знания по арифметике, полученные в начальной школе, для вычисления основных операций с комплексными числами. Правило, которое следует запомнить, - это определение мнимой единицы, которая удовлетворяет следующему уравнению:

Это выглядит неправильно, когда вы думаете о j как о вещественном числе, но не паникуйте. Если вы проигнорируете это на мгновение и замените каждое вхождение j2 на -1, как если бы оно было константой, то вы получите значение set. Давайте посмотрим, как это работает.

Дополнение

Сумма двух или более комплексных чисел эквивалентна сложению их действительной и мнимой частей по компонентам:

>>> z1 = 2 + 3j
>>> z2 = 4 + 5j
>>> z1 + z2
(6+8j)

Ранее вы узнали, что алгебраические выражения, состоящие из действительных и мнимых чисел, подчиняются стандартным правилам алгебры. Когда вы запишете это алгебраически, вы сможете применить свойство распределения и упростить формулу, разложив на множители и сгруппировав общие термины:

Python автоматически переводит операнды в тип данных complex при добавлении значений смешанных числовых типов:

>>> z = 2 + 3j
>>> z + 7  # Add complex to integer
(9+3j)

Это похоже на неявное преобразование из int в float, с которым вы, возможно, более знакомы.

Вычитание

Вычитание комплексных чисел аналогично их сложению, что означает, что вы также можете применять его поэтапно:

>>> z1 = 2 + 3j
>>> z2 = 4 + 5j
>>> z1 - z2
(-2-2j)

Однако, в отличие от суммы, порядок операндов имеет значение и дает разные результаты, как и в случае с вещественными числами:

>>> z1 + z2 == z2 + z1
True
>>> z1 - z2 == z2 - z1
False

Вы также можете использовать унарный оператор минуса (-) для преобразования комплексного числа в отрицательное значение:

>>> z = 3 + 2j
>>> -z
(-3-2j)

Это инвертирует как действительную, так и мнимую части комплексного числа.

Умножение

Произведение двух или более комплексных чисел становится более интересным:

>>> z1 = 2 + 3j
>>> z2 = 4 + 5j
>>> z1 * z2
(-7+22j)

Как, скажите на милость, у вас получилось получить отрицательное число, состоящее только из положительных чисел? Чтобы ответить на этот вопрос, вы должны вспомнить определение мнимой единицы и переписать выражение в терминах действительной и мнимой частей:

Главное замечание, которое следует сделать, заключается в том, что j умноженное на j дает j2, которое можно заменить на -1. Это меняет знак одного из слагаемых, в то время как остальные правила остаются точно такими же, как и раньше.

Подразделение

Деление комплексных чисел может показаться пугающим на первый взгляд:

>>> z1 = 2 + 3j
>>> z2 = 4 + 5j
>>> z1 / z2
(0.5609756097560976+0.0487804878048781j)

Хотите верьте, хотите нет, но вы можете получить тот же результат, используя только ручку и бумагу! (Хорошо, калькулятор может избавить вас от головной боли в будущем). Когда оба числа выражены в их стандартных формах, хитрость заключается в том, чтобы умножить числитель и знаменатель на сопряженное значение последнего:

Знаменатель преобразуется в квадрат модуля делителя. Подробнее о модуле комплексных чисел вы узнаете позже. Когда вы продолжите выводить формулу, вот что вы получите:

Обратите внимание, что комплексные числа не поддерживают деление на уровни, также известное как целочисленное деление:

>>> z1 // z2
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: can't take floor of complex number.

>>> z1 // 3.14
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: can't take floor of complex number.

Раньше это работало в Python 2.x, но позже было удалено, чтобы избежать двусмысленности.

Возведение в степень

Вы можете возводить комплексные числа в степень, используя двоичный оператор возведения в степень (**) или встроенный pow(), но не тот, который определен в модуле math, который поддерживает только значения с плавающей запятой:

>>> z = 3 + 2j

>>> z**2
(5+12j)

>>> pow(z, 2)
(5+12j)

>>> import math
>>> math.pow(z, 2)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: can't convert complex to float

Как основание, так и показатель степени могут быть любых числовых типов, включая целые, с плавающей запятой, мнимые или комплексные:

>>> 2**z
(1.4676557979464138+7.86422192328995j)

>>> z**2
(5+12j)

>>> z**0.5
(1.8173540210239707+0.5502505227003375j)

>>> z**3j
(-0.13041489185767086-0.11115341486478239j)

>>> z**z
(-5.409738793917679-13.410442370412747j)

Возведение комплексных чисел в степень вручную становится очень сложным, когда они выражаются в их стандартной форме. Гораздо удобнее переписать число в тригонометрической форме и вычислить степень, используя некоторые основы тригонометрии. Если вас интересуют математические выкладки, ознакомьтесь с формулой де Муавра , которая позволяет вам это сделать.

Использование комплексных чисел Python в качестве двумерных векторов

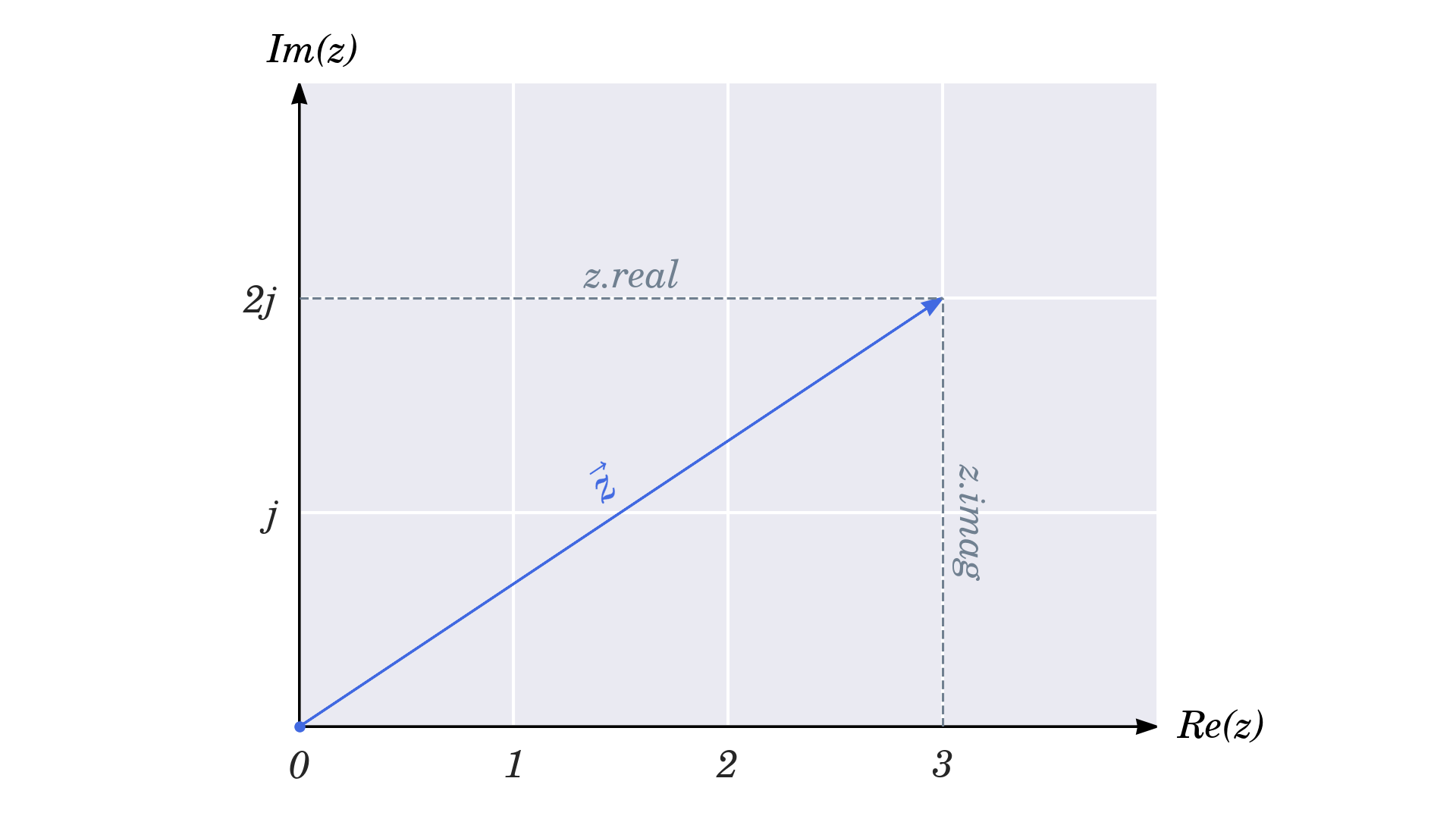
Вы можете визуализировать комплексные числа в виде точек или векторов на евклидовой плоскости в декартовом или прямоугольном виде система координат:

Ось X на комплексной плоскости, также известной как Плоскость Гаусса или Диаграмма Арганда, представляет действительную часть комплексного числа, в то время как ось Y представляет его мнимую часть.

Этот факт приводит к появлению одной из самых крутых функций типа данных complex в Python, которая бесплатно реализует элементарную двумерную векторную. Хотя не все операции в них выполняются одинаково, векторы и комплексные числа имеют много общего.

Получение координат

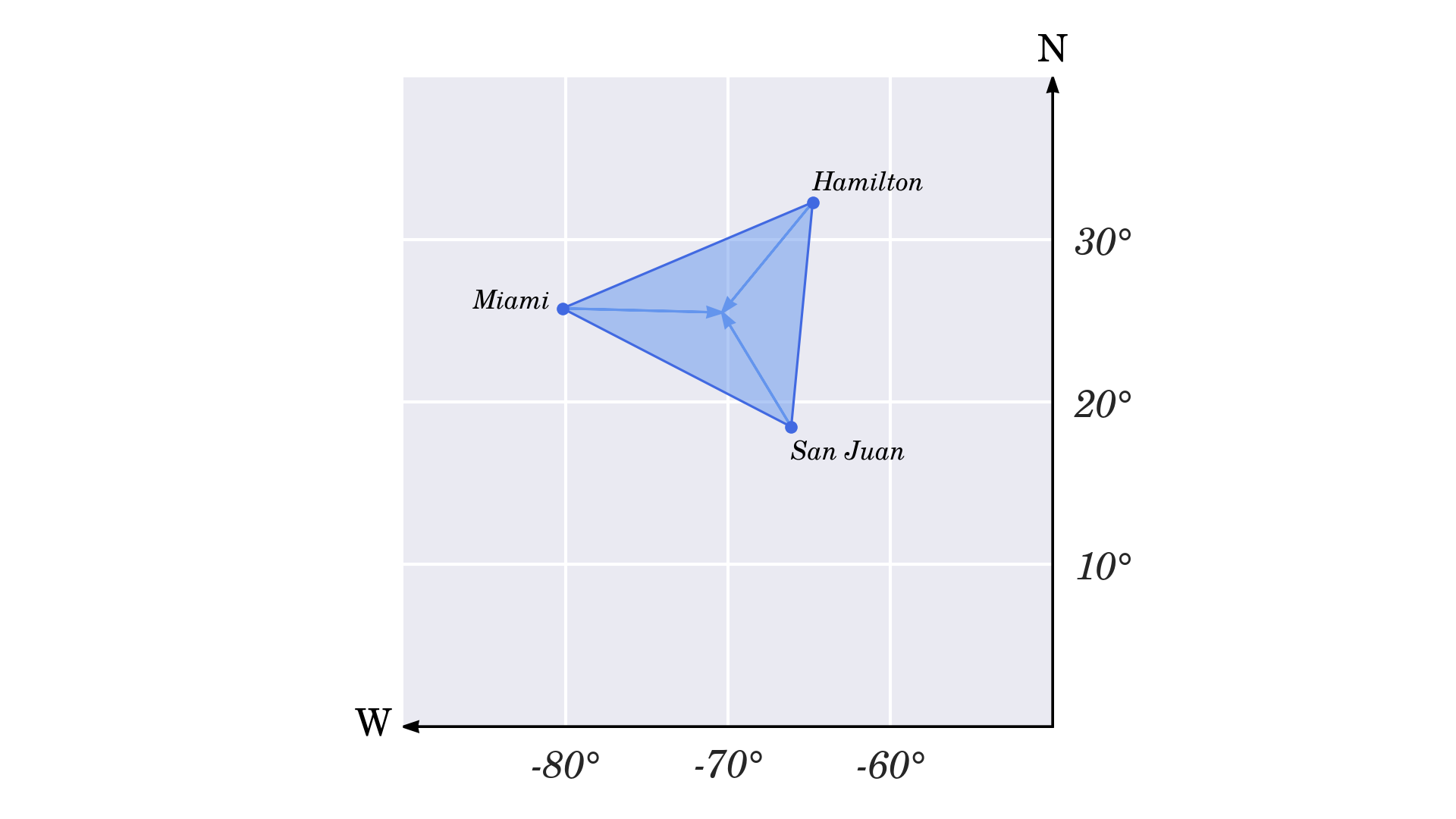
Бермудский треугольник - легендарный регион, известный своими паранормальными явлениями, который охватывает южную оконечность Флориды, Пуэрто-Рико и крошечный остров Бермуды. Его вершины приблизительно обозначены тремя крупными городами, географические координаты которых следующие:

1. Майами: 25° 45’ 42.054” Северная широта, 80° 11’ 30.438” с.ш.
2. Сан-Хуан: 18° 27’ 58.8” Северная широта, 66° 6’ 20.598” с.ш.
3. Гамильтон: 32° 17’ 41.64” Северная широта, 64° 46’ 58.908” с.ш.

После преобразования этих координат в десятичные градусы вы получите два числа с плавающей запятой для каждого города. Вы можете использовать тип данных complex для хранения упорядоченных пар чисел. Поскольку широта - это вертикальная координата, а долгота - горизонтальная, возможно, было бы удобнее переключать их, следуя традиционному порядку декартовой системы координат. координаты:

miami_fl = complex(-80.191788, 25.761681)
san_juan = complex(-66.105721, 18.466333)
hamilton = complex(-64.78303, 32.2949)

Отрицательные значения долготы соответствуют западному полушарию, в то время как положительные значения широты соответствуют северному полушарию.

Имейте в виду, что это сферические координаты. Чтобы правильно спроецировать их на плоскую поверхность, вам необходимо учитывать кривизну Земли. Одной из первых картографических проекций, использованных в картографии, была проекция Меркатора, которая помогала морякам ориентироваться на своих кораблях. Но давайте проигнорируем все это и предположим, что значения уже выражены в прямоугольной системе координат.

Когда вы нанесете числа на комплексную плоскость, вы получите приблизительное изображение Бермудского треугольника:

В сопутствующих материалах вы найдете интерактивную Записную книжку Jupyter, которая отображает Бермудский треугольник с помощью библиотеки Matplotlib. Чтобы загрузить исходный код и материалы для этого руководства, перейдите по ссылке ниже:

Получите пример кода: Нажмите здесь, чтобы получить пример кода, который вы будете использовать для изучения комплексных чисел в Python в этом руководстве.

Если вам не нравится вызов заводской функции complex(), вы можете создать псевдоним типа с более подходящим именем или использовать буквенную форму комплексного числа, чтобы сохраните несколько нажатий клавиш:

CityCoordinates = complex
miami_fl = CityCoordinates(-80.191788, 25.761681)
miami_fl = -80.191788 + 25.761681j

Если вам нужно было добавить больше атрибутов к городу, вы могли бы использовать именованный кортеж или класс данных или создать пользовательский класс.

Вычисление магнитуды

Величина , также известная как модуль или радиус комплексное число - это длина вектора, который изображает его на комплексной плоскости:

Вы можете вычислить это из теоремы Пифагора, извлекая квадратный корень из суммы возведенной в квадрат действительной части и возведенной в квадрат мнимой части:

Можно подумать, что Python позволит вам вычислить длину такого вектора с помощью встроенного len(), но это не так. Чтобы получить величину комплексного числа, вы должны вызвать другую глобальную функцию с именем abs(),, которая обычно используется для вычисления абсолютного значения числа:

>>> len(3 + 2j)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: object of type 'complex' has no len()

>>> abs(3 + 2j)
3.605551275463989

Эта функция удаляет знак из целых чисел, которые вы вводите, но для комплексных чисел она возвращает величину или длину вектора:

>>> abs(-42)
42

>>> z = 3 + 2j

>>> abs(z)
3.605551275463989

>>> from math import sqrt
>>> sqrt(z.real**2 + z.imag**2)
3.605551275463989

Возможно, вы помните из предыдущего раздела, что комплексное число, умноженное на сопряженное с ним, дает квадрат его величины.

Нахождение расстояния между двумя точками

Давайте найдем геометрический центр Бермудского треугольника и расстояния до него от трех городов, образующих его границы. Сначала вам нужно просуммировать все координаты и разделить результат на их количество, чтобы получить среднее значение:

geometric_center = sum([miami_fl, san_juan, hamilton]) / 3

Это даст вам точку, расположенную в Атлантическом океане, где-то внутри треугольника:

Теперь вы можете создавать векторы, привязанные к городам и направленные к геометрическому центру треугольника. Векторы создаются путем вычитания источника из целевой точки:

v1 = geometric_center - miami_fl
v2 = geometric_center - san_juan
v3 = geometric_center - hamilton

Поскольку вы вычитаете комплексные числа, каждый вектор также является комплексным числом, состоящим из двух частей. Чтобы определить расстояния, вычислите величину каждого вектора:

>>> abs(v1)
9.83488994681275

>>> abs(v2)
8.226809506084367

>>> abs(v3)
8.784732429678444

Эти длины векторов не отражают значимых расстояний, но являются хорошим приближением для игрушечного примера, подобного этому. Чтобы представить точные результаты в осязаемых единицах, вам пришлось бы сначала преобразовать координаты из сферических в прямоугольные или рассчитать расстояние, используя вместо этого метод большой окружности.

Перевод, переворачивание, масштабирование и поворот

Возможно, вас беспокоит, что треугольник находится во втором квадранте декартовой системы координат. Давайте переместим его так, чтобы его геометрический центр совпал с началом координат. Все три вершины будут переведены на длину вектора, указанного геометрическим центром, но в противоположном направлении:

triangle = miami_fl, san_juan, hamilton
offset = -geometric_center
centered_triangle = [vertex + offset for vertex in triangle]

Обратите внимание, что вы складываете два комплексных числа вместе, что приводит к их поэлементному сложению. Это аффинное преобразование, поскольку оно не изменяет форму треугольника или взаимное расположение его вершин:

Зеркальное отражение треугольника вокруг действительной или мнимой оси требует инвертирования соответствующей составляющей в его вершинах. Например, чтобы перевернуть по горизонтали, вам придется использовать отрицательную часть действительной части, которая соответствует горизонтальному направлению. Чтобы перевернуть его вертикально, вы возьмете отрицательную часть мнимой части:

flipped_horizontally = [complex(-v.real, v.imag) for v in centered_triangle]
flipped_vertically = [complex(v.real, -v.imag) for v in centered_triangle]

Последнее, по сути, то же самое, что вычисление сопряженного комплексного числа, поэтому вы можете вызвать .conjugate() непосредственно для каждой вершины, чтобы выполнить тяжелую работу за вас:

flipped_vertically = [v.conjugate() for v in centered_triangle]

Естественно, ничто не мешает вам применить симметрию в любом направлении или в обоих направлениях одновременно. В таком случае вы можете использовать унарный оператор минус перед комплексным числом, чтобы перевернуть его действительную и мнимую части:

flipped_in_both_directions = [-v for v in centered_triangle]

Попробуйте различные комбинации переворотов с помощью интерактивного блокнота Jupyter, доступного в загружаемых материалах. Вот как будет выглядеть треугольник, если вы перевернете его вдоль обеих осей:

Масштабирование аналогично переводу, но вместо добавления смещения вы собираетесь умножить каждую вершину на постоянный коэффициент, который должен быть действительным число:

scaled_triangle = [1.5*vertex for vertex in centered_triangle]

В результате оба компонента каждого комплексного числа будут умножены на одинаковую величину. Это должно растянуть ваш Бермудский треугольник, чтобы он выглядел больше на графике:

Умножение вершин треугольника на другое комплексное число, с другой стороны, приводит к вращению треугольника вокруг системы координатего происхождение. Это сильно отличается от того, как вы обычно умножаете векторы друг на друга. Например, скалярное произведение двух векторов даст скаляр, в то время как их перекрестное произведение возвращает новый вектор в трехмерном пространстве, который перпендикулярен к поверхности, которую они определяют.

Примечание: Произведение двух комплексных чисел не представляет собой векторное умножение. Вместо этого он определяется как матричное умножение в двумерном векторном пространстве, с 1 и j в качестве стандартной основы. Умножаем (x₁ + y₁j на (x₂ + y₂j) соответствует следующему матричному умножению:

Это матрица вращения слева, благодаря которой математика работает просто отлично.

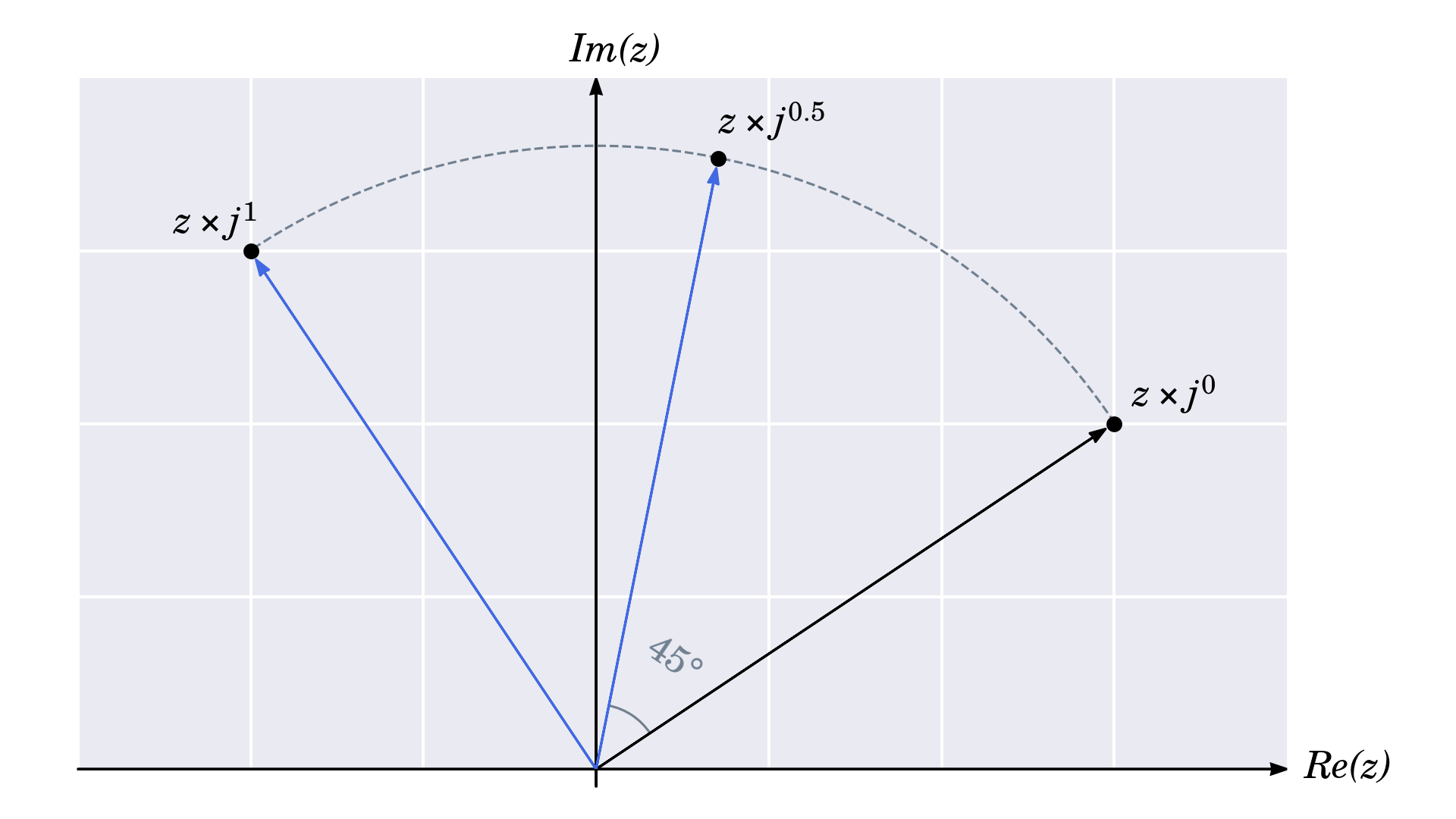
Когда вы умножите вершины на воображаемую единицу, треугольник повернется на 90° против часовой стрелки. Если вы будете продолжать повторять это, то в конечном итоге придете к тому, с чего начали:

Как найти конкретное комплексное число, которое повернет другое комплексное число на любой желаемый угол при умножении обоих? Сначала взгляните на следующую таблицу, в которой приведены последовательные повороты на 90°:

90° rotations	Total angle	Formula	Exponent	Value
0	0°	z	j0	1
1	90°	z × j	j1	j
2	180°	z × j × j	j2	-1
3	270°	z × j × j × j	j3	-j
4	360°	z × j × j × j × j	j4	1
5	450°	z × j × j × j × j × j	j5	j
6	540°	z × j × j × j × j × j × j	j6	-1
7	630°	z × j × j × j × j × j × j × j	j7	-j
8	720°	z × j × j × j × j × j × j × j × j	j8	1

Когда вы выражаете повторное умножение на j в виде целых положительных показателей, возникает закономерность. Обратите внимание, что при возведении мнимой единицы в последующие степени происходит многократное повторение одних и тех же значений. Вы можете экстраполировать это на дробные показатели и ожидать, что они будут соответствовать промежуточным углам.

Например, показатель степени в середине первого оборота равен 0,5 и представляет угол в 45°:

Итак, если вы знаете, что степень единицы представляет собой прямой угол, а все, что находится между ними, пропорционально масштабируется, то вы можете вывести эту общую формулу для произвольных поворотов:

def rotate(z: complex, degrees: float) -> complex:
    return z * 1j**(degrees/90)

Обратите внимание, что вращение становится более естественным, когда вы выражаете свои комплексные числа в полярных координатах, которые уже описывают угол. Затем вы можете воспользоваться экспоненциальной формой, чтобы упростить вычисления:

 

Существует два способа поворота числа с использованием полярных координат:

import math, cmath

def rotate1(z: complex, degrees: float) -> complex:
    radius, angle = cmath.polar(z)
    return cmath.rect(radius, angle + math.radians(degrees))

def rotate2(z: complex, degrees: float) -> complex:
    return z * cmath.rect(1, math.radians(degrees))

Вы можете суммировать углы или умножить комплексное число на единичный вектор.

Вы узнаете о них больше в следующем разделе.

Изучение математического модуля для комплексных чисел: cmath

Вы уже видели, что некоторые встроенные функции, такие как abs() и pow(), принимают комплексные числа, в то время как другие - нет. Например, вы не можете использовать round() комплексное число, потому что такая операция не имеет смысла:

>>> round(3 + 2j)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: type complex doesn't define __round__ method

Многие расширенные математические функции, такие как тригонометрические, гиперболические или логарифмические доступны в стандартной библиотеке. К сожалению, даже если вы знаете все о модуле Python math, это не поможет, потому что ни одна из его функций не поддерживает комплексные числа. Вам нужно будет объединить его с модулем cmath, который определяет соответствующие функции для комплексных чисел.

Модуль cmath переопределяет все константы с плавающей запятой из math, чтобы они были у вас под рукой без необходимости импортировать оба модуля:

>>> import math, cmath
>>> for name in "e", "pi", "tau", "nan", "inf":
...     print(name, getattr(math, name) == getattr(cmath, name))
...
e True
pi True
tau True
nan False
inf True

Обратите внимание, что nan - это особое значение, которое никогда не равно ничему другому, включая само себя! Вот почему вы видите одиночное значение False в выходных данных выше. В дополнение к этому, cmath предоставляет два сложных аналога для NaN (не число) и infinity, причем оба имеют нулевые действительные части:

>>> from cmath import nanj, infj
>>> nanj.real, nanj.imag
(0.0, nan)
>>> infj.real, infj.imag
(0.0, inf)

В cmath примерно вдвое меньше функций, чем в стандартном модуле math. Большинство из них имитируют исходное поведение, но некоторые из них уникальны для комплексных чисел. Они позволят вам выполнить преобразование между двумя системами координат, которое вы изучите в этом разделе.

Извлечение корня из комплексного числа

Фундаментальная теорема алгебры гласит, что многочлен степени n с комплексными коэффициентами имеет ровно n сложные корни. Это весьма важно, если вы задумаетесь об этом, так что дайте этому время на размышление.

Теперь давайте возьмем в качестве примера квадратичную функцию x² + 1. Визуально эта парабола не пересекает ось X, поскольку она находится на одну единицу выше начала координат. Дискриминант функции отрицательный, что подтверждает это наблюдение арифметически. В то же время, это многочлен второй степени, поэтому у него должно быть два комплексных корня, даже если у него нет действительных корней!

Чтобы найти эти корни, вы можете переписать функцию в виде квадратного уравнения, затем переместить константу вправо и извлечь квадратный корень из обеих частей:

В области действительных чисел квадратный корень определен только для неотрицательных входных значений. Следовательно, вызов этой функции в Python вызовет исключение с соответствующим сообщением об ошибке:

>>> import math
>>> math.sqrt(-1)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: math domain error

Однако, если вы вместо этого будете рассматривать √-1 как комплексное число и вызовете соответствующую функцию из модуля cmath, то получите более значимый результат:

>>> import cmath
>>> cmath.sqrt(-1)
1j

В этом есть смысл. В конце концов, промежуточная форма x² = -1 квадратного уравнения является самим определением мнимой единицы. Но, подождите минутку. Куда делся другой комплексный корень? А как насчет комплексных корней многочленов более высокой степени?

Например, многочлен четвертой степени x⁴ + 1, который может быть записан в виде уравнения x⁴ = -1, имеет следующие четыре сложных корня:

• z₀ = -√2/2 + √2/2j
• z₁ = -√2/2 - √2/2j
• z₂ = √2/2 + √2/2j
• z₃ = √2/2 - √2/2j

Возведение каждого корня в четвертую степень дает комплексное число, равное -1 + 0j или действительное число -1:

>>> import cmath
>>> z0 = -cmath.sqrt(2)/2 + cmath.sqrt(2)/2*1j

>>> z0**4
(-1.0000000000000004-0j)

>>> (z0**4).real
-1.0000000000000004

Вы заметите, что результирующее значение не совсем равно -1 из-за ошибки округления в арифметике с плавающей запятой. Чтобы учесть это, вы можете вызывать cmath.isclose() всякий раз, когда вам нужно определить, близки ли два комплексных числа по значению:

>>> cmath.isclose(z0**4, -1)
True

К сожалению, вы не можете вычислить другие сложные корни с помощью чистого Python, потому что регулярное возведение в степень всегда дает одно решение:

>>> pow(-1, 1/4)
(0.7071067811865476+0.7071067811865475j)

Это только один из перечисленных ранее корней. Математическая формула для нахождения всех комплексных корней использует тригонометрическую форму комплексных чисел:

r и φ являются полярными координатами комплексного числа, в то время как n - степень многочлена, а k - индекс корня, начинающийся с нуля. Хорошей новостью является то, что вам не нужно кропотливо вычислять эти корни самостоятельно. Самый быстрый способ найти их - это установить стороннюю библиотеку, такую как NumPy и импортировать это для вашего проекта:

>>> import numpy as np
>>> np.roots([1, 0, 0, 0, 1])  # Coefficients of the polynomial x**4 + 1
array([-0.70710678+0.70710678j, -0.70710678-0.70710678j,
        0.70710678+0.70710678j,  0.70710678-0.70710678j])

Знание различных форм комплексных чисел и их систем координат может оказаться полезным. Как вы можете видеть, это помогает в решении практических задач, таких как поиск комплексных корней. Итак, в следующем разделе вы познакомитесь с более подробной информацией.

Преобразование между прямоугольными и полярными координатами

С геометрической точки зрения комплексное число можно рассматривать двояко. С одной стороны, это точка, расстояние от которой по горизонтали и вертикали до начала координат однозначно определяет ее местоположение. Они известны как прямоугольные координаты, состоящие из действительной и мнимой частей.

С другой стороны, вы можете описать ту же точку в полярных координатах, что также позволит вам однозначно найти ее на двух расстояниях:

1. Радиальное расстояние - это длина радиуса, измеренная от начала координат.
2. Угловое расстояние - это угол, измеренный между горизонтальной осью и радиусом.

Радиус, также известный как модуль, соответствует величине комплексного числа или длине вектора. Угол обычно называют фазой или аргументом комплексного числа. При работе с тригонометрическими функциями полезно выражать угол в радианах, а не в градусах.

Вот изображение комплексного числа в обеих системах координат:

Следовательно, точка (3, 2) в декартовой системе координат имеет радиус приблизительно 3,6 и угол около 33,7°, или примерно π более 5,4 радиан.

Преобразование между двумя системами координат стало возможным благодаря нескольким функциям, встроенным в модуль cmath. В частности, чтобы получить полярные координаты комплексного числа, вы должны передать его в cmath.polar():

>>> import cmath
>>> cmath.polar(3 + 2j)
(3.605551275463989, 0.5880026035475675)

Он вернет кортеж, где первый элемент - это радиус, а второй элемент - угол в радианах. Обратите внимание, что радиус имеет то же значение, что и магнитуда, которую вы можете вычислить, вызвав abs() для вашего комплексного числа. И наоборот, если бы вас интересовало только определение угла наклона комплексного числа, то вы могли бы вызвать cmath.phase():

>>> z = 3 + 2j

>>> abs(z)  # Magnitude is also the radial distance
3.605551275463989

>>> import cmath
>>> cmath.phase(3 + 2j)
0.5880026035475675

>>> cmath.polar(z) == (abs(z), cmath.phase(z))
True

Угол может быть получен с помощью базовой тригонометрии, поскольку действительная часть, мнимая часть и величина вместе образуют прямоугольный треугольник:

Вы можете использовать обратные тригонометрические функции, такие как арксинус, либо из math, либо из cmath, но последние будут выдавать комплексные значения с мнимая часть, равная нулю:

>>> z = 3 + 2j

>>> import math
>>> math.acos(z.real / abs(z))
0.5880026035475675
>>> math.asin(z.imag / abs(z))
0.5880026035475676
>>> math.atan(z.imag / z.real)  # Prefer math.atan2(z.imag, z.real)
0.5880026035475675

>>> import cmath
>>> cmath.acos(z.real / abs(z))
(0.5880026035475675-0j)

Однако при использовании функции арктангенс следует быть осторожным с одной маленькой деталью, которая побудила многие языки программирования разработать альтернативную реализацию, называемую atan2(). Вычисление соотношения между мнимой и действительной частью иногда может привести к сингулярности, например, из-за деления на ноль. Более того, при этом теряются отдельные признаки двух величин, что делает невозможным точное определение угла:

>>> import math

>>> math.atan(1 / 0)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ZeroDivisionError: division by zero

>>> math.atan2(1, 0)
1.5707963267948966

>>> math.atan(1 / 1) == math.atan(-1 / -1)
True

>>> math.atan2(1, 1) == math.atan2(-1, -1)
False

Обратите внимание, что atan() не удается распознать две разные точки, расположенные в противоположных квадрантах системы координат. С другой стороны, atan2() ожидает, что два аргумента вместо одного сохранят отдельные знаки перед разделением одного на другой, и позволяет избежать других проблем.

Чтобы получить градусы вместо радиан, вы можете снова выполнить необходимое преобразование, используя модуль math:

>>> import math
>>> math.degrees(0.5880026035475675)  # Radians to degrees
33.690067525979785
>>> math.radians(180)  # Degrees to radians
3.141592653589793

Обращение процесса вспять, то есть преобразование полярных координат в прямоугольные, зависит от другой функции. Однако вы не можете просто передать тот же кортеж, который вы получили из cmath.polar(), поскольку cmath.rect() ожидает два отдельных аргумента:

>>> cmath.rect(cmath.polar(3 + 2j))
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: rect expected 2 arguments, got 1

При выполнении задания рекомендуется сначала распаковать кортеж и присвоить этим элементам более наглядные имена. Теперь вы можете правильно вызывать cmath.rect():

>>> radius, angle = cmath.polar(3 + 2j)
>>> cmath.rect(radius, angle)
(3+1.9999999999999996j)

При выполнении вычислений в Python могут возникнуть ошибки округления. За кулисами Python вызывает тригонометрические функции для получения действительной и мнимой частей:

>>> import math
>>> radius*(math.cos(angle) + math.sin(angle)*1j)
(3+1.9999999999999996j)

>>> import cmath
>>> radius*(cmath.cos(angle) + cmath.sin(angle)*1j)
(3+1.9999999999999996j)

Опять же, в этом случае не имеет значения, используете ли вы math или cmath, поскольку результаты будут идентичными.

Различные представления комплексных чисел

Независимо от системы координат, одно и то же комплексное число можно выразить в нескольких математически эквивалентных формах:

• Алгебраический (стандартный)
• Геометрический
• Тригонометрический
• Экспоненциальный

Этот список не является исчерпывающим, поскольку существует больше представлений, таких как матричное представление комплексных чисел.

Возможность выбора позволяет выбрать наиболее удобный вариант для решения данной задачи. Например, вам понадобится экспоненциальная форма для вычисления дискретного преобразования Фурье в следующем разделе. Использование этой формы также подходит для умножения и деления комплексных чисел.

Вот краткое описание отдельных форм комплексных чисел и их координат:

Form	Rectangular	Polar
Algebraic	z = x + yj	-
Geometric	z = (x, y)	z = (r, φ)
Trigonometric	z = |z|(cos(x/|z|) + jsin(y/|z|))	z = r(cos(φ) + jsin(φ))
Exponential	z = |z|eatan2(y/x)j	z = r(ejφ)

Алгебраическая форма является родной для Python, когда вы указываете комплексные числа, используя их литералы. Вы также можете рассматривать их как точки на евклидовой плоскости в декартовой или полярной системах координат. Хотя в Python нет отдельных представлений для тригонометрической или экспоненциальной формы, вы можете проверить, верны ли математические принципы.

Например, приведение формулы Эйлера к тригонометрической форме преобразует ее в экспоненциальную. Вы можете либо вызвать cmath модуля exp(), либо повысить константу e до степени, чтобы получить тот же результат:

>>> import cmath

>>> algebraic = 3 + 2j
>>> geometric = complex(3, 2)
>>> radius, angle = cmath.polar(algebraic)
>>> trigonometric = radius * (cmath.cos(angle) + 1j*cmath.sin(angle))
>>> exponential = radius * cmath.exp(1j*angle)

>>> for number in algebraic, geometric, trigonometric, exponential:
...     print(format(number, "g"))
...
3+2j
3+2j
3+2j
3+2j

Все формы действительно представляют собой разные способы кодирования одного и того же числа. Однако вы не можете сравнить их напрямую из-за ошибок округления, которые могут возникнуть при этом. Используйте cmath.isclose() для безопасного сравнения или format() соответствующим образом используйте числа в виде строк. Как форматировать такие строки, вы узнаете в следующем разделе.

Объяснение того, почему различные формы комплексного числа эквивалентны, требует математического анализа и выходит далеко за рамки данного руководства. Однако, если вы интересуетесь математикой, то вы найдете увлекательными связи между различными областями математики, которые проявляются с помощью комплексных чисел.

Разбор комплексного числа в Python

Вы уже многое узнали о комплексных числах Python и ознакомились с предварительными примерами. Однако, прежде чем двигаться дальше, стоит затронуть несколько заключительных тем. В этом разделе вы познакомитесь с сравнением комплексных чисел, форматированием строк, которые их содержат, и многим другим.

Проверка равенства комплексных чисел

Математически два комплексных числа равны, если они имеют одинаковые значения независимо от принятой системы координат. Однако преобразование полярных и прямоугольных координат в Python обычно приводит к ошибкам округления, поэтому при их сравнении вам нужно обращать внимание на незначительные различия.

Например, когда вы рассматриваете точку на единичной окружности, радиус которой равен единице и наклонен на 60°, тригонометрия работает отлично, и преобразование выполняется с помощью ручки и бумаги прямолинейно:

>>> import math, cmath

>>> z1 = cmath.rect(1, math.radians(60))
>>> z2 = complex(0.5, math.sqrt(3)/2)

>>> z1 == z2
False

>>> z1.real, z2.real
(0.5000000000000001, 0.5)
>>> z1.imag, z2.imag
(0.8660254037844386, 0.8660254037844386)

Даже если вы знаете, что z1 и z2 - это одна и та же точка, Python не может определить это из-за ошибок округления. К счастью, в документе PEP 485 определены функции для обеспечения приблизительного равенства, которые доступны в модулях math и cmath:

>>> math.isclose(z1.real, z2.real)
True

>>> cmath.isclose(z1, z2)
True

Не забывайте всегда использовать их при сравнении комплексных чисел! Если допустимое отклонение по умолчанию недостаточно для ваших вычислений, вы можете изменить его, указав дополнительные аргументы.

Порядок следования комплексных чисел

Если вы знакомы с кортежами, то знаете, что Python может сортировать их следующим образом:

>>> planets = [
...     (6, "saturn"),
...     (4, "mars"),
...     (1, "mercury"),
...     (5, "jupiter"),
...     (8, "neptune"),
...     (3, "earth"),
...     (7, "uranus"),
...     (2, "venus"),
... ]
>>> from pprint import pprint
>>> pprint(sorted(planets))
[(1, 'mercury'),
 (2, 'venus'),
 (3, 'earth'),
 (4, 'mars'),
 (5, 'jupiter'),
 (6, 'saturn'),
 (7, 'uranus'),
 (8, 'neptune')]

По умолчанию отдельные кортежи сравниваются слева направо:

>>> (6, "saturn") < (4, "mars")
False
>>> (3, "earth") < (3, "moon")
True

В первом случае число 6 больше, чем 4, поэтому названия планет вообще не учитываются. Однако они могут помочь разрешить спор. Однако это не относится к комплексным числам, поскольку они не определяют естественное отношение упорядочения. Например, вы получите сообщение об ошибке, если попытаетесь сравнить два комплексных числа:

>>> (3 + 2j) < (2 + 3j)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: '<' not supported between instances of 'complex' and 'complex'

Должно ли воображаемое измерение иметь больший вес, чем реальное? Следует ли сравнивать их величины? Решать вам, и ответы будут разными. Поскольку вы не можете сравнивать комплексные числа напрямую, вам нужно указать Python, как их сортировать, указав пользовательскую ключевую функцию , например abs():

>>> cities = {
...     complex(-64.78303, 32.2949): "Hamilton",
...     complex(-66.105721, 18.466333): "San Juan",
...     complex(-80.191788, 25.761681): "Miami"
... }

>>> for city in sorted(cities, key=abs, reverse=True):
...     print(abs(city), cities[city])
...
84.22818453809096 Miami
72.38647347392259 Hamilton
68.63651945864338 San Juan

Это позволит отсортировать комплексные числа по их величине в порядке убывания.

Форматирование комплексных чисел в виде строк

Не существует никаких кодов форматирования, специфичных для комплексных чисел, но вы можете отформатировать их действительную и мнимую части отдельно, используя стандартные коды для чисел с плавающей запятой. Ниже вы найдете несколько методов, которые это демонстрируют. Некоторые из них позволят применить ваш спецификатор формата как к действительной, так и к мнимой частям одновременно.

Примечание: Форматирование строки может позволить вам игнорировать ошибку представления с плавающей запятой и притвориться, что ее не существует:

>>> import cmath
>>> z = abs(3 + 2j) * cmath.exp(1j*cmath.phase(3 + 2j))

>>> str(z)
'(3+1.9999999999999996j)'

>>> format(z, "g")
'3+2j'

Буква "g" в указателе формата означает общий формат, который округляет ваше число до требуемой точности. Точность по умолчанию равна шести значащим цифрам.

Давайте возьмем в качестве примера следующее комплексное число и отформатируем его с двумя знаками после запятой в обеих частях:

>>> z = pow(3 + 2j, 0.5)
>>> print(z)
(1.8173540210239707+0.5502505227003375j)

Быстрый способ сделать это - либо вызвать format() с помощью спецификатора числового формата, либо создать соответствующим образом отформатированную f-строку:

>>> format(z, ".2f")
'1.82+0.55j'

>>> f"{z:.2f}"
'1.82+0.55j'

Если вам нужно больше контроля, например, добавить дополнительное заполнение вокруг оператора plus, то f-строка будет лучшим выбором:

>>> f"{z.real:.2f} + {z.imag:.2f}j"
'1.82 + 0.55j'

Вы также можете вызвать .format() для объекта string и передать позиционный или аргументы ключевого слова к нему:

>>> "{0:.2f} + {0:.2f}j".format(z.real, z.imag)
'1.82 + 1.82j'

>>> "{re:.2f} + {im:.2f}j".format(re=z.real, im=z.imag)
'1.82 + 0.55j'

Позиционные аргументы предоставляют последовательность значений, в то время как аргументы с ключевыми словами позволяют обращаться к ним по имени. Аналогично, вы можете использовать оператор строки по модулю (%) либо с кортежем, либо со словарем :

>>> "%.2f + %.2fj" % (z.real, z.imag)
'1.82 + 0.55j'

>>> "%(re).2f + %(im).2fj" % {"re": z.real, "im": z.imag}
'1.82 + 0.55j'

Однако здесь используется другой синтаксис заполнителя и он немного старомоден.

Создание собственного сложного типа данных

Модель данных Python определяет набор специальных методов, которые вы можете реализовать, чтобы сделать ваши классы совместимыми с определенными встроенными типами. Допустим, вы работали с точками и векторами и хотели получить угол между двумя связанными векторами. Вы могли бы рассчитать их скалярное произведение и выполнить некоторую тригонометрию. В качестве альтернативы вы можете воспользоваться комплексными числами.

Давайте сначала определим ваши классы:

from typing import NamedTuple

class Point(NamedTuple):
    x: float
    y: float

class Vector(NamedTuple):
    start: Point
    end: Point

Точка Point имеет координаты x и y, в то время как точка Vector соединяет две точки. Возможно, вы помните cmath.phase(), который вычисляет угловое расстояние для комплексного числа. Итак, если бы вы рассматривали свои векторы как комплексные числа и знали их фазы, то могли бы вычесть их, чтобы получить желаемый угол.

Чтобы заставить Python распознавать экземпляры vector как комплексные числа, вы должны указать .__complex__() в теле класса:

class Vector(NamedTuple):
    start: Point
    end: Point

    def __complex__(self):
        real = self.end.x - self.start.x
        imag = self.end.y - self.start.y
        return complex(real, imag)

Код внутри всегда должен возвращать экземпляр типа данных complex, поэтому обычно он создает новое комплексное число из вашего объекта. Здесь вы вычитаете начальную и конечную точки, чтобы получить горизонтальное и вертикальное смещения, которые служат действительной и мнимой частями. Метод будет выполняться через делегирование при вызове глобального complex() для экземпляра vector:

>>> vector = Vector(Point(-2, -1), Point(1, 1))
>>> complex(vector)
(3+2j)

В некоторых случаях вам не обязательно выполнять такое приведение типов самостоятельно. Давайте рассмотрим пример на практике:

>>> v1 = Vector(Point(-2, -1), Point(1, 1))
>>> v2 = Vector(Point(10, -4), Point(8, -1))

>>> import math, cmath
>>> math.degrees(cmath.phase(v2) - cmath.phase(v1))
90.0

У вас есть два вектора, обозначенных четырьмя различными точками. Затем вы передаете их непосредственно в cmath.phase(), который преобразует их в комплексное число и возвращает фазу. Разность фаз - это угол между двумя векторами.

Разве это не прекрасно? Вы избавили себя от необходимости вводить много кода, подверженного ошибкам, используя комплексные числа и немного магии Python.

Вычисление дискретного преобразования Фурье с комплексными числами

Хотя вы можете использовать действительные числа для вычисления коэффициентов синуса и косинуса частот периодической функции с помощью Преобразования Фурье, обычно удобнее иметь дело только с одним комплексным коэффициентом на частоту. Дискретное преобразование Фурье в комплексной области задается следующей формулой:

Для каждого частотного диапазона k измеряется корреляция сигнала и конкретной синусоидальной волны, выраженная в виде комплексного числа в экспоненциальной форме . (Спасибо тебе, Леонард Эйлер!) угловая частота волны может быть вычислена путем умножения круглого угла, который равен 2π радианам, на k на количество дискретных отсчетов:

Это кодирование на Python выглядит довольно аккуратно, если использовать тип данных complex:

from cmath import pi, exp

def discrete_fourier_transform(x, k):
    omega = 2 * pi * k / (N := len(x))
    return sum(x[n] * exp(-1j * omega * n) for n in range(N))

Эта функция является буквальной транскрипцией приведенных выше формул. Теперь вы можете выполнить частотный анализ звука, который вы загружаете из аудиофайла с помощью модуля Python wave или который вы синтезируете с нуля. Один из блокнотов Jupyter, прилагаемых к этому руководству, позволяет вам в интерактивном режиме выполнять синтез и анализ звука.

Чтобы построить частотный спектр с помощью Matplotlib, вы должны знать частоту дискретизации, которая определяет ваше разрешение частотного диапазона, а также Предел Найквиста:

import matplotlib.pyplot as plt

def plot_frequency_spectrum(
    samples,
    samples_per_second,
    min_frequency=0,
    max_frequency=None,
):
    num_bins = len(samples) // 2
    nyquist_frequency = samples_per_second // 2

    magnitudes = []
    for k in range(num_bins):
        magnitudes.append(abs(discrete_fourier_transform(samples, k)))

    # Normalize magnitudes
    magnitudes = [m / max(magnitudes) for m in magnitudes]

    # Calculate frequency bins
    bin_resolution = samples_per_second / len(samples)
    frequency_bins = [k * bin_resolution for k in range(num_bins)]

    plt.xlim(min_frequency, max_frequency or nyquist_frequency)
    plt.bar(frequency_bins, magnitudes, width=bin_resolution)

Количество частотных интервалов в спектре равно половине отсчетов, в то время как частота Найквиста ограничивает максимальную частоту, которую вы можете измерить. Преобразование возвращает комплексное число, величина которого соответствует амплитуде синусоидальной волны на заданной частоте, а ее угол равен фазе.

Примечание: Чтобы получить правильные значения амплитуды, вы должны удвоить это число и разделить полученную величину на количество выборок. С другой стороны, если вас интересует только частотная гистограмма, то вы можете нормализовать значения по их сумме или максимальной частоте.

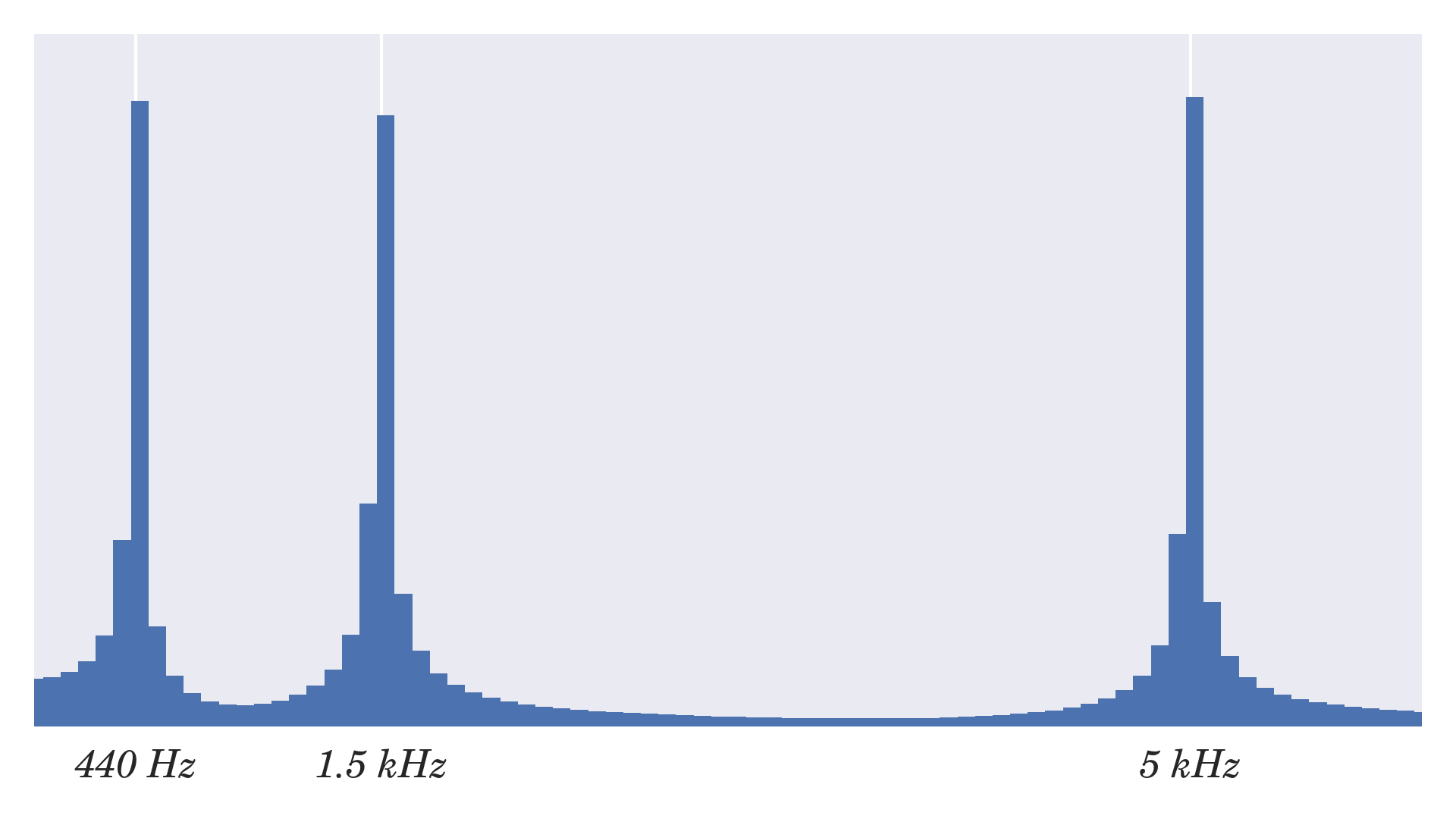
Вот примерный график частоты звуковой волны, состоящий из трех тонов — 440 Гц, 1,5 кГц и 5 кГц — с равными амплитудами:

График частотного спектра

Обратите внимание, что это был чисто академический пример, поскольку вычисление дискретного преобразования Фурье с вложенными итерациями имеет O(n<плюс>2) временная сложность, что делает его непригодным для использования на практике. Для реальных приложений вы хотите использовать алгоритм быстрого преобразования Фурье (БПФ), который лучше всего реализован в библиотеке C, такой как БПФ в SciPy.

Заключение

Простота использования комплексных чисел в Python делает их удивительно интересным и практичным инструментом. Вы увидели двумерные векторы, реализованные практически бесплатно, и благодаря им смогли проанализировать звуковые частоты. Комплексные числа позволяют элегантно выражать математические формулы в коде без использования шаблонного синтаксиса.

В этом руководстве вы узнали, как:

• Определение комплексных чисел с помощью литералов в Python
• Представляют комплексные числа в прямоугольных и полярных координатах
• Используйте комплексные числа в арифметических выражениях
• воспользуйтесь встроенным cmath модуль
• Переводить математические формулы непосредственно в код Python

Каков ваш опыт работы с комплексными числами на Python до сих пор? Они вас когда-нибудь пугали? Как вы думаете, какие еще интересные задачи они позволят вам решить?

Вы можете перейти по ссылке ниже, чтобы получить полный исходный код этого руководства:

Получите пример кода: Нажмите здесь, чтобы получить пример кода, который вы будете использовать для изучения комплексных чисел в Python в этом руководстве.

<статус завершения article-slug="python-complex-numbers" class="btn-group mb-0" data-api-article-bookmark-url="/api/v1/articles/python-complex-numbers/bookmark/" данные-api-статья-статус завершения-url="/api/v1/articles/python-complex-numbers/completion_status/"> <поделиться-кнопка bluesky-text="Интересная статья #Python от @realpython.com :" email-body="Проверить эта статья о Python:%0A%0простим сложные числа с помощью Python" email-subject="Статья о Python для вас" twitter-text="Интересная статья о Python от @realpython:" url="https://realpython.com/python-complex-numbers/" url-title="Упрощение комплексных чисел с помощью Python">

Back to Top