Научный Python: использование SciPy для оптимизации
Оглавление
- Различие между SciPy - экосистемой и SciPy-библиотекой
- Понимание модулей SciPy
- Установка SciPy на Ваш компьютер
- Использование модуля Cluster в SciPy
- Использование модуля оптимизации в SciPy
- Заключение
Если вы хотите выполнить научную работу на Python, первая библиотека, к которой вы можете обратиться, - это SciPy. Как вы увидите в этом руководстве, SciPy - это не просто библиотека, а целая экосистема библиотек, которые работают сообща, помогая вам быстро решать сложные научные задачи и надежно.
В этом руководстве вы узнаете, как:
- Найдите информацию обо всем, что вы можете сделать с помощью SciPy
- Установите SciPy на свой компьютер
- Используйте SciPy для кластеризации набора данных по нескольким переменным
- Используйте SciPy для нахождения оптимума функции
Вы можете ознакомиться с примерами из этого руководства, загрузив исходный код, доступный по ссылке ниже:
Получите пример кода: Нажмите здесь, чтобы получить пример кода, который вы будете использовать для ознакомления с SciPy в этом руководстве.
Чем отличаются SciPy от экосистемы и SciPy от библиотеки
Если вы хотите использовать Python для научных вычислительных задач, вам, вероятно, посоветуют использовать несколько библиотек, в том числе:
- NumPy
- SciPy
- Matplotlib
- IPython
- SymPy
- Pandas
В совокупности эти библиотеки составляют экосистему SciPy и предназначены для совместной работы. Многие из них напрямую используют массивы NumPy для выполнения вычислений. Предполагается, что в этом руководстве вы немного знакомы с созданием массивов NumPy и работой с ними.
Примечание: Если вам нужно быстро освоить NumPy, то вы можете ознакомиться с этими руководствами:
- Смотри, Мама, никаких
forЦиклов: Программирование массивов с помощью NumPy - NumPy
arange(): Как использоватьnp.arange() - MATLAB против Python: Обзор основных операций с массивами
В этом руководстве вы узнаете о библиотеке SciPy, одном из ключевых компонентов
экосистемы SciPy. Библиотека SciPy - это фундаментальная библиотека для научных вычислений на Python. Он предоставляет множество эффективных и удобных интерфейсов для решения таких задач, как численное интегрирование, оптимизация, обработка сигналов, линейная алгебра и многое другое.
Общие сведения о модулях SciPy
Библиотека SciPy состоит из ряда модулей, которые разделяют библиотеку на отдельные функциональные блоки. Если вы хотите узнать о различных модулях, которые включает SciPy, вы можете запустить help() на scipy, как показано ниже:
>>> import scipy
>>> help(scipy)
В результате будет получена некоторая справка по всей библиотеке SciPy, часть которой показана ниже:
Subpackages
-----------
Using any of these subpackages requires an explicit import. For example,
``import scipy.cluster``.
::
cluster --- Vector Quantization / Kmeans
fft --- Discrete Fourier transforms
fftpack --- Legacy discrete Fourier transforms
integrate --- Integration routines
...
Этот блок кода показывает Subpackages часть выходных данных справки, которая представляет собой список всех доступных модулей в SciPy, которые вы можете использовать для вычислений.
Обратите внимание на текст в верхней части раздела, в котором говорится: "Using any of these subpackages requires an explicit import." Если вы хотите использовать функциональность из модуля в SciPy, вам необходимо импортировать модуль, который вы хотите использовать конкретно. Вы увидите несколько примеров этого чуть позже в руководстве, а рекомендации по импорту библиотек из SciPy приведены в документации SciPy.
Как только вы решите, какой модуль вы хотите использовать, вы можете ознакомиться со ссылкой на SciPy API, которая содержит все подробные сведения о каждом модуле в SciPy. Если вы ищете что-то более подробное, то Конспекты лекций SciPy - отличный ресурс для углубленного изучения многих модулей SciPy.
Далее в этом руководстве вы узнаете о cluster и optimize, которые являются двумя модулями библиотеки SciPy. Но сначала вам нужно установить SciPy на свой компьютер.
Установка SciPy на Ваш компьютер
Как и в случае с большинством пакетов Python, существует два основных способа установки SciPy на ваш компьютер:
Здесь вы узнаете, как использовать оба этих подхода для установки библиотеки. Единственной прямой зависимостью SciPy является пакет NumPy. Любой из этих методов установки автоматически установит NumPy в дополнение к SciPy, если это необходимо.
Анаконда
Anaconda является популярным дистрибутивом Python, главным образом потому, что он включает в себя готовые версии наиболее популярных пакетов scientific Python для Windows, macOS и Linux. Если на вашем компьютере еще не установлен Python, то Anaconda - отличный вариант для начала работы. Anaconda поставляется с предустановленным SciPy и его необходимыми зависимостями, поэтому после установки Anaconda вам больше ничего не нужно делать!
Вы можете скачать и установить Anaconda с их страницы загрузки. Убедитесь, что вы скачали самую последнюю версию Python 3. Установив программу установки на свой компьютер, вы можете следовать процедуре установки приложения по умолчанию, в зависимости от вашей платформы.
Примечание: Убедитесь, что вы установили Anaconda в каталог, для изменения которого не требуются права администратора. Это настройка в программе установки по умолчанию.
Если у вас уже установлена Anaconda, но вы хотите установить или обновить SciPy, то вы тоже можете это сделать. Откройте приложение terminal в macOS или Linux или запрос Anaconda в Windows и введите одну из следующих строк кода:
$ conda install scipy
$ conda update scipy
Вам следует использовать первую строку, если вам нужно установить SciPy, или вторую строку, если вы просто хотите обновить SciPy. Чтобы убедиться, что SciPy установлен, запустите Python в своем терминале и попробуйте импортировать SciPy:
>>> import scipy
>>> print(scipy.__file__)
/.../lib/python3.7/site-packages/scipy/__init__.py
В этом коде вы импортировали scipy и напечатали расположение файла, из которого загружается scipy. Приведенный выше пример предназначен для macOS. Возможно, на вашем компьютере будет отображаться другое местоположение. Теперь SciPy установлен на вашем компьютере и готов к использованию. Вы можете перейти к следующему разделу, чтобы начать использовать SciPy!
Менеджер пакетов pip
Если у вас уже установлена версия Python, отличная от Anaconda, или вы не хотите использовать Anaconda, то для установки SciPy вы будете использовать pip. Чтобы узнать больше о том, что такое pip, ознакомьтесь с Использованием pip Python для управления зависимостями ваших проектов и Руководством для начинающих по pip.
Примечание: pip устанавливает пакеты, используя формат, называемый wheels. В формате wheel код компилируется перед отправкой на ваш компьютер. Это почти тот же подход, что и в Anaconda, хотя файлы формата wheel немного отличаются от формата Anaconda, и они не взаимозаменяемы.
Чтобы установить SciPy с помощью pip, откройте приложение терминала и введите следующую строку кода:
$ python -m pip install -U scipy
Код установит SciPy, если он еще не установлен, или обновит SciPy, если он установлен. Чтобы убедиться, что SciPy установлен, запустите Python в своем терминале и попробуйте импортировать SciPy:
>>> import scipy
>>> print(scipy.__file__)
/.../lib/python3.7/site-packages/scipy/__init__.py
В этом коде вы импортировали scipy и напечатали местоположение файла, из которого загружается scipy. В приведенном выше примере для macOS используется pyenv. Возможно, на вашем компьютере будет отображаться другое местоположение. Теперь на вашем компьютере установлен SciPy. Давайте посмотрим, как вы можете использовать SciPy для решения нескольких проблем, с которыми вы можете столкнуться!
Использование модуля Cluster в SciPy
Кластеризация - популярный метод категоризации данных путем объединения их в группы. Библиотека SciPy включает в себя реализацию алгоритма кластеризации k-means, а также несколько алгоритмов иерархической кластеризации. В этом примере вы будете использовать алгоритм k-средних в scipy.cluster.vq, где vq означает векторное квантование.
Сначала вам следует взглянуть на набор данных, который вы будете использовать для этого примера. Набор данных состоит из 4827 реальных и 747 текстовых сообщений со спамом (или SMS). Исходный набор данных можно найти в Репозитории машинного обучения UCI или на веб-странице авторов .
Примечание: Данные были собраны компанией Tiago A. Алмейда и Хосе Мария Гомес Идальго и опубликована в статье под названием “Вклад в изучение фильтрации SMS-спама: новая коллекция и результаты” в Материалах симпозиума ACM по разработке документов 2011 года (DOCENG‘11) размещенный в горах Вид, Калифорния, США в 2011 году.
В наборе данных каждое сообщение имеет одну из двух меток:
-
hamдля получения достоверных сообщений -
spamдля спам-сообщений
К каждому ярлыку прилагается полный текст сообщения. При просмотре данных вы можете заметить, что в спам-сообщениях, как правило, много цифр. В них часто указывается номер телефона или сумма выигрыша. Давайте определим, является ли сообщение спамом, основываясь на количестве цифр в нем. Для этого вам нужно сгруппировать данные в три группы в зависимости от количества цифр, которые появляются в сообщении:
-
Не является спамом: Предполагается, что сообщения с наименьшим количеством цифр не будут считаться спамом.
-
Неизвестно: Сообщения с промежуточным количеством цифр неизвестны и требуют обработки с помощью более продвинутых алгоритмов.
-
Спам: Сообщения с наибольшим количеством цифр считаются спамом.
Давайте начнем с кластеризации текстовых сообщений. Сначала вам следует импортировать библиотеки, которые вы будете использовать в этом примере:
1from pathlib import Path
2import numpy as np
3from scipy.cluster.vq import whiten, kmeans, vq
Вы можете видеть, что импортируете три функции из scipy.cluster.vq. Каждая из этих функций принимает в качестве входных данных массив NumPy. Эти массивы должны содержать объектов набора данных в столбцах и наблюдений в строках.
Объект - это переменная, представляющая интерес, в то время как наблюдение создается каждый раз, когда вы записываете каждый объект. В этом примере в наборе данных содержится 5574 наблюдения, или отдельных сообщения. Кроме того, вы увидите, что есть две функции:
- Количество цифр в текстовом сообщении
- Количество раз, когда это количество цифр появляется во всем наборе данных
Далее вам следует загрузить файл данных из базы данных UCI. Данные поступают в виде текстового файла, где класс сообщения отделен от самого сообщения символом табуляции, а каждое сообщение находится в отдельной строке. Вы должны записать данные в список, используя pathlib.Path:
4data = Path("SMSSpamCollection").read_text()
5data = data.strip()
6data = data.split("\n")
В этом коде вы используете pathlib.Path.read_text() для преобразования файла в строку. Затем вы используете .strip(), чтобы удалить все конечные пробелы и разделить строку на список с .split().
Далее вы можете приступить к анализу данных. Вам нужно подсчитать количество цифр, которые появляются в каждом текстовом сообщении. Python включает collections.Counter в стандартную библиотеку для сбора количества объектов в структуре, подобной словарю. Однако, поскольку все функции в scipy.cluster.vq ожидают, что в качестве входных данных будут использоваться массивы NumPy, вы не можете использовать collections.Counter в этом примере. Вместо этого вы используете массив NumPy и выполняете подсчет вручную.
Опять же, вас интересует количество цифр в данном SMS-сообщении и в скольких SMS-сообщениях содержится такое количество цифр. Во-первых, вы должны создать массив NumPy, который связывает количество цифр в данном сообщении с результатом отправки сообщения, независимо от того, было ли это ветчиной или спамом:
7digit_counts = np.empty((len(data), 2), dtype=int)
В этом коде вы создаете пустой массив NumPy, digit_counts, который содержит два столбца и 5574 строки. Количество строк равно количеству сообщений в наборе данных. Вы будете использовать digit_counts, чтобы связать количество цифр в сообщении со спамом или нет.
Вы должны создать массив перед входом в цикл, чтобы вам не приходилось выделять новую память по мере расширения вашего массива. Это повышает эффективность вашего кода. Далее вы должны обработать данные, чтобы записать количество цифр и статус сообщения:
8for i, line in enumerate(data):
9 case, message = line.split("\t")
10 num_digits = sum(c.isdigit() for c in message)
11 digit_counts[i, 0] = 0 if case == "ham" else 1
12 digit_counts[i, 1] = num_digits
Вот пошаговое описание того, как работает этот код:
-
Строка 8: Повторяем цикл по
data. Вы используетеenumerate(), чтобы поместить значение из списка вlineи создать индексiдля этого списка. Чтобы узнать больше оenumerate(), ознакомьтесь с Pythonenumerate(): Упрощение циклов, для которых требуются счетчики. -
Строка 9: Разделите строку символом табуляции, чтобы создать
caseиmessage.case- это строка, которая указывает, является ли сообщениеhamилиspam, в то время какmessage- это строка с текстом сообщения. -
Строка 10: Вычислите количество цифр в сообщении с помощью
sum()о каком-то понимании. В процессе понимания вы проверяете каждый символ в сообщении, используяisdigit(),, который возвращаетTrue, если элемент является цифрой, иFalseв противном случае.sum()затем обрабатывает каждый результатTrueкак 1, а каждый результатFalseкак 0. Итак, результатомsum()при таком понимании является количество символов, для которых возвращеноisdigit()True. -
Строка 11: Присвойте значения
digit_counts. Вы присваиваете первому столбцу строкиiзначение 0, если сообщение было подлинным (ham), или 1, если сообщение было спамом. -
Строка 12: Присвоить значения
digit_counts. Вы назначаете второму столбцу строкиiколичество цифр в сообщении.
Теперь у вас есть массив NumPy, содержащий количество цифр в каждом сообщении. Однако вы хотите применить алгоритм кластеризации к массиву, который содержит количество сообщений с определенным количеством цифр. Другими словами, вам нужно создать массив, в котором первый столбец содержит количество цифр в сообщении, а второй столбец - количество сообщений, содержащих это количество цифр. Ознакомьтесь с приведенным ниже кодом:
13unique_counts = np.unique(digit_counts[:, 1], return_counts=True)
np.unique() принимает массив в качестве первого аргумента и возвращает другой массив с уникальными элементами из аргумента. Также принимает несколько необязательных аргументов. Здесь вы используете return_counts=True, чтобы указать np.unique() также возвращать массив с указанием количества раз, когда каждый уникальный элемент присутствует во входном массиве. Эти два выходных данных возвращаются в виде кортежа, который вы сохраняете в unique_counts.
Далее вам нужно преобразовать unique_counts в форму, подходящую для кластеризации:
14unique_counts = np.transpose(np.vstack(unique_counts))
Вы объединяете два вывода 1xN из np.unique() в один массив 2xN, используя np.vstack(), а затем преобразуете их в массив Nx2. Этот формат вы будете использовать в функциях кластеризации. Каждая строка в unique_counts теперь содержит два элемента:
- Количество цифр в сообщении
- Количество сообщений, в которых было такое количество цифр
Ниже показано подмножество выходных данных этих двух операций:
[[ 0 4110]
[ 1 486]
[ 2 160]
...
[ 40 4]
[ 41 2]
[ 47 1]]
В наборе данных имеется 4110 сообщений, в которых нет цифр, 486 сообщений содержат 1 цифру и так далее. Теперь вам следует применить алгоритм кластеризации с использованием k-средних к этому массиву:
15whitened_counts = whiten(unique_counts)
16codebook, _ = kmeans(whitened_counts, 3)
Вы используете whiten() для нормализации каждого признака, чтобы получить единичную дисперсию, что улучшает результаты по сравнению с kmeans(). Затем kmeans() принимает в качестве аргументов выделенные данные и количество создаваемых кластеров. В этом примере вы хотите создать 3 кластера, например, для определенно хам, определенно спам и неизвестно. kmeans() возвращает два значения:
-
Массив с тремя строками и двумя столбцами, представляющими центроиды каждой группы: Алгоритм
kmeans()вычисляет оптимальное местоположение центроида каждого кластера путем минимизации расстояния от наблюдений до каждого центроида. Этот массив присваиваетсяcodebook. -
Среднее евклидово расстояние от наблюдений до центроидов: Для остальной части этого примера это значение не понадобится, поэтому вы можете присвоить ему значение
_.
Далее вы должны определить, к какому кластеру относится каждое наблюдение, используя vq():
17codes, _ = vq(whitened_counts, codebook)
vq() присваивает коды из codebook каждому наблюдению. Возвращает два значения:
-
Первое значение представляет собой массив той же длины, что и
unique_counts, где значение каждого элемента представляет собой целое число, представляющее, к какому кластеру относится данное наблюдение. Поскольку в этом примере вы использовали три кластера, каждое наблюдение присваивается кластеру0,1, или2. -
Второе значение представляет собой массив евклидовых расстояний между каждым наблюдением и его центром тяжести.
Теперь, когда у вас есть сгруппированные данные, вы должны использовать их для составления прогнозов относительно SMS-сообщений. Вы можете проверить количество цифр, чтобы определить, на каком уровне алгоритм кластеризации провел границу между определенно нежелательной почтой и неизвестной, а также между неизвестной и определенно нежелательной почтой.
Алгоритм кластеризации случайным образом присваивает код 0, 1, или 2 каждому кластеру, поэтому вам нужно определить, какой из них какой. Вы можете использовать этот код, чтобы найти код, связанный с каждым кластером:
18ham_code = codes[0]
19spam_code = codes[-1]
20unknown_code = list(set(range(3)) ^ set((ham_code, spam_code)))[0]
В этом коде в первой строке содержится код, связанный с сообщениями ham. Согласно нашей гипотезе, приведенной выше, сообщения ham содержат наименьшее количество цифр, и массив цифр был отсортирован от наименьшего к наибольшему количеству цифр. Таким образом, кластер сообщений ham запускается в начале codes.
Аналогично, спам-сообщения содержат наибольшее количество цифр и образуют последний кластер в codes. Таким образом, код для спам-сообщений будет равен последнему элементу codes. Наконец, вам нужно найти код для неизвестных сообщений. Поскольку существует только 3 варианта кода, и вы уже определили два из них, вы можете использовать оператор symmetric_difference в Python set для определения последнего значения кода. Затем вы можете распечатать кластер, связанный с каждым типом сообщения:
21print("definitely ham:", unique_counts[codes == ham_code][-1])
22print("definitely spam:", unique_counts[codes == spam_code][-1])
23print("unknown:", unique_counts[codes == unknown_code][-1])
В этом коде каждая строка получает строки в unique_counts, где vq() присвоены разные значения кодов. Поскольку эта операция возвращает массив, вы должны получить последнюю строку массива, чтобы определить наибольшее количество цифр, присвоенных каждому кластеру. Результат показан ниже:
definitely ham: [0 4110]
definitely spam: [47 1]
unknown: [20 18]
В этом выводе вы видите, что сообщения определенно бесполезны - это сообщения с нулевыми цифрами в сообщении, сообщения неизвестны - это сообщения с нулевыми цифрами в сообщении. все, что содержит от 1 до 20 цифр, и определенно является спамом. сообщения содержат все, что содержит от 21 до 47 цифр, что является максимальным количеством цифр в вашем наборе данных.
Теперь вам следует проверить, насколько точны ваши прогнозы на основе этого набора данных. Сначала создайте несколько масок для digit_counts, чтобы вы могли легко получить статус ham или spam сообщений:
24digits = digit_counts[:, 1]
25predicted_hams = digits == 0
26predicted_spams = digits > 20
27predicted_unknowns = np.logical_and(digits > 0, digits <= 20)
В этом коде вы создаете маску predicted_hams, в которой в сообщении нет цифр. Затем вы создаете маску predicted_spams для всех сообщений, содержащих более 20 цифр. Наконец, сообщения в середине следующие: predicted_unknowns.
Затем примените эти маски к фактическому количеству цифр, чтобы получить предсказания:
28spam_cluster = digit_counts[predicted_spams]
29ham_cluster = digit_counts[predicted_hams]
30unk_cluster = digit_counts[predicted_unknowns]
Здесь вы применяете маски, созданные в последнем блоке кода, к массиву digit_counts. Это создает три новых массива, содержащих только те сообщения, которые были сгруппированы в каждую группу. Наконец, вы можете увидеть, сколько сообщений каждого типа попало в каждый кластер:
31print("hams:", np.unique(ham_cluster[:, 0], return_counts=True))
32print("spams:", np.unique(spam_cluster[:, 0], return_counts=True))
33print("unknowns:", np.unique(unk_cluster[:, 0], return_counts=True))
Этот код выводит количество каждого уникального значения из кластеров. Помните, что 0 означает, что сообщение было ham, а 1 означает, что сообщение было spam. Результаты приведены ниже:
hams: (array([0, 1]), array([4071, 39]))
spams: (array([0, 1]), array([ 1, 232]))
unknowns: (array([0, 1]), array([755, 476]))
Из этого вывода вы можете видеть, что 4110 сообщений попали в группу определенно ham, из которых 4071 на самом деле были ham и только 39 были спамом. И наоборот, из 233 сообщений, попавших в группу определенно спам, только 1 было на самом деле спамом, а остальные - спамом.
Конечно, более 1200 сообщений попали в категорию неизвестных, поэтому для классификации этих сообщений потребуется более углубленный анализ. Возможно, вам захочется изучить что-то вроде обработки на естественном языке, чтобы повысить точность ваших прогнозов, и вы можете использовать Python и Keras, чтобы помочь в этом.
Использование модуля оптимизации в SciPy
Когда вам нужно оптимизировать входные параметры функции, scipy.optimize содержит ряд полезных методов для оптимизации различных типов функций:
minimize_scalar()иminimize()для минимизации функции одной переменной и функции многих переменных, соответственноcurve_fit()чтобы сопоставить функцию с набором данныхroot_scalar()иroot()для нахождения нулей функции одной переменной и многих переменных соответственноlinprog()чтобы минимизировать линейную целевую функцию с линейным неравенством и ограничениями на равенство
На практике все эти функции выполняют ту или иную оптимизацию . В этом разделе вы узнаете о двух функциях минимизации: minimize_scalar() и minimize().
Минимизация функции с помощью одной переменной
Математическая функция, которая принимает одно число и выдает один результат, называется скалярной функцией. Обычно это противопоставляется многомерным функциям, которые принимают несколько чисел и также выдают несколько выходных данных. В следующем разделе вы увидите пример оптимизации многомерных функций.
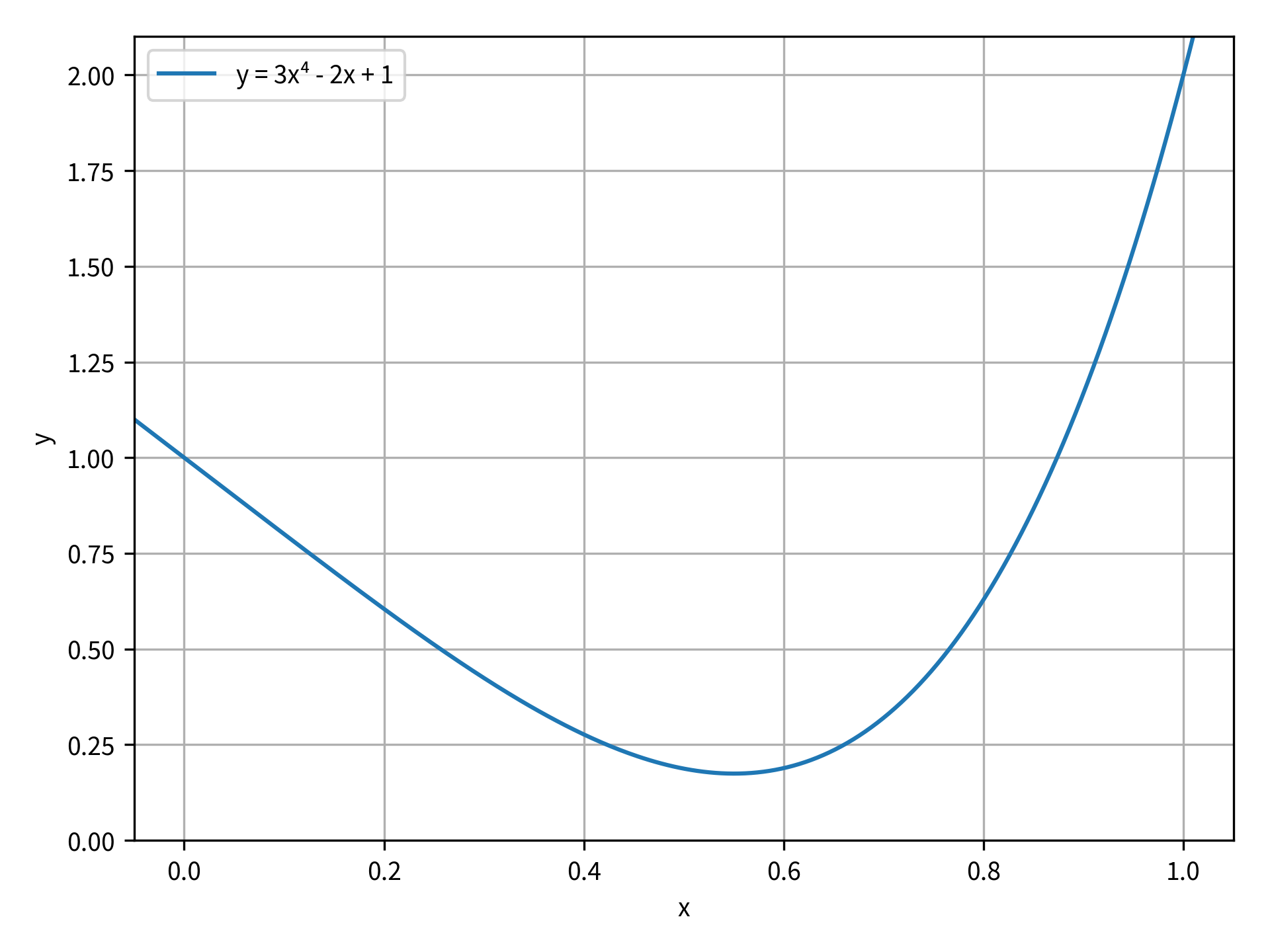
В этом разделе ваша скалярная функция будет представлять собой квартичный многочлен, и ваша цель - найти минимальное значение этой функции. Функция имеет вид y = 3x⁴ - 2x + 1. На рисунке ниже приведен график функции для диапазона значений x от 0 до 1:
На рисунке вы можете видеть, что минимальное значение этой функции составляет приблизительно x = 0,55. Вы можете использовать minimize_scalar() для определения точных координат x и y минимума. Сначала импортируйте minimize_scalar() из scipy.optimize. Затем вам нужно определить целевую функцию, которая должна быть сведена к минимуму:
1from scipy.optimize import minimize_scalar
2
3def objective_function(x):
4 return 3 * x ** 4 - 2 * x + 1
objective_function() принимает входные данные x и применяет к ним необходимые математические операции, затем возвращает результат. В определении функции вы можете использовать любые математические функции, которые вам нужны. Единственное ограничение заключается в том, что функция должна возвращать одно число в конце.
Затем используйте minimize_scalar(), чтобы найти минимальное значение этой функции. minimize_scalar() имеет только один обязательный ввод, который является именем определения целевой функции:
5res = minimize_scalar(objective_function)
Выходные данные minimize_scalar() являются экземпляром OptimizeResult. Этот класс собирает воедино многие важные сведения о работе оптимизатора, в том числе о том, была ли оптимизация успешной и, в случае успеха, каков был конечный результат. Выходные данные minimize_scalar() для этой функции показаны ниже:
fun: 0.17451818777634331
nfev: 16
nit: 12
success: True
x: 0.5503212087491959
Все эти результаты являются атрибутами OptimizeResult. success это Логическое значение, указывающее, успешно ли завершена оптимизация. Если оптимизация прошла успешно, то fun - это значение целевой функции при оптимальном значении x. Из выходных данных видно, что, как и ожидалось, оптимальное значение для этой функции было близко к x = 0.55.
Примечание: Как вы, наверное, знаете, не у каждой функции есть минимум. Например, попробуйте посмотреть, что произойдет, если ваша целевая функция равна y = x3. Для minimize_scalar() целевые функции без минимума часто приводят к OverflowError, потому что оптимизатор в конечном итоге пытается получить число, которое слишком велико для вычисления компьютером.
На противоположной стороне от функций без минимума находятся функции, которые имеют несколько минимумов. В этих случаях minimize_scalar() не гарантирует нахождения глобального минимума функции. Однако minimize_scalar() имеет аргумент ключевого слова method, который вы можете указать для управления решателем, используемым для оптимизации. Библиотека SciPy имеет три встроенных метода скалярной минимизации:
brentявляется реализацией алгоритма Брента. Этот метод используется по умолчанию.goldenявляется реализацией поиска по золотому сечению. В документации отмечается, что метод Брента обычно лучше.boundedэто ограниченная реализация алгоритма Брента. Полезно ограничить область поиска, когда минимум находится в известном диапазоне.
, когда method равно либо brent, либо golden, minimize_scalar() принимает другой аргумент с именем bracket. Это последовательность из двух или трех элементов, которые дают первоначальное представление о границах области с минимумом. Однако эти методы решения не гарантируют, что найденный минимум будет находиться в пределах этого диапазона.
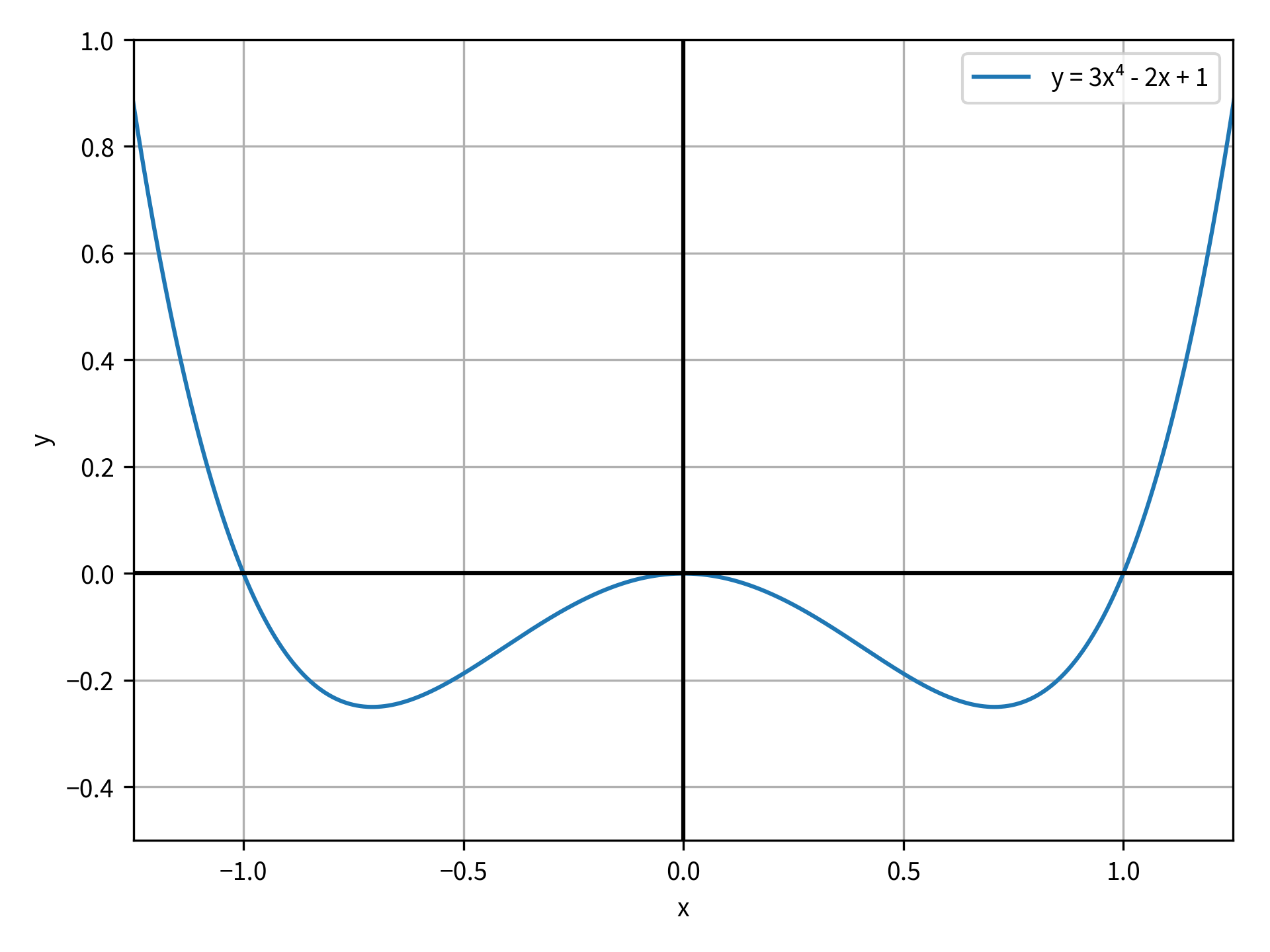
С другой стороны, когда method равно bounded, minimize_scalar() принимает другой аргумент, называемый bounds. Это последовательность из двух элементов, которая строго ограничивает область поиска минимума. Попробуйте использовать метод bounded с функцией y = x⁴ - x2. Эта функция представлена на рисунке ниже:
Используя предыдущий пример кода, вы можете переопределить objective_function() следующим образом:
7def objective_function(x):
8 return x ** 4 - x ** 2
Сначала попробуйте метод по умолчанию brent:
9res = minimize_scalar(objective_function)
В этом коде вы не передавали значение для method, поэтому minimize_scalar() по умолчанию использовал метод brent. Результат таков:
fun: -0.24999999999999994
nfev: 15
nit: 11
success: True
x: 0.7071067853059209
Вы можете видеть, что оптимизация прошла успешно. Было найдено оптимальное значение при x = 0,707 и y = -1/4. Если вы решите для минимума уравнения аналитически, то вы найдете минимум при x = 1/√ 2, что очень близко к ответу, найденному с помощью функции минимизации. Однако, что, если бы вы захотели найти симметричный минимум при x = -1/√2? Вы можете вернуть тот же результат, указав аргумент bracket методу brent:
10res = minimize_scalar(objective_function, bracket=(-1, 0))
В этом коде вы вводите последовательность от (-1, 0) до bracket, чтобы начать поиск в диапазоне от -1 до 0. Вы ожидаете, что в этой области будет минимум, поскольку целевая функция симметрична относительно оси y. Однако даже при использовании bracket метод brent по-прежнему возвращает минимальное значение при x = +1/√2. Чтобы найти минимум при x = -1/√2, вы можете использовать метод bounded с bounds:
11res = minimize_scalar(objective_function, method='bounded', bounds=(-1, 0))
В этом коде вы добавляете method и bounds в качестве аргументов к minimize_scalar(), а для bounds задаете значение от -1 до 0. Результат этого метода выглядит следующим образом:
fun: -0.24999999999998732
message: 'Solution found.'
nfev: 10
status: 0
success: True
x: -0.707106701474177
Как и ожидалось, минимум был найден при x = -1/√2. Обратите внимание на дополнительный результат этого метода, который включает атрибут message в res. Это поле часто используется для получения более подробных выходных данных некоторыми решателями задач минимизации.
Минимизация функции со многими переменными
scipy.optimize также включает в себя более общие minimize(). Эта функция может обрабатывать многомерных входов и выходов и имеет более сложные алгоритмы оптимизации, чтобы справиться с этим. Кроме того, minimize() может обрабатывать ограничений для решения вашей задачи. Вы можете указать три типа ограничений:
LinearConstraint: Решение ограничено путем вычисления внутреннего произведения значений решения x с помощью пользовательского массива-input и сравнения результата с нижней и верхней границами.NonlinearConstraint: Решение ограничено путем применения пользовательской функции к значениям решения x и сравнения возвращаемого значения с нижней и верхней границами.Bounds: Значения решения x должны находиться между нижней и верхней границами.
Когда вы используете эти ограничения, это может ограничить выбор конкретного метода оптимизации, который вы можете использовать, поскольку не все доступные методы поддерживают ограничения таким образом.
Давайте попробуем продемонстрировать, как использовать minimize(). Представьте, что вы биржевой брокер, который заинтересован в максимизации общего дохода от продажи определенного количества ваших акций. Вы определили определенный круг покупателей, и для каждого покупателя вы знаете цену, которую он заплатит, и сколько наличных денег у него есть на руках.
Вы можете сформулировать эту проблему как задачу ограниченной оптимизации. Целевая функция заключается в том, что вы хотите максимизировать свой доход. Однако minimize() определяет минимальное значение функции, поэтому вам нужно умножить вашу целевую функцию на -1, чтобы найти значения x, которые дают наибольшее отрицательное число.
В этой проблеме есть одно ограничение, которое заключается в том, что сумма всех акций, приобретенных покупателями, не превышает количества акций, имеющихся у вас в наличии. Также существуют ограничения для каждой из переменных решения, поскольку у каждого покупателя есть верхняя граница наличности, а нижняя граница равна нулю. Отрицательные значения x для решения означают, что вы будете платить покупателям!
Попробуйте использовать приведенный ниже код для решения этой проблемы. Сначала импортируйте необходимые модули, а затем задайте переменные для определения количества покупателей на рынке и количества акций, которые вы хотите продать:
1import numpy as np
2from scipy.optimize import minimize, LinearConstraint
3
4n_buyers = 10
5n_shares = 15
В этом коде вы импортируете numpy, minimize(), и LinearConstraint из scipy.optimize. Затем вы устанавливаете рынок из 10 покупателей, которые в общей сложности купят у вас 15 акций.
Затем создайте массивы для хранения цены, которую платит каждый покупатель, максимальной суммы, которую он может позволить себе потратить, и максимального количества акций, которые каждый покупатель может себе позволить, учитывая первые два массива. В этом примере вы можете использовать генерацию случайных чисел в np.random для генерации массивов:
6np.random.seed(10)
7prices = np.random.random(n_buyers)
8money_available = np.random.randint(1, 4, n_buyers)
В этом коде вы задаете начальное значение для генераторов случайных чисел NumPy. Эта функция гарантирует, что при каждом запуске этого кода вы будете получать один и тот же набор случайных чисел. Это сделано для того, чтобы убедиться, что ваши выходные данные совпадают с данными руководства для сравнения.
В строке 7 вы генерируете массив цен, которые будут платить покупатели. np.random.random() создает массив случайных чисел на полуоткрытом интервале [0, 1). Количество элементов в массиве определяется значением аргумента, которым в данном случае является количество покупателей.
В строке 8 вы генерируете массив целых чисел на полуоткрытом интервале из [1, 4), опять же с указанием количества покупателей. Этот массив представляет общую сумму наличных денег, доступную каждому покупателю. Теперь вам нужно вычислить максимальное количество акций, которое может приобрести каждый покупатель:
9n_shares_per_buyer = money_available / prices
10print(prices, money_available, n_shares_per_buyer, sep="\n")
В строке 9 вы берете соотношение money_available и prices, чтобы определить максимальное количество акций, которое может приобрести каждый покупатель. Наконец, вы выводите каждый из этих массивов, разделенных новой строкой. Результат показан ниже:
[0.77132064 0.02075195 0.63364823 0.74880388 0.49850701 0.22479665
0.19806286 0.76053071 0.16911084 0.08833981]
[1 1 1 3 1 3 3 2 1 1]
[ 1.29647768 48.18824404 1.57816269 4.00638948 2.00598984 13.34539487
15.14670609 2.62974258 5.91328161 11.3199242 ]
Первая строка представляет собой массив цен, которые представляют собой числа с плавающей запятой в диапазоне от 0 до 1. За этой строкой следует максимальное количество доступных денежных средств в целых числах от 1 до 4. Наконец, вы увидите количество акций, которые может приобрести каждый покупатель.
Теперь вам нужно создать ограничения и границы для решателя. Ограничение заключается в том, что сумма всех приобретенных акций не может превышать общее количество доступных акций. Это скорее ограничение, чем привязка, поскольку оно включает в себя более одной переменной решения.
Чтобы представить это математически, вы могли бы сказать, что x[0] + x[1] + ... + x[n] = n_shares, где n - общее количество покупателей. Более кратко, вы могли бы взять точку или внутреннее произведение вектора единиц на значения решения и ограничить его равным n_shares. Помните, что LinearConstraint принимает скалярное произведение входного массива на значения решения и сравнивает его с нижней и верхней границами. Вы можете использовать это для настройки ограничения на n_shares:
11constraint = LinearConstraint(np.ones(n_buyers), lb=n_shares, ub=n_shares)
В этом коде вы создаете массив единиц длиной n_buyers и передаете его в качестве первого аргумента в LinearConstraint. Поскольку LinearConstraint принимает скалярное произведение вектора решения с этим аргументом, результатом будет сумма приобретенных акций.
Этот результат затем должен находиться между двумя другими аргументами:
- Нижняя граница
lb - Верхняя граница
ub
Поскольку lb = ub = n_shares, это ограничение на равенство, поскольку сумма значений должна быть равна как lb, так и ub. Если бы lb отличалось от ub, то это было бы ограничение неравенства.
Затем создайте границы для переменной solution. Эти границы ограничивают количество приобретаемых акций равным 0 в нижней части и n_shares_per_buyer в верхней части. Формат, который minimize() ожидает для границ, представляет собой последовательность кортежей нижних и верхних границ:
12bounds = [(0, n) for n in n_shares_per_buyer]
В этом коде вы используете понимание для создания списка кортежей для каждого покупателя. Последним шагом перед запуском оптимизации является определение целевой функции. Помните, что вы пытаетесь максимизировать свой доход. Аналогично, вы хотите, чтобы отрицательная величина вашего дохода была как можно большим отрицательным числом.
Доход, который вы получаете от каждой продажи, - это цена, которую платит покупатель, умноженная на количество акций, которые он покупает. Математически это можно записать как prices[0]*x[0] + prices[1]*x[1] + ... + prices[n]*x[n], где n - это снова общее количество покупателей.
Еще раз, вы можете представить это более кратко с помощью внутреннего продукта или x.dot(prices). Это означает, что ваша целевая функция должна принимать текущие значения решения x и массив цен в качестве аргументов:
13def objective_function(x, prices):
14 return -x.dot(prices)
В этом коде вы определяете objective_function() как принимающий два аргумента. Затем вы берете скалярное произведение x на prices и возвращаете отрицательное значение этого значения. Помните, что вы должны вернуть отрицательное значение, потому что вы пытаетесь сделать это число как можно меньше или как можно ближе к отрицательной бесконечности. Наконец, вы можете вызвать minimize():
15res = minimize(
16 objective_function,
17 x0=10 * np.random.random(n_buyers),
18 args=(prices,),
19 constraints=constraint,
20 bounds=bounds,
21)
В этом коде res является экземпляром OptimizeResult, как и в случае с minimize_scalar(). Как вы увидите, здесь много одинаковых полей, хотя проблема совсем в другом. При вызове minimize() вы передаете пять аргументов:
-
objective_function: Первым позиционным аргументом должна быть функция, которую вы оптимизируете. -
x0: Следующий аргумент - это начальное предположение о значениях решения. В этом случае вы просто предоставляете случайный массив значений от 0 до 10 длинойn_buyers. Для некоторых алгоритмов или задач может быть важно выбрать подходящее начальное предположение. Однако для данного примера это не кажется слишком важным. -
args: Следующий аргумент - это набор других аргументов, которые необходимо передать в целевую функцию.minimize()всегда будет передаваться текущее значение решенияxвводится в целевую функцию, поэтому этот аргумент служит местом для сбора любых других необходимых входных данных. В этом примере вам нужно передатьpricesвobjective_function(), так что здесь все понятно. -
constraints: Следующий аргумент - это последовательность ограничений на проблему. Вы передаете созданное ранее ограничение на количество доступных общих ресурсов. -
bounds: Последний аргумент - это последовательность оценок переменных решения, которые вы сгенерировали ранее.
Как только решатель запустится, вы должны проверить res, распечатав его:
fun: -8.783020157087478
jac: array([-0.7713207 , -0.02075195, -0.63364828, -0.74880385,
-0.49850702, -0.22479665, -0.1980629 , -0.76053071, -0.16911089,
-0.08833981])
message: 'Optimization terminated successfully.'
nfev: 204
nit: 17
njev: 17
status: 0
success: True
x: array([1.29647768e+00, 2.78286565e-13, 1.57816269e+00,
4.00638948e+00, 2.00598984e+00, 3.48323773e+00, 3.19744231e-14,
2.62974258e+00, 2.38121197e-14, 8.84962214e-14])
В этом выводе вы можете увидеть message и status, указывающие на конечное состояние оптимизации. Для этого оптимизатора статус 0 означает успешное завершение оптимизации, что вы также можете увидеть в message. Поскольку оптимизация прошла успешно, fun показывает значение целевой функции при оптимальных значениях решения. Вы получите доход в размере 8,78 долларов США от этой продажи.
Вы можете увидеть значения x, которые оптимизируют функцию в res.x. В этом случае получается, что вы должны продать примерно 1,3 акции первому покупателю, ноль - второму, 1,6 - третьему, 4,0 - четвертому и так далее.
Вам также следует проверить и убедиться, что установленные вами ограничения соблюдены. Вы можете сделать это с помощью следующего кода:
22print("The total number of shares is:", sum(res.x))
23print("Leftover money for each buyer:", money_available - res.x * prices)
В этом коде вы выводите сумму акций, приобретенных каждым покупателем, которая должна быть равна n_shares. Затем вы выводите разницу между наличностью каждого покупателя в кассе и суммой, которую он потратил. Каждое из этих значений должно быть положительным. Результат этих проверок показан ниже:
The total number of shares is: 15.000000000000002
Leftover money for each buyer: [3.08642001e-14 1.00000000e+00
3.09752224e-14 6.48370246e-14 3.28626015e-14 2.21697984e+00
3.00000000e+00 6.46149800e-14 1.00000000e+00 1.00000000e+00]
Как вы можете видеть, все ограничения на решение были выполнены. Теперь вам следует попробовать изменить задачу таким образом, чтобы решатель не мог найти решение. Измените n_shares на значение 1000, чтобы вы пытались продать 1000 акций этим же покупателям. Когда вы запустите minimize(), вы увидите, что результат будет таким, как показано ниже:
fun: nan
jac: array([nan, nan, nan, nan, nan, nan, nan, nan, nan, nan])
message: 'Iteration limit exceeded'
nfev: 2182
nit: 101
njev: 100
status: 9
success: False
x: array([nan, nan, nan, nan, nan, nan, nan, nan, nan, nan])
Обратите внимание, что атрибут status теперь имеет значение 9, а атрибут message указывает на превышение предела итерации. Невозможно продать 1000 акций, учитывая количество денег, имеющихся у каждого покупателя, и количество покупателей на рынке. Однако вместо того, чтобы выдавать ошибку, minimize() по-прежнему возвращает экземпляр OptimizeResult. Вам необходимо обязательно проверить код состояния, прежде чем приступать к дальнейшим расчетам.
Заключение
В этом руководстве вы узнали об экосистеме SciPy и о том, чем она отличается от библиотеки SciPy. Вы прочитали о некоторых модулях, доступных в SciPy, и узнали, как установить SciPy с помощью Anaconda или pip. Затем вы сосредоточились на некоторых примерах, в которых используются функции кластеризации и оптимизации в SciPy.
В примере кластеризация вы разработали алгоритм для сортировки спам-сообщений от законных сообщений. Используя kmeans(), вы обнаружили, что сообщения, содержащие более 20 цифр, с высокой вероятностью являются спамом!
В примере оптимизация сначала вы нашли минимальное значение математически понятной функции только с одной переменной. Затем вы решили более сложную задачу максимизации прибыли от продажи акций. Используя minimize(), вы нашли оптимальное количество акций для продажи группе покупателей и получили прибыль в размере $8.79!
SciPy - это огромная библиотека, в которой есть еще много модулей для изучения. С теми знаниями, которые у вас есть сейчас, вы хорошо подготовлены для начала изучения!
Вы можете ознакомиться с примерами из этого руководства, загрузив исходный код, доступный по ссылке ниже:
Получите пример кода: Нажмите здесь, чтобы получить пример кода, который вы будете использовать для ознакомления с SciPy в этом руководстве.
Back to Top