Рекурсия в Python: Введение

Оглавление

• Что такое рекурсия?
• Зачем использовать рекурсию?
• Рекурсия в Python
• Начало работы: Обратный отсчет до нуля
• Вычислить факториал
  • Определите факториальную функцию Python
  • Сравнение скоростей реализации факториалов
• Перемещение по вложенному списку
  • Рекурсивный переход по вложенному списку
  • Нерекурсивный переход по вложенному списку
• Обнаружение палиндромов
• Сортировка с помощью функции Быстрой сортировки
  • Выбор сводного элемента
  • Реализация секционирования
  • Использование реализации быстрой сортировки
• Заключение

Смотрите сейчас, к этому уроку прилагается соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным руководством, чтобы углубить свое понимание: Рекурсия в Python

Если вы знакомы с функциями в Python, то вы знаете, что довольно часто одна функция вызывает другую. В Python функция также может вызывать саму себя! Функция, которая вызывает саму себя, называется рекурсивной, а метод использования рекурсивной функции называется рекурсией.

Может показаться странным, что функция вызывает сама себя, но многие типы проблем программирования лучше всего решать рекурсивно. Когда вы сталкиваетесь с такой проблемой, рекурсия - незаменимый инструмент, который должен быть в вашем арсенале.

К концу этого урока вы поймете:

• Что значит для функции вызывать саму себя рекурсивно
• Как дизайн функций Python поддерживает рекурсию
• Какие факторы следует учитывать при выборе того, следует ли решать задачу рекурсивно
• Как реализовать рекурсивную функцию в Python

Затем вы изучите несколько задач программирования на Python, в которых используется рекурсия, и сравните рекурсивное решение с аналогичным нерекурсивным.

Бесплатный бонус: Ознакомьтесь с примером главы из книги "Основы Python: практическое введение в Python 3", чтобы увидеть, как вы можете перейти от начального уровня перейти на промежуточный уровень в Python с полным учебным планом, обновленным до версии Python 3.9.

Что такое рекурсия?

Слово рекурсия происходит от латинского слова recurrere, что означает бежать или спешить назад, возвращаться, откатываться или повторяться. Вот несколько онлайн-определений рекурсии:

• Dictionary.com: Действие или процесс возвращения или бегства назад
• Викисловарь: Процесс определения объекта (обычно функции) в терминах самого этого объекта
• Бесплатный словарь: Метод определения последовательности объектов, таких как выражение, функция или набор, где задано некоторое количество исходных объектов и каждый последующий объект определяется в терминах предыдущих объектов

Рекурсивное определение - это определение, в котором определяемый термин фигурирует в самом определении. Ситуации, связанные с самореференцией, часто возникают в реальной жизни, даже если они не сразу распознаются как таковые. Например, предположим, что вы хотите описать группу людей, которые являются вашими предками. Вы могли бы описать их следующим образом:

Обратите внимание, как определяемое понятие, предки, отображается в своем собственном определении. Это рекурсивное определение.

В программировании рекурсия имеет очень точное значение. Это относится к методу кодирования, при котором функция вызывает саму себя.

Зачем использовать рекурсию?

Большинство задач программирования решаемы без рекурсии. Так что, строго говоря, в рекурсии обычно нет необходимости.

Тем не менее, некоторые ситуации особенно подходят для определения, основанного на самореференции - например, определение предков, показанное выше. Если бы вы разрабатывали алгоритм для обработки такого случая программно, рекурсивное решение, вероятно, было бы более чистым и лаконичным.

Обход древовидных структур данных является еще одним хорошим примером. Поскольку это вложенные структуры, они легко поддаются рекурсивному определению. Нерекурсивный алгоритм для обхода вложенной структуры, вероятно, будет несколько громоздким, в то время как рекурсивное решение будет относительно элегантным. Пример этого приведен ниже в этом руководстве.

С другой стороны, рекурсия подходит не для каждой ситуации. Вот еще несколько факторов, которые следует учитывать:

• Для некоторых задач рекурсивное решение, хотя и возможно, будет скорее неудобным, чем элегантным.
• Рекурсивные реализации часто потребляют больше памяти, чем нерекурсивные.
• В некоторых случаях использование рекурсии может привести к замедлению времени выполнения.

Как правило, читаемость кода является самым важным определяющим фактором. Но это зависит от обстоятельств. Приведенные ниже примеры должны помочь вам понять, когда следует выбирать рекурсию.

Рекурсия в Python

Когда вы вызываете функцию в Python, интерпретатор создает новое локальное пространство имен, чтобы имена, определенные в этой функции, не сталкивались с идентичными именами, определенными в другом месте. Одна функция может вызывать другую, и даже если они обе определяют объекты с одинаковыми именами, все работает нормально, потому что эти объекты существуют в разных пространствах имен .

То же самое справедливо, если несколько экземпляров одной и той же функции выполняются одновременно. Например, рассмотрим следующее определение:

def function():
    x = 10
    function()

Когда function() выполняется в первый раз, Python создает пространство имен и присваивает x значение 10 в этом пространстве имен. Затем function() вызывает сам себя рекурсивно. При втором запуске function() интерпретатор создает второе пространство имен и присваивает 10 также x. Эти два экземпляра имени x отличаются друг от друга и могут сосуществовать, не конфликтуя, поскольку они находятся в разных пространствах имен.

К сожалению, запуск function() в его нынешнем виде приводит к менее чем вдохновляющему результату, как показывает следующая обратная трассировка:

>>> function()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 3, in function
  File "<stdin>", line 3, in function
  File "<stdin>", line 3, in function
  [Previous line repeated 996 more times]
RecursionError: maximum recursion depth exceeded

Как написано, function() теоретически будет продолжаться вечно, вызывая себя снова и снова, и ни один из вызовов никогда не будет повторен. На практике, конечно, ничто по-настоящему не вечно. На вашем компьютере не так много памяти, и рано или поздно она закончится.

Python не допускает этого. Интерпретатор ограничивает максимальное количество раз, когда функция может вызывать саму себя рекурсивно, и когда он достигает этого предела, он генерирует RecursionError исключение, как вы видите выше.

Техническое примечание: Вы можете узнать, каков предел рекурсии в Python, с помощью функции из модуля sys, которая называется getrecursionlimit():

>>> from sys import getrecursionlimit
>>> getrecursionlimit()
1000

Вы также можете изменить его с помощью setrecursionlimit():

>>> from sys import setrecursionlimit
>>> setrecursionlimit(2000)
>>> getrecursionlimit()
2000

Вы можете сделать его довольно большим, но вы не можете сделать его бесконечным.

Нет особого смысла в том, чтобы функция без разбора вызывала сама себя рекурсивно без конца. Это напоминает инструкции, которые вы иногда находите на бутылочках с шампунем: “Вспенить, смыть, повторить”. Если бы вы следовали этим инструкциям буквально, вы бы всегда мыли волосы шампунем!

Очевидно, что некоторые производители шампуней допустили этот логический изъян, потому что на некоторых бутылочках с шампунем вместо этого написано “Вспенить, смыть, повторить по мере необходимости ”. Это является условием завершения использования в инструкции. Предположительно, в конце концов вы почувствуете, что ваши волосы достаточно чистые, чтобы не прибегать к дополнительным процедурам. После этого мытье головы можно прекратить.

Аналогично, функция, вызывающая саму себя рекурсивно, должна иметь план, позволяющий в конечном итоге остановиться. Рекурсивные функции обычно выполняются по следующей схеме:

• Существует один или несколько базовых вариантов, которые разрешимы напрямую без необходимости дальнейшей рекурсии.
• Каждый рекурсивный вызов постепенно приближает решение к базовому варианту.

Теперь вы готовы увидеть, как это работает, на нескольких примерах.

Начало работы: Обратный отсчет до нуля

Первым примером является функция с именем countdown(), которая принимает положительное число в качестве аргумента и выводит числа из указанного аргумента вплоть до нуля:

>>> def countdown(n):
...     print(n)
...     if n == 0:
...         return             # Terminate recursion
...     else:
...         countdown(n - 1)   # Recursive call
...

>>> countdown(5)
5
4
3
2
1
0

Обратите внимание, как countdown() соответствует парадигме рекурсивного алгоритма, описанного выше:

• Базовый вариант имеет место, когда n равно нулю, и в этот момент рекурсия прекращается.
• В рекурсивном вызове аргумент на единицу меньше текущего значения n, поэтому каждая рекурсия приближается к базовому варианту.

Примечание: Для простоты countdown() не проверяет свой аргумент на достоверность. Если n является либо нецелым числом, либо отрицательным, вы получите исключение RecursionError, поскольку базовый вариант никогда не достигается.

Версия countdown(), показанная выше, четко описывает базовый вариант и рекурсивный вызов, но есть более краткий способ выразить это:

def countdown(n):
    print(n)
    if n > 0:
        countdown(n - 1)

Вот одна из возможных нерекурсивных реализаций для сравнения:

>>> def countdown(n):
...     while n >= 0:
...         print(n)
...         n -= 1
...

>>> countdown(5)
5
4
3
2
1
0

Это тот случай, когда нерекурсивное решение, по крайней мере, столь же ясно и интуитивно, как и рекурсивное, а возможно, и более того.

Вычислить факториал

В следующем примере используется математическая концепция факториала. Факториал целого положительного числа n, обозначаемый как n!, определяется следующим образом:

Другими словами, n! - это произведение всех целых чисел от 1 до n включительно.

Факториал настолько хорошо поддается рекурсивному определению, что тексты по программированию почти всегда включают его в качестве одного из первых примеров. Вы можете выразить определение n! рекурсивно вот так:

Как и в примере, показанном выше, существуют базовые случаи, которые разрешимы без рекурсии. Более сложные случаи являются редуктивными, что означает, что они сводятся к одному из базовых случаев:

• Базовые случаи (n = 0 или n = 1) разрешимы без рекурсии.
• Для значений n, превышающих 1, n! определяется в виде (n - 1)!, таким образом, рекурсивное решение постепенно приближается к базовому варианту.

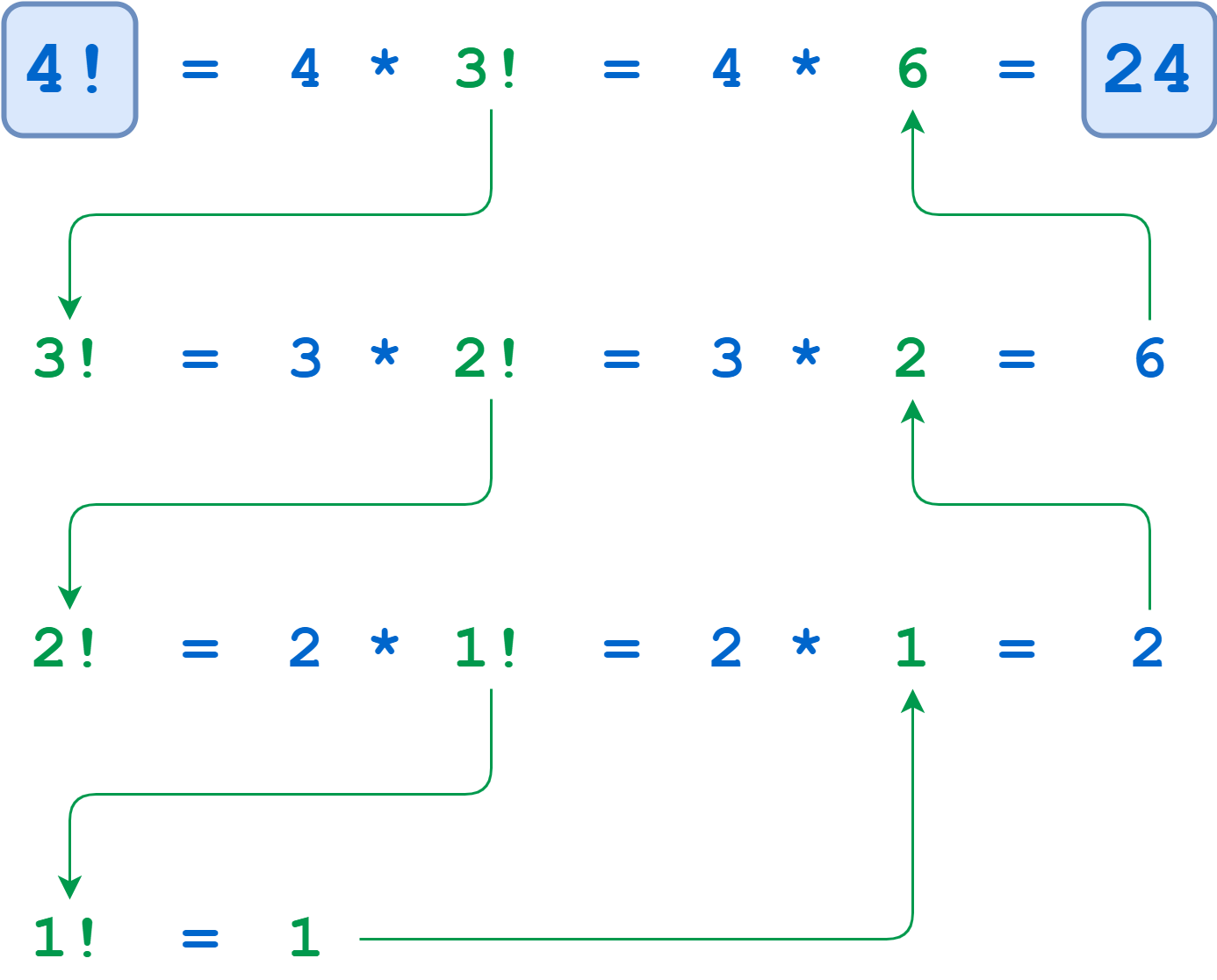
Например, рекурсивное вычисление 4! выглядит следующим образом:

Рекурсивное вычисление 4!

Вычисления 4!, 3! и 2! приостанавливаются до тех пор, пока алгоритм не достигнет базового варианта, где n = 1. В этот момент значение 1! вычислимо без дальнейшей рекурсии, и отложенные вычисления выполняются до завершения.

Определите факториальную функцию Python

Вот рекурсивная функция Python для вычисления факториала. Обратите внимание, насколько она лаконична и насколько хорошо отражает приведенное выше определение:

>>> def factorial(n):
...     return 1 if n <= 1 else n * factorial(n - 1)
...

>>> factorial(4)
24

Немного дополню эту функцию некоторыми инструкциями print(), которые дают более четкое представление о последовательности вызова и возврата:

>>> def factorial(n):
...     print(f"factorial() called with n = {n}")
...     return_value = 1 if n <= 1 else n * factorial(n -1)
...     print(f"-> factorial({n}) returns {return_value}")
...     return return_value
...

>>> factorial(4)
factorial() called with n = 4
factorial() called with n = 3
factorial() called with n = 2
factorial() called with n = 1
-> factorial(1) returns 1
-> factorial(2) returns 2
-> factorial(3) returns 6
-> factorial(4) returns 24
24

Обратите внимание, как все рекурсивные вызовы суммируются. Функция вызывается с помощью n = 4, 3, 2, и 1 последовательно, прежде чем какой-либо из вызовов вернется. Наконец, когда n равно 1, проблема может быть решена без дополнительной рекурсии. Затем каждый из накопленных рекурсивных вызовов разворачивается обратно, возвращая 1, 2, 6, и, наконец, 24 из самого внешнего вызова.

Рекурсия здесь не нужна. Вы могли бы реализовать factorial() итеративно, используя цикл for:

>>> def factorial(n):
...     return_value = 1
...     for i in range(2, n + 1):
...         return_value *= i
...     return return_value
...

>>> factorial(4)
24

Вы также можете реализовать факториал, используя Python reduce(),, который вы можете импортировать из модуля functools:

>>> from functools import reduce
>>> def factorial(n):
...     return reduce(lambda x, y: x * y, range(1, n + 1) or [1])
...

>>> factorial(4)
24

Опять же, это показывает, что если проблема разрешима с помощью рекурсии, то, скорее всего, также найдется несколько жизнеспособных нерекурсивных решений. Обычно вы выбираете, исходя из того, какой из них приводит к наиболее удобочитаемому и интуитивно понятному коду.

Еще одним фактором, который следует учитывать, является скорость выполнения. Между рекурсивными и нерекурсивными решениями могут быть существенные различия в производительности. В следующем разделе вы более подробно рассмотрите эти различия.

Сравнение скоростей реализации факториалов

Чтобы оценить время выполнения, вы можете использовать функцию с именем timeit() из модуля, который также называется timeit. Эта функция поддерживает несколько различных форматов, но в этом руководстве вы будете использовать следующий формат:

timeit(<command>, setup=<setup_string>, number=<iterations>)

timeit() сначала выполняет команды, содержащиеся в указанном <setup_string>. Затем он выполняет <command> заданное количество <iterations> и сообщает суммарное время выполнения в секундах:

>>> from timeit import timeit

>>> timeit("print(string)", setup="string='foobar'", number=100)
foobar
foobar
foobar
   .
   . [100 repetitions]
   .
foobar
0.03347089999988384

Здесь параметру setup присваивается string значение 'foobar'. Затем timeit() выводит string сто раз. Общее время выполнения составляет чуть более 3/100 секунды.

В примерах, показанных ниже, используется timeit() для сравнения рекурсивной, итеративной и reduce() реализаций factorial, описанных выше. В каждом случае setup_string содержит строку настройки, которая определяет соответствующую функцию factorial(). timeit() затем выполняет factorial(4) в общей сложности десять миллионов раз и сообщает о совокупном выполнении.

Во-первых, вот рекурсивная версия:

>>> setup_string = """
... print("Recursive:")
... def factorial(n):
...     return 1 if n <= 1 else n * factorial(n - 1)
... """

>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Recursive:
4.957105500000125

Далее следует итеративная реализация:

>>> setup_string = """
... print("Iterative:")
... def factorial(n):
...     return_value = 1
...     for i in range(2, n + 1):
...         return_value *= i
...     return return_value
... """

>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Iterative:
3.733752099999947

И последнее, вот версия, которая использует reduce():

>>> setup_string = """
... from functools import reduce
... print("reduce():")
... def factorial(n):
...     return reduce(lambda x, y: x * y, range(1, n + 1) or [1])
... """

>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
reduce():
8.101526299999932

В этом случае итеративная реализация является самой быстрой, хотя рекурсивное решение не сильно отстает. Метод, использующий reduce(), является самым медленным. Возможно, ваш опыт будет отличаться, если вы попробуете эти примеры на своем компьютере. Вы, конечно, не наберете одинаковое время и, возможно, даже не получите одинаковый рейтинг.

Имеет ли это значение? Разница во времени выполнения между итеративной реализацией и реализацией, использующей reduce(), составляет почти четыре секунды, но потребовалось десять миллионов вызовов, чтобы это увидеть.

Если вы будете вызывать функцию много раз, возможно, вам придется учитывать скорость выполнения при выборе реализации. С другой стороны, если функция будет запускаться относительно редко, то разница во времени выполнения, вероятно, будет незначительной. В этом случае вам лучше выбрать реализацию, которая, по-видимому, наиболее четко выражает решение проблемы.

Для факториала приведенные выше значения времени предполагают, что рекурсивная реализация является разумным выбором.

Честно говоря, если вы пишете на Python, вам вообще не нужно реализовывать факториальную функцию. Она уже доступна в стандартной math модуль:

>>> from math import factorial
>>> factorial(4)
24

Возможно, вам будет интересно узнать, как это работает в тесте синхронизации:

>>> setup_string = "from math import factorial"

>>> from timeit import timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
0.3724050999999946

Ничего себе! math.factorial() работает лучше, чем лучшая из трех других реализаций, показанных выше, примерно в 10 раз.

Техническое примечание: Тот факт, что math.factorial() намного быстрее, вероятно, не имеет никакого отношения к тому, реализован ли он рекурсивно. Скорее всего, это связано с тем, что функция реализована на C, а не на Python. Более подробную информацию о Python и C смотрите в этих ресурсах:

• Привязки к Python: Вызов C или C++ из Python
• Создание модуля расширения Python C
• C для программистов на Python
• Ваше руководство по исходному коду CPython
• Внутренние компоненты CPython книга

Функция, реализованная на C, практически всегда будет работать быстрее, чем соответствующая функция, реализованная на чистом Python.

Перемещение по вложенному списку

В следующем примере мы рассмотрим каждый элемент вложенной структуры списка. Рассмотрим следующий список на языке Python :

names = [
    "Adam",
    [
        "Bob",
        [
            "Chet",
            "Cat",
        ],
        "Barb",
        "Bert"
    ],
    "Alex",
    [
        "Bea",
        "Bill"
    ],
    "Ann"
]

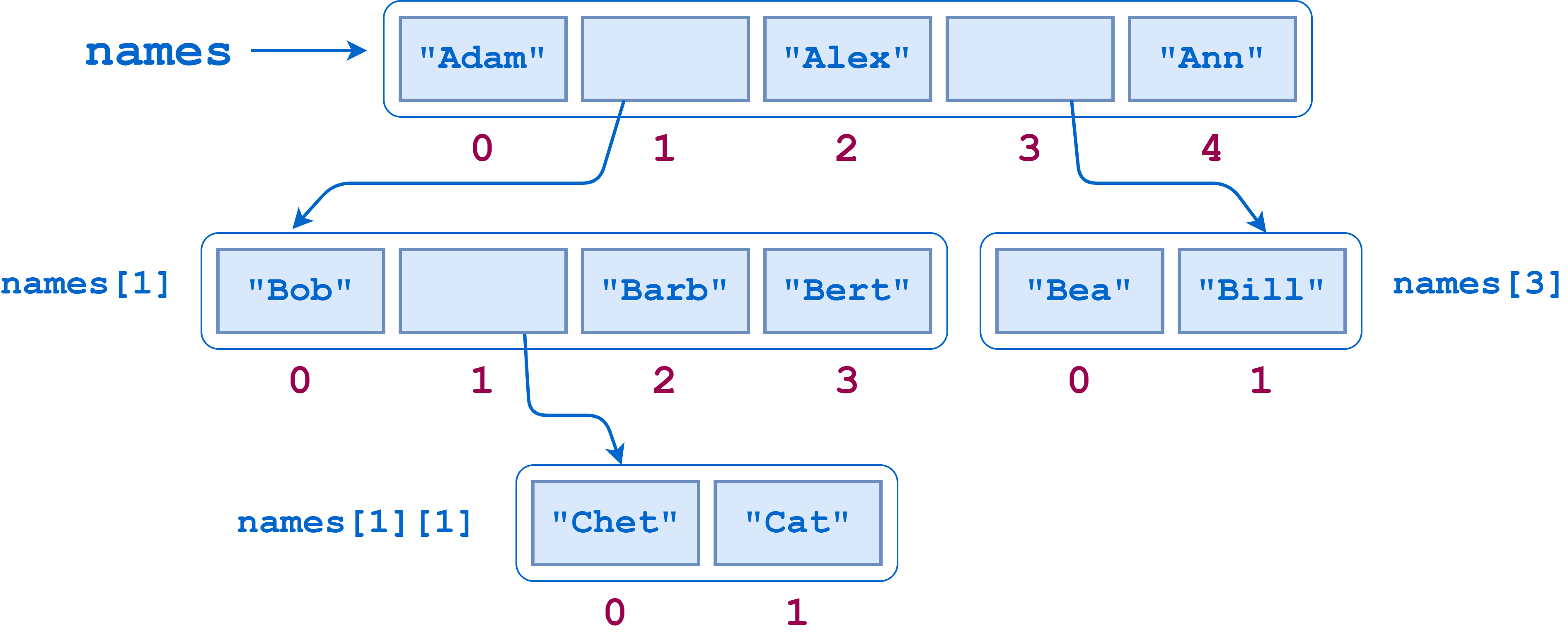
Как показано на следующей диаграмме, names содержит два подсписка. Первый из этих подсписков сам содержит другой подсписк:

Предположим, вы хотите подсчитать количество конечных элементов в этом списке — объектов самого низкого уровня str - как если бы вы выровняли список. Конечными элементами являются "Adam", "Bob", "Chet", "Cat", "Barb", "Bert", "Alex", "Bea", "Bill", и "Ann", поэтому ответ должен быть таким 10.

Простой вызов len() из списка не дает правильного ответа:

>>> len(names)
5

len() подсчитывает объекты на верхнем уровне names, которые являются тремя конечными элементами "Adam", "Alex", и "Ann" и двумя подсписками ["Bob", ["Chet", "Cat"], "Barb", "Bert"] и ["Bea", "Bill"]:

>>> for index, item in enumerate(names):
...     print(index, item)
...
0 Adam
1 ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert']
2 Alex
3 ['Bea', 'Bill']
4 Ann

Что вам нужно, так это функция, которая просматривает всю структуру списка, включая подсписки. Алгоритм выглядит примерно так:

1. Пройдитесь по списку, изучая каждый элемент по очереди.
2. Если вы найдете конечный элемент, добавьте его к общему количеству.
3. Если вы столкнулись с подсписком, выполните следующие действия:
   • Перейдите в этот подсписок и аналогично пройдитесь по нему.
   • Как только вы исчерпаете подсписок, вернитесь к нему, добавьте элементы из подсписка в накопленное количество и возобновите просмотр родительского списка с того места, где вы остановились.

Обратите внимание на самореферентный характер этого описания: Пройдитесь по списку. Если вы столкнулись с подсписком, то аналогичным образом пройдитесь по этому списку. Эта ситуация требует повторения!

Рекурсивный переход по вложенному списку

Рекурсия очень хорошо подходит для этой задачи. Чтобы решить ее, вам нужно уметь определять, является ли данный элемент списка конечным или нет. Для этого вы можете использовать встроенную функцию Python isinstance().

В случае списка names, если элемент является экземпляром типа list, то это подсписок. В противном случае это конечный элемент:

>>> names
['Adam', ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert'], 'Alex', ['Bea', 'Bill'], 'Ann']

>>> names[0]
'Adam'
>>> isinstance(names[0], list)
False

>>> names[1]
['Bob', ['Chet', 'Cat'], 'Barb', 'Bert']
>>> isinstance(names[1], list)
True

>>> names[1][1]
['Chet', 'Cat']
>>> isinstance(names[1][1], list)
True

>>> names[1][1][0]
'Chet'
>>> isinstance(names[1][1][0], list)
False

Теперь у вас есть инструменты для реализации функции, которая подсчитывает конечные элементы в списке, рекурсивно подсчитывая подсписки:

def count_leaf_items(item_list):
    """Recursively counts and returns the
       number of leaf items in a (potentially
       nested) list.
    """
    count = 0
    for item in item_list:
        if isinstance(item, list):
            count += count_leaf_items(item)
        else:
            count += 1

    return count

Если вы запустите count_leaf_items() в нескольких списках, включая список names, определенный выше, вы получите следующее:

>>> count_leaf_items([1, 2, 3, 4])
4
>>> count_leaf_items([1, [2.1, 2.2], 3])
4
>>> count_leaf_items([])
0

>>> count_leaf_items(names)
10
>>> # Success!

Как и в примере с факториалом, добавление некоторых инструкций print() помогает продемонстрировать последовательность рекурсивных вызовов и возвращает значений:

 1def count_leaf_items(item_list):
 2    """Recursively counts and returns the
 3       number of leaf items in a (potentially
 4       nested) list.
 5    """
 6    print(f"List: {item_list}")
 7    count = 0
 8    for item in item_list:
 9        if isinstance(item, list):
10            print("Encountered sublist")
11            count += count_leaf_items(item)
12        else:
13            print(f"Counted leaf item \"{item}\"")
14            count += 1
15
16    print(f"-> Returning count {count}")
17    return count

Вот краткое описание того, что происходит в приведенном выше примере:

• Строка 9: isinstance(item, list) равна True, значит, count_leaf_items() найден подсписок.
• Строка 11: Функция рекурсивно вызывает саму себя для подсчета элементов в подсписке, затем добавляет результат к общему количеству.
• Строка 12: isinstance(item, list) равна False, следовательно, count_leaf_items() столкнулся с конечным элементом.
• Строка 14: Функция увеличивает итоговую сумму на единицу для учета конечного элемента.

Примечание: Чтобы упростить задачу, в этой реализации предполагается, что список, передаваемый в count_leaf_items(), содержит только конечные элементы или подсписки, а не какой-либо другой тип составного объекта, такой как словарь или кортеж.

Результат count_leaf_items(), когда он выполняется в списке names, теперь выглядит следующим образом:

>>> count_leaf_items(names)
List: ['Adam', ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert'], 'Alex', ['Bea', 'Bill'], 'Ann']
Counted leaf item "Adam"
Encountered sublist
List: ['Bob', ['Chet', 'Cat'], 'Barb', 'Bert']
Counted leaf item "Bob"
Encountered sublist
List: ['Chet', 'Cat']
Counted leaf item "Chet"
Counted leaf item "Cat"
-> Returning count 2
Counted leaf item "Barb"
Counted leaf item "Bert"
-> Returning count 5
Counted leaf item "Alex"
Encountered sublist
List: ['Bea', 'Bill']
Counted leaf item "Bea"
Counted leaf item "Bill"
-> Returning count 2
Counted leaf item "Ann"
-> Returning count 10
10

Каждый раз, когда завершается вызов count_leaf_items(), он возвращает количество конечных элементов, которые он подсчитал в переданном ему списке. Вызов верхнего уровня возвращает 10, как и должно быть.

Нерекурсивный переход по вложенному списку

Как и в других примерах, показанных до сих пор, этот обход списка не требует рекурсии. Вы также можете выполнить его итеративно. Вот одна из возможностей:

def count_leaf_items(item_list):
    """Non-recursively counts and returns the
       number of leaf items in a (potentially
       nested) list.
    """
    count = 0
    stack = []
    current_list = item_list
    i = 0

    while True:
        if i == len(current_list):
            if current_list == item_list:
                return count
            else:
                current_list, i = stack.pop()
                i += 1
                continue

        if isinstance(current_list[i], list):
            stack.append([current_list, i])
            current_list = current_list[i]
            i = 0
        else:
            count += 1
            i += 1

Если вы запустите эту нерекурсивную версию count_leaf_items() в тех же списках, которые были показаны ранее, вы получите те же результаты:

>>> count_leaf_items([1, 2, 3, 4])
4
>>> count_leaf_items([1, [2.1, 2.2], 3])
4
>>> count_leaf_items([])
0

>>> count_leaf_items(names)
10
>>> # Success!

Используемая здесь стратегия использует стек для обработки вложенных подсписков. Когда эта версия count_leaf_items() обнаруживает подсписок, она помещает список, который выполняется в данный момент, и текущий индекс в этом списке в стек. После подсчета подсписка функция извлекает родительский список и индекс из стека, чтобы продолжить подсчет с того места, где он был прерван.

На самом деле, по сути, то же самое происходит и в рекурсивной реализации. Когда вы вызываете функцию рекурсивно, Python сохраняет состояние исполняемого экземпляра в стеке, чтобы рекурсивный вызов мог выполняться. Когда рекурсивный вызов завершается, состояние извлекается из стека, чтобы прерванный экземпляр мог возобновить работу. Это та же концепция, но с рекурсивным решением Python выполняет работу по сохранению состояния за вас.

Обратите внимание, насколько лаконичен и удобочитаем рекурсивный код по сравнению с нерекурсивной версией:

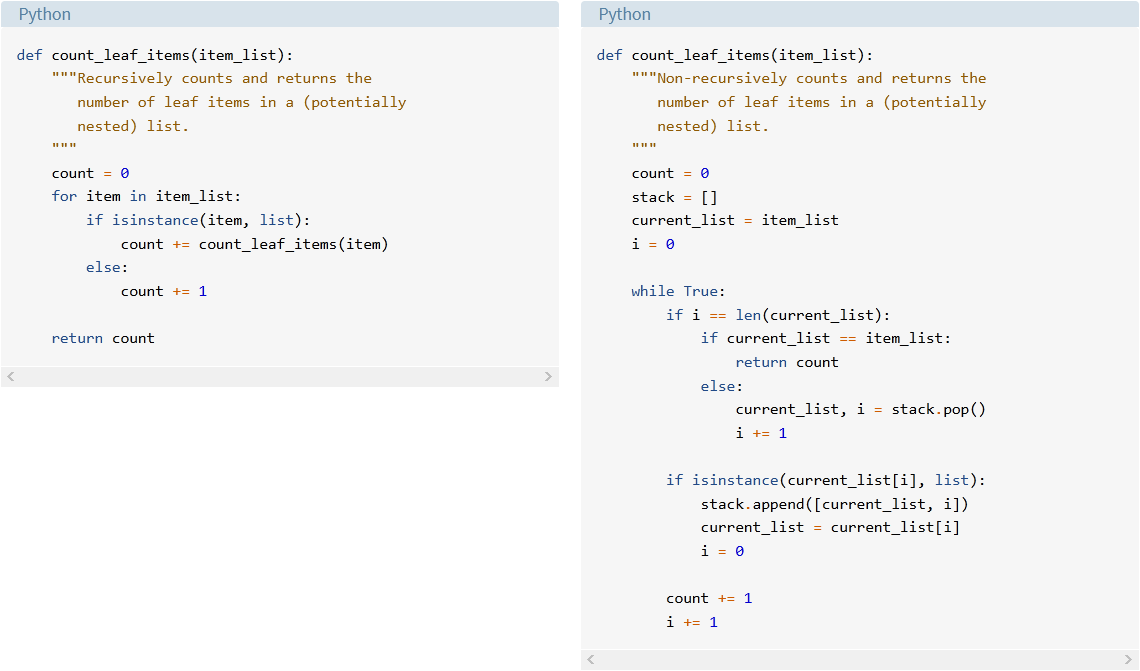Рекурсивный и нерекурсивный обход вложенных списков

Это тот случай, когда использование рекурсии определенно является преимуществом.

Обнаружение палиндромов

Выбор того, использовать ли рекурсию для решения задачи, во многом зависит от характера проблемы. Факториал, например, естественным образом переводится в рекурсивную реализацию, но итеративное решение также довольно простое. В таком случае, это, возможно, жеребьевка.

Проблема обхода списка - это совсем другая история. В этом случае рекурсивное решение очень элегантно, в то время как нерекурсивное в лучшем случае громоздко.

В следующей задаче использовать рекурсию, возможно, глупо.

Палиндром - это слово, которое читается как в обратном направлении, так и в прямом. В качестве примеров можно привести следующие слова:

• Гоночный автомобиль
• Уровень
• Каяк
• Возрождающий
• Гражданский

Если вас попросят разработать алгоритм для определения того, является ли строка палиндромной, вы, вероятно, предложите что-то вроде “Переверните строку и посмотрите, совпадает ли она с исходной”. Вы не можете выразиться намного яснее, чем это.

Что еще более полезно, синтаксис [::-1] в Python для преобразования строки в другую форму предоставляет удобный способ ее кодирования:

>>> def is_palindrome(word):
...     """Return True if word is a palindrome, False if not."""
...     return word == word[::-1]
...

>>> is_palindrome("foo")
False
>>> is_palindrome("racecar")
True
>>> is_palindrome("troglodyte")
False
>>> is_palindrome("civic")
True

Это ясно и лаконично. Вряд ли есть необходимость искать альтернативу. Но просто ради интереса рассмотрим это рекурсивное определение палиндрома:

• Базовые варианты: Пустая строка и строка, состоящая из одного символа, по своей сути являются палиндромами.
• Редуктивная рекурсия: Строка длиной два или более является палиндромом, если она удовлетворяет обоим этим критериям:
  1. Первый и последний символы совпадают.
  2. Подстрока между первым и последним символами является палиндромом.

Нарезка и здесь - ваш друг. Для строки word индексация и нарезка дают следующие подстроки:

• Первый символ равен word[0].
• Последний символ равен word[-1].
• Подстрока между первым и последним символами является word[1:-1].

Таким образом, вы можете определить is_palindrome() рекурсивно следующим образом:

>>> def is_palindrome(word):
...     """Return True if word is a palindrome, False if not."""
...     if len(word) <= 1:
...         return True
...     else:
...         return word[0] == word[-1] and is_palindrome(word[1:-1])
...

>>> # Base cases
>>> is_palindrome("")
True
>>> is_palindrome("a")
True

>>> # Recursive cases
>>> is_palindrome("foo")
False
>>> is_palindrome("racecar")
True
>>> is_palindrome("troglodyte")
False
>>> is_palindrome("civic")
True

Это интересное упражнение - мыслить рекурсивно, даже когда в этом нет особой необходимости.

Сортировка с помощью функции Быстрой сортировки

Последний представленный пример, такой как обход вложенного списка, является хорошим примером проблемы, которая естественным образом предполагает рекурсивный подход. Алгоритм быстрой сортировки - это эффективный алгоритм сортировки, разработанный британским ученым-компьютерщиком Тони Хором в 1959 году.

Быстрая сортировка - это алгоритм "разделяй и властвуй". Предположим, у вас есть список объектов для сортировки. Сначала вы выбираете элемент в списке, который называется сводный элемент. Это может быть любой элемент в списке. Затем вы разбиваете список на два подсписка на основе сводного элемента и рекурсивно сортируете подсписки.

Алгоритм состоит из следующих этапов:

• Выберите сводный элемент.
• Разделите список на два подсписка:
  1. Те элементы, которые меньше, чем сводный элемент
  2. Те элементы, которые больше, чем сводный элемент
• Быстрая сортировка подсписков рекурсивно.

При каждом разбиении создаются подсписки меньшего размера, поэтому алгоритм является упрощенным. Базовые случаи возникают, когда подсписки либо пусты, либо содержат один элемент, поскольку они по своей сути отсортированы.

Выбор элемента сводной таблицы

Алгоритм быстрой сортировки будет работать независимо от того, какой элемент в списке является сводным. Но некоторые варианты лучше, чем другие. Помните, что при разбиении на разделы создаются два подсписка: один с элементами, размер которых меньше, чем у сводного элемента, и другой с элементами, размер которых больше, чем у сводного элемента. В идеале эти два подсписка должны быть примерно одинаковой длины.

Представьте, что ваш первоначальный список для сортировки содержит восемь элементов. Если в результате каждого разбиения получаются подсписки примерно одинаковой длины, то вы можете перейти к базовым вариантам в три этапа:

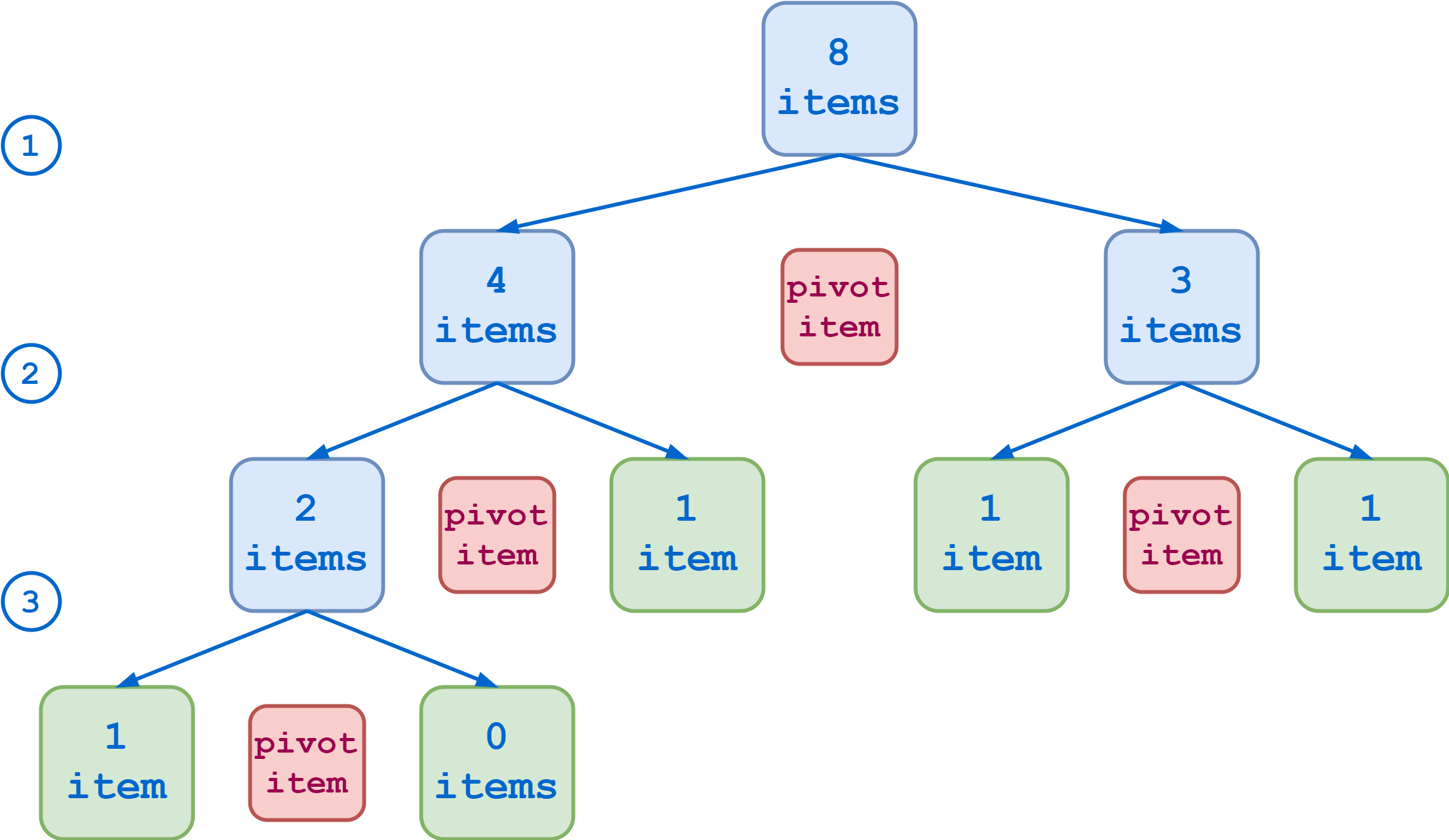Оптимальное разделение, список из восьми элементов

С другой стороны, если ваш выбор сводного элемента особенно неудачен, в результате каждого раздела получается один подсписок, содержащий все исходные элементы, кроме сводного элемента, и еще один подсписок, который пуст. В этом случае требуется выполнить семь шагов, чтобы свести список к базовым вариантам:

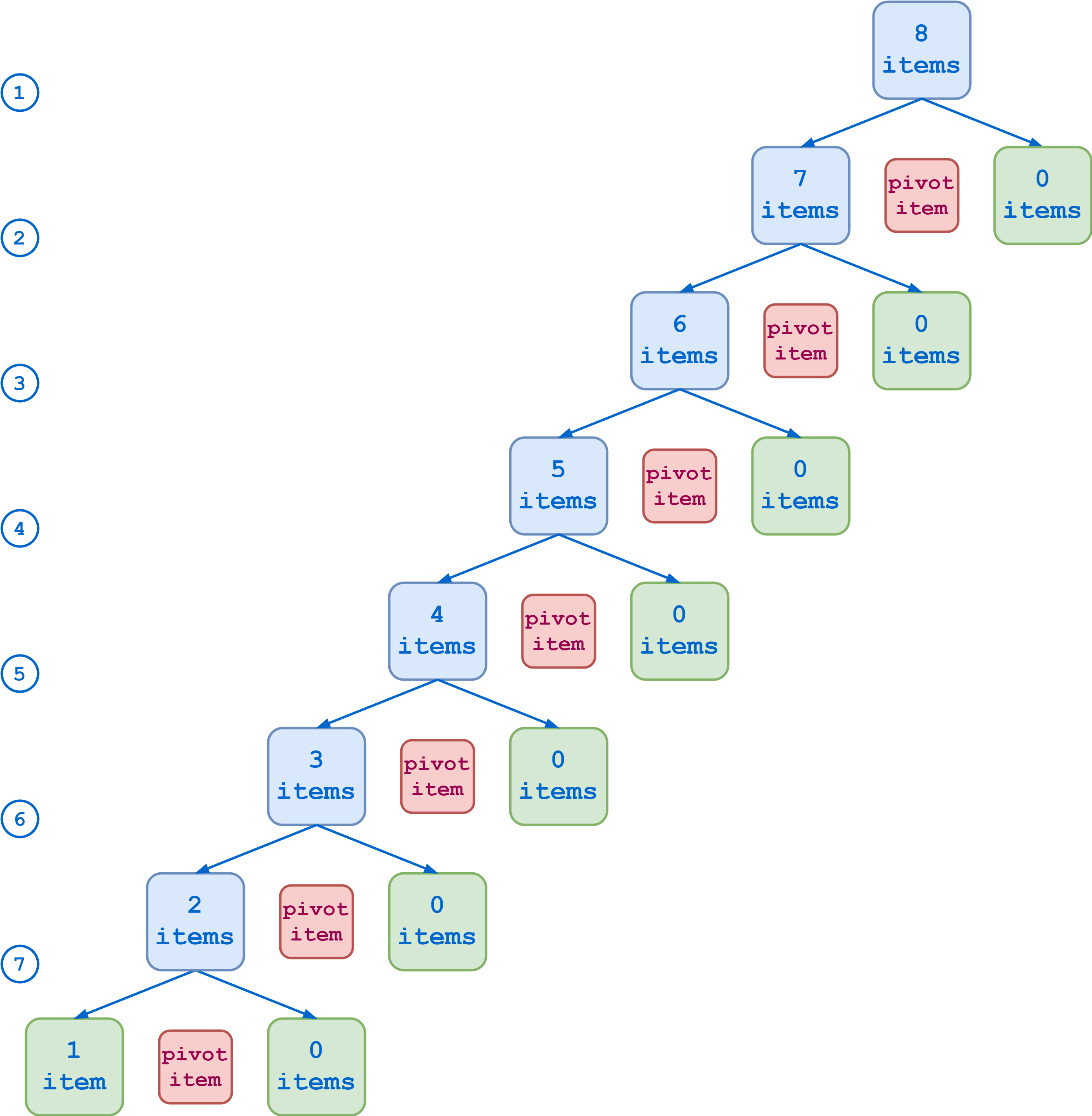Неоптимальное разделение, список из восьми элементов

В первом случае алгоритм быстрой сортировки будет более эффективным. Но вам нужно заранее знать кое-что о характере сортируемых данных, чтобы систематически выбирать оптимальные элементы сводки. В любом случае, не существует какого-то одного варианта, который был бы лучшим для всех случаев. Поэтому, если вы пишете функцию быстрой сортировки для обработки общего случая, выбор сводного элемента является несколько произвольным.

Первый элемент в списке является обычным выбором, как и последний элемент. Они будут работать нормально, если данные в списке распределены достаточно случайным образом. Однако, если данные уже отсортированы или даже почти отсортированы, это приведет к неоптимальному разбиению на разделы, как показано выше. Чтобы избежать этого, некоторые алгоритмы быстрой сортировки выбирают средний элемент в списке в качестве сводного элемента.

Другой вариант - найти медиану первого, последнего и среднего элементов в списке и использовать ее в качестве сводного элемента. Это стратегия, используемая в примере кода ниже.

Реализация секционирования

После того как вы выбрали сводный элемент, следующим шагом будет разбиение списка на разделы. Опять же, цель состоит в том, чтобы создать два подсписка, один из которых содержит элементы, которые меньше сводного элемента, а другой - те, которые больше.

Вы могли бы выполнить это непосредственно на месте. Другими словами, меняя местами элементы, вы можете перемещать элементы в списке до тех пор, пока сводный элемент не окажется посередине, все меньшие элементы - слева от него, а все большие элементы - справа. Затем, при рекурсивной быстрой сортировке подсписков, вы передадите фрагменты списка слева и справа от сводного элемента.

В качестве альтернативы, вы можете использовать возможности Python по манипулированию списками для создания новых списков вместо того, чтобы работать с исходным списком. Именно такой подход используется в приведенном ниже коде. Алгоритм следующий:

• Выберите опорный элемент, используя метод медианы из трех, описанный выше.
• Используя сводный элемент, создайте три подсписка:
  1. Элементы в исходном списке, которые меньше, чем сводный элемент
  2. Сам сводный элемент
  3. Элементы в исходном списке, которые больше, чем сводный элемент
• Рекурсивно выполните быструю сортировку списков 1 и 3.
• Объедините все три списка вместе.

Обратите внимание, что для этого требуется создать третий подсписок, содержащий сам сводный элемент. Одним из преимуществ этого подхода является то, что он легко обрабатывает случай, когда сводный элемент появляется в списке более одного раза. В этом случае список 2 будет содержать более одного элемента.

Использование реализации быстрой сортировки

Теперь, когда основа заложена, вы готовы перейти к алгоритму быстрой сортировки. Вот код на Python:

 1import statistics
 2
 3def quicksort(numbers):
 4    if len(numbers) <= 1:
 5        return numbers
 6    else:
 7        pivot = statistics.median(
 8            [
 9                numbers[0],
10                numbers[len(numbers) // 2],
11                numbers[-1]
12            ]
13        )
14        items_less, pivot_items, items_greater = (
15            [n for n in numbers if n < pivot],
16            [n for n in numbers if n == pivot],
17            [n for n in numbers if n > pivot]
18        )
19
20        return (
21            quicksort(items_less) +
22            pivot_items +
23            quicksort(items_greater)
24        )

Вот что делает каждый раздел quicksort():

• Строка 4: Базовые случаи, когда список либо пуст, либо содержит только один элемент
• Строки с 7 по 13: Расчет сводного элемента методом медианы из трех
• Строки с 14 по 18: Создание трех списков разделов
• Строки с 20 по 24: Рекурсивная сортировка и повторная сборка списков разделов

Примечание: Преимущество этого примера в том, что он лаконичен и относительно удобочитаем. Однако это не самая эффективная реализация. В частности, создание списков разделов в строках с 14 по 18 требует выполнения трех отдельных итераций по списку, что не является оптимальным с точки зрения времени выполнения.

Вот несколько примеров quicksort() в действии:

>>> # Base cases
>>> quicksort([])
[]
>>> quicksort([42])
[42]

>>> # Recursive cases
>>> quicksort([5, 2, 6, 3])
[2, 3, 5, 6]
>>> quicksort([10, -3, 21, 6, -8])
[-8, -3, 6, 10, 21]

Для целей тестирования вы можете определить короткую функцию, которая генерирует список случайных чисел в диапазоне от 1 до 100:

import random

def get_random_numbers(length, minimum=1, maximum=100):
    numbers = []
    for _ in range(length):
        numbers.append(random.randint(minimum, maximum))

    return numbers

Теперь вы можете использовать get_random_numbers() для тестирования quicksort():

>>> numbers = get_random_numbers(20)
>>> numbers
[24, 4, 67, 71, 84, 63, 100, 94, 53, 64, 19, 89, 48, 7, 31, 3, 32, 76, 91, 78]
>>> quicksort(numbers)
[3, 4, 7, 19, 24, 31, 32, 48, 53, 63, 64, 67, 71, 76, 78, 84, 89, 91, 94, 100]

>>> numbers = get_random_numbers(15, -50, 50)
>>> numbers
[-2, 14, 48, 42, -48, 38, 44, -25, 14, -14, 41, -30, -35, 36, -5]
>>> quicksort(numbers)
[-48, -35, -30, -25, -14, -5, -2, 14, 14, 36, 38, 41, 42, 44, 48]

>>> quicksort(get_random_numbers(10, maximum=500))
[49, 94, 99, 124, 235, 287, 292, 333, 455, 464]
>>> quicksort(get_random_numbers(10, 1000, 2000))
[1038, 1321, 1530, 1630, 1835, 1873, 1900, 1931, 1936, 1943]

Чтобы лучше понять, как работает quicksort(), посмотрите на диаграмму ниже. Здесь показана последовательность рекурсии при сортировке списка из двенадцати элементов:

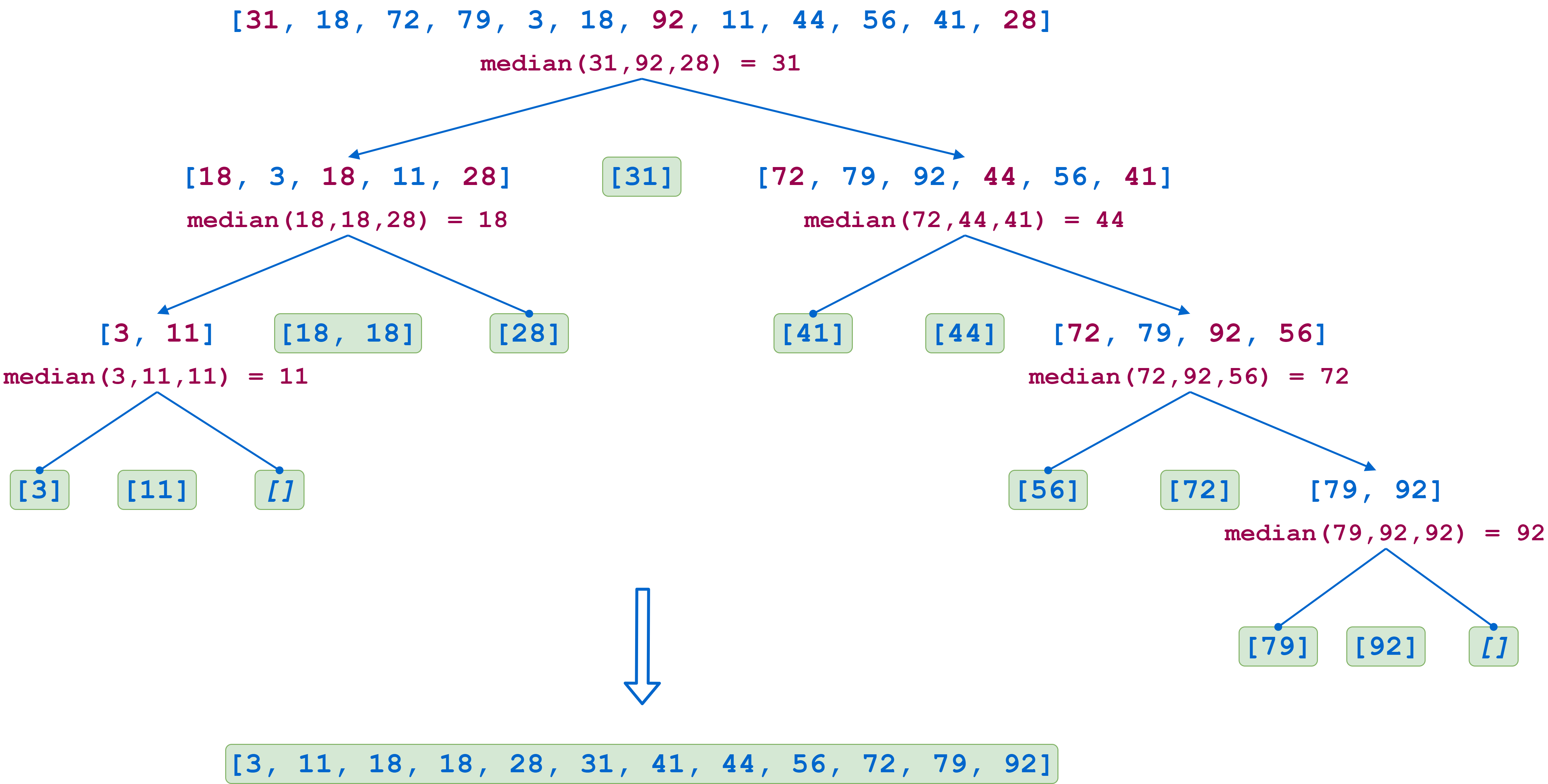Алгоритм быстрой сортировки, список из двенадцати элементов

На первом шаге первым, средним и последним значениями списка являются 31, 92, и 28 соответственно. Медиана равна 31, поэтому она становится сводным элементом. Затем первый раздел состоит из следующих подсписков:

Sublist	Items
[18, 3, 18, 11, 28]	The items less than the pivot item
[31]	The pivot item itself
[72, 79, 92, 44, 56, 41]	The items greater than the pivot item

Каждый подсписок впоследствии рекурсивно разбивается на разделы таким же образом, пока все подсписки либо не будут содержать один элемент, либо не станут пустыми. По мере выполнения рекурсивных вызовов списки будут повторно собраны в отсортированном порядке. Обратите внимание, что на предпоследнем шаге слева сводный элемент 18 появляется в списке дважды, поэтому список сводных элементов состоит из двух элементов.

Заключение

На этом ваше знакомство с рекурсией, техникой программирования, при которой функция вызывает саму себя, завершается. Рекурсия ни в коем случае не подходит для каждой задачи. Но некоторые проблемы программирования просто требуют этого. В таких ситуациях это отличный метод, который стоит иметь в своем распоряжении.

В этом уроке вы узнали:

• Что значит для функции вызывать саму себя рекурсивно
• Как дизайн функций Python поддерживает рекурсию
• Какие факторы следует учитывать при выборе того, следует ли решать задачу рекурсивно
• Как реализовать рекурсивную функцию в Python

Вы также увидели несколько примеров рекурсивных алгоритмов и сравнили их с соответствующими нерекурсивными решениями.

Теперь вы должны быть в состоянии распознать, когда требуется рекурсия, и быть готовы уверенно использовать ее, когда это необходимо! Если вы хотите узнать больше о рекурсии в Python, ознакомьтесь с Рекурсивное мышление в Python.

<статус завершения article-slug="python-рекурсия" class="btn-group mb-0" data-api-article-bookmark-url="/api/v1/articles/python-рекурсия/закладка/" data-api-article-статус завершения-url="/api/v1/articles/python-recursion/completion_status/"> <поделиться-кнопка bluesky-text="Интересная статья #Python от @realpython.com :" email-body="Ознакомьтесь с этой статьей о Python:%0A%0ARecursion в Python: Введение" email-subject="Статья на Python для вас" twitter-text="Интересная статья на Python от @realpython:" url="https://realpython.com/python-recursion/" url-title="Рекурсия в Python: введение">

Смотрите сейчас, к этому уроку прилагается соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным руководством, чтобы углубить свое понимание: Рекурсия в Python

Back to Top