Основы статистики Python: как описывать данные

Оглавление

• Понимание описательной статистики
  • Виды мер
  • Популяция и выборки
  • Выбросы
• Выбор библиотек статистики Python
• Начало работы со статистическими библиотеками Python
• Расчет описательной статистики
  • Показатели центральной тенденции
  • Показатели изменчивости
  • Краткое изложение описательной статистики
  • Меры корреляции между парами данных
• Работа с 2D-Данными
  • Оси
  • Фреймы данных
• Визуализация данных
  • Прямоугольные графики
  • Гистограммы
  • Круговые диаграммы
  • Столбчатые диаграммы
  • Графики X-Y
  • Тепловые карты
• Заключение

В эпоху больших данных и искусственного интеллекта, наука о данных и машинное обучение стали незаменимыми во многих областях науки и техники. Необходимым аспектом работы с данными является умение описывать, обобщать и представлять данные визуально. Библиотеки статистики Python - это всеобъемлющие, популярные и широко используемые инструменты, которые помогут вам в работе с данными.

В этом уроке вы узнаете:

• Какие числовые величины вы можете использовать для описания и обобщения ваших наборов данных
• Как вычислять описательную статистику на чистом Python
• Как получить описательную статистику с помощью доступных библиотек Python
• Как визуализировать ваши наборы данных

Понимание описательной статистики

Описательная статистика основана на описании и обобщении данных. В ней используются два основных подхода:

1. Количественный подход описывает и обобщает данные в численном виде.
2. Визуальный подход иллюстрирует данные с помощью диаграмм, графиков-построек, гистограмм и других графиков.

Вы можете применить описательную статистику к одному или нескольким наборам данных или переменным. Когда вы описываете и обобщаете одну переменную, вы выполняете одномерный анализ. Когда вы ищете статистические взаимосвязи между парой переменных, вы выполняете двумерный анализ. Аналогично, многомерный анализ имеет дело сразу с несколькими переменными.

Виды мер

В этом руководстве вы узнаете о следующих типах показателей в описательной статистике:

• Центральная тенденция указывает на центры данных. Полезными показателями являются среднее значение, медиана и модус.
• Вариабельность позволяет судить о разбросе данных. Полезными показателями являются дисперсия и стандартное отклонение.
• Корреляция или совместная изменчивость сообщает вам о связи между парой переменных в наборе данных. Полезные показатели включают ковариацию и коэффициент корреляции .

Вы узнаете, как понимать и вычислять эти показатели с помощью Python.

Популяция и выборки

В статистике совокупность - это набор всех интересующих вас элементов или позиций. Популяции часто бывают обширными, что делает их неподходящими для сбора и анализа данных. Вот почему статистики обычно пытаются сделать какие-то выводы о совокупности, выбирая и исследуя репрезентативную подгруппу этой совокупности.

Это подмножество совокупности называется выборкой. В идеале выборка должна в удовлетворительной степени сохранять основные статистические характеристики совокупности. Таким образом, вы сможете использовать выборку для составления выводов о популяции.

Выбросы

Выброс - это точка данных, которая значительно отличается от большинства данных, взятых из выборки или генеральной совокупности. Существует множество возможных причин выбросов, но для начала приведем несколько из них:

• Естественная изменчивость в данных
• Изменение в поведении наблюдаемой системы
• Ошибки при сборе данных

Ошибки при сборе данных являются особенно распространенной причиной отклонений. Например, ограничения измерительных приборов или процедур могут привести к тому, что правильные данные просто невозможно получить. Другие ошибки могут быть вызваны неправильными расчетами, загрязнением данных, человеческим фактором и многим другим.

Точного математического определения выбросов не существует. Вы должны полагаться на опыт, знания об интересующем вас предмете и здравый смысл, чтобы определить, является ли точка данных выбросом и как с этим справиться.

Выбор библиотек статистики Python

Существует множество статистических библиотек Python, с которыми вы можете работать, но в этом руководстве вы узнаете о некоторых из наиболее популярных и широко используемых из них:

• Python statistics - это встроенная библиотека Python для описательной статистики. Вы можете использовать его, если ваши наборы данных не слишком велики или если вы не можете полагаться на импорт других библиотек.

• NumPy - это сторонняя библиотека для численных вычислений, оптимизированная для работы с одномерными и многомерными массивами. Его основным типом является массив с именем ndarray. Эта библиотека содержит множество процедур для статистического анализа.

• SciPy - это сторонняя библиотека для научных вычислений, основанная на NumPy. Он предлагает дополнительные функциональные возможности по сравнению с NumPy, в том числе scipy.stats для статистического анализа.

• pandas - это сторонняя библиотека для численных вычислений, основанная на NumPy. Он отлично справляется с обработкой помеченных одномерных (1D) данных с помощью Series объектов и двумерных (2D) данных с помощью DataFrame объектов.

• Matplotlib - это сторонняя библиотека для визуализации данных. Он хорошо работает в сочетании с NumPy, SciPy и pandas.

Обратите внимание, что во многих случаях вместо массивов NumPy могут использоваться объекты Series и DataFrame. Часто вы можете просто передать их статистической функции NumPy или SciPy. Кроме того, вы можете получить немаркированные данные из Series или DataFrame в виде объекта np.ndarray, вызвав .values или .to_numpy().

Начало работы с библиотеками статистики Python

Встроенная библиотека Python statistics содержит относительно небольшое количество наиболее важных статистических функций. Официальная документация является ценным ресурсом для получения подробной информации. Если вы ограничены чистым Python, то библиотека Python statistics может быть правильным выбором.

Хорошим местом для начала изучения NumPy является официальное руководство пользователя , особенно краткое руководство пользователя и основные разделы. Официальная ссылка поможет вам освежить в памяти конкретные концепции NumPy. Во время чтения этого руководства вы, возможно, захотите ознакомиться с разделом статистика, а также с официальным справочником scipy.stats.

Примечание:

Чтобы узнать больше о NumPy, ознакомьтесь с этими ресурсами:

• Смотри, Мама, никаких for Циклов: Программирование массивов с помощью NumPy
• Очистка данных на Python с помощью pandas и NumPy
• NumPy arange(): Как использовать np.arange()

Если вы хотите изучить панд, то официальная страница "Начало работы" - отличное место для начала. Введение в структуры данных поможет вам ознакомиться с основными типами данных Series и DataFrame. Аналогичным образом, превосходное официальное вводное руководство призвано предоставить вам достаточно информации, чтобы начать эффективно использовать pandas на практике.

Примечание:

Чтобы узнать больше о пандах, ознакомьтесь с этими ресурсами:

• Использование pandas и Python для изучения вашего набора данных
• фреймы данных pandas 101
• Идиоматические панды: Хитрости и особенности, о которых вы, возможно, не знаете
• Быстрый, гибкий, простой и интуитивно понятный: Как ускорить ваши проекты pandas

matplotlib содержит исчерпывающее официальное руководство пользователя, с помощью которого вы можете ознакомиться с деталями использования библиотеки. Анатомия Matplotlib - отличный ресурс для начинающих, которые хотят начать работать с matplotlib и связанными с ним библиотеками.

Примечание:

Чтобы узнать больше о визуализации данных, ознакомьтесь с этими ресурсами:

• Построение графиков на Python с помощью Matplotlib (Руководство)
• Построение гистограммы на Python: NumPy, Matplotlib, pandas и Seaborn
• Интерактивная визуализация данных на Python с помощью Bokeh
• Построение графика с помощью pandas: визуализация данных на Python для начинающих

Давайте начнем использовать эти библиотеки статистики Python!

Расчет описательной статистики

Начните с импорта всех необходимых вам пакетов:

>>> import math
>>> import statistics
>>> import numpy as np
>>> import scipy.stats
>>> import pandas as pd

Это все пакеты, которые вам понадобятся для расчета статистики на Python. Обычно вы не используете встроенный в Python пакет math, но в этом руководстве он будет полезен. Позже вы импортируете matplotlib.pyplot для визуализации данных.

Давайте создадим некоторые данные для работы. Вы начнете со списков Python, содержащих произвольные числовые данные:

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> x_with_nan = [8.0, 1, 2.5, math.nan, 4, 28.0]
>>> x
[8.0, 1, 2.5, 4, 28.0]
>>> x_with_nan
[8.0, 1, 2.5, nan, 4, 28.0]

Теперь у вас есть списки x и x_with_nan. Они почти одинаковы, с той разницей, что x_with_nan содержит значение nan. Важно понимать поведение статистических процедур Python, когда они сталкиваются с не числовое значение (nan). В науке о данных часто встречаются пропущенные значения, и вы часто заменяете их на nan.

Примечание: Как получить значение nan?

В Python вы можете использовать любой из следующих способов:

• float('nan')
• math.nan
• np.nan

Вы можете использовать все эти функции взаимозаменяемо:

>>> math.isnan(np.nan), np.isnan(math.nan)
(True, True)
>>> math.isnan(y_with_nan[3]), np.isnan(y_with_nan[3])
(True, True)

Вы можете видеть, что все функции эквивалентны. Однако, пожалуйста, имейте в виду, что при сравнении двух значений nan на предмет равенства получается False. Другими словами, math.nan == math.nan является False!

Теперь создайте np.ndarray и pd.Series объекты, которые соответствуют x и x_with_nan:

>>> y, y_with_nan = np.array(x), np.array(x_with_nan)
>>> z, z_with_nan = pd.Series(x), pd.Series(x_with_nan)
>>> y
array([ 8. ,  1. ,  2.5, 4. , 28. ])
>>> y_with_nan
array([ 8. ,  1. ,  2.5,  nan,  4. , 28. ])
>>> z
0     8.0
1     1.0
2     2.5
3     4.0
4    28.0
dtype: float64
>>> z_with_nan
0     8.0
1     1.0
2     2.5
3     NaN
4     4.0
5    28.0
dtype: float64

Теперь у вас есть два массива NumPy (y и y_with_nan) и две панды ( Series (z и z_with_nan). Все это одномерные последовательности значений.

Примечание: Хотя в этом руководстве вы будете использовать списков, пожалуйста, имейте в виду, что в большинстве случаев вы можете использовать кортежи таким же образом.

Вы можете дополнительно указать метку для каждого значения в z и z_with_nan.

Показатели центральной тенденции

Показатели центральной тенденции показывают центральные или средние значения наборов данных. Существует несколько определений того, что считается центром набора данных. В этом руководстве вы узнаете, как определить и рассчитать следующие показатели центральной тенденции:

• Среднее значение
• Средневзвешенное значение
• Среднее геометрическое значение
• Среднее гармоническое значение
• Медиана
• Режим

Означает

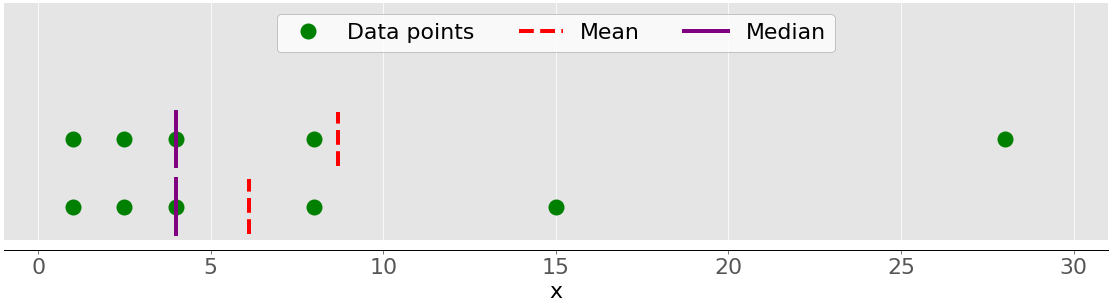
Выборочное среднее значение , также называемое выборочным средним арифметическим или просто средним значением, это среднее арифметическое значение всех элементов в наборе данных. Среднее значение набора данных θ математически выражается как σθ/θ, где 𝑖 = 1, 2, ..., 𝑛. Другими словами, это сумма всех элементов 𝑥ᵢ, деленная на количество элементов в наборе данных 𝑥.

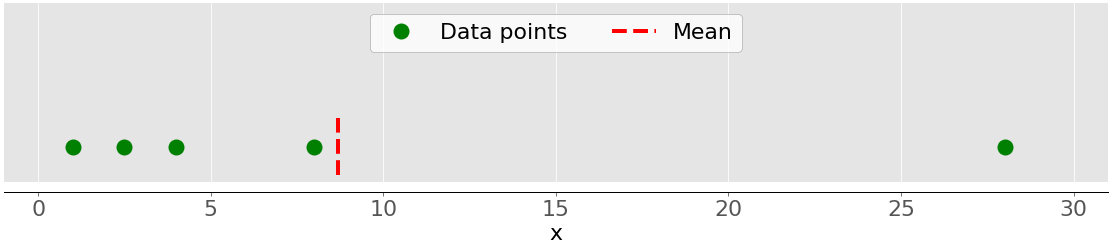
На этом рисунке показано среднее значение выборки с пятью точками данных:

Зеленые точки обозначают точки данных 1, 2,5, 4, 8 и 28. Красная пунктирная линия - это их среднее значение, или (1 + 2.5 + 4 + 8 + 28) / 5 = 8.7.

Вы можете рассчитать среднее значение с помощью чистого Python, используя sum() и len(), без импорта библиотек:

>>> mean_ = sum(x) / len(x)
>>> mean_
8.7

Хотя это чисто и элегантно, вы также можете применить встроенные статистические функции Python:

>>> mean_ = statistics.mean(x)
>>> mean_
8.7
>>> mean_ = statistics.fmean(x)
>>> mean_
8.7

Вы вызвали функции mean() и fmean() из встроенного Библиотека Python statistics и получили тот же результат, что и при использовании чистого Python. fmean() представлен в Python 3.8 как более быстрая альтернатива mean(). Он всегда возвращает число с плавающей запятой.

Однако, если среди ваших данных есть значения nan, то statistics.mean() и statistics.fmean() вернут nan в качестве выходных данных:

>>> mean_ = statistics.mean(x_with_nan)
>>> mean_
nan
>>> mean_ = statistics.fmean(x_with_nan)
>>> mean_
nan

Этот результат согласуется с поведением sum(), поскольку sum(x_with_nan) также возвращает nan.

Если вы используете NumPy, то вы можете получить среднее значение с помощью np.mean():

>>> mean_ = np.mean(y)
>>> mean_
8.7

В приведенном выше примере mean() является функцией, но вы также можете использовать соответствующий метод .mean():

>>> mean_ = y.mean()
>>> mean_
8.7

Функция mean() и метод .mean() из NumPy возвращают тот же результат, что и statistics.mean(). Это также относится к случаям, когда среди ваших данных есть значения nan:

>>> np.mean(y_with_nan)
nan
>>> y_with_nan.mean()
nan

Часто вам не нужно получать в результате значение nan. Если вы предпочитаете игнорировать значения nan, то вы можете использовать np.nanmean():

>>> np.nanmean(y_with_nan)
8.7

nanmean() просто игнорирует все значения nan. Возвращает то же значение, что и mean(), если вы применили его к набору данных без значений nan.

pd.Series у объектов также есть метод .mean():

>>> mean_ = z.mean()
>>> mean_
8.7

Как вы можете видеть, он используется так же, как и в случае с NumPy. Однако, .mean() из pandas по умолчанию игнорирует значения nan:

>>> z_with_nan.mean()
8.7

Такое поведение является результатом значения по умолчанию необязательного параметра skipna. Вы можете изменить этот параметр, чтобы изменить поведение.

Средневзвешенное значение

Средневзвешенное значение , также называемое взвешенным средним арифметическим значением или средневзвешенным значением, представляет собой обобщение среднего арифметического, которое позволяет определить относительный вклад каждой точки данных в результат.

ты определись один вес 𝑤ᵢ для каждой точки данных 𝑥ᵢ набора данных 𝑥, где 𝑖 = 1, 2, ..., 𝑛 и 𝑛 - число элементов в 𝑥. Затем вы умножаете каждую точку данных на соответствующий вес, суммируете все произведения и делите полученную сумму на сумму весов: σᵢ(𝑤ᵢ𝑥ᵢ) / σᵢ𝑤ᵢ.

Примечание: Удобно (и обычно так и бывает), что все веса неотрицательны, 𝑤ᵢ ≥ 0, и что их сумма равна единице, или σᵢ𝑤ᵢ = 1.

Средневзвешенное значение очень удобно, когда вам нужно среднее значение набора данных, содержащего элементы, которые встречаются с заданной относительной частотой. Например, предположим, что у вас есть набор, в котором 20% всех элементов равны 2, 50% элементов равны 4, а остальные 30% элементов равны 8. Вы можете вычислить среднее значение такого набора следующим образом:

>>> 0.2 * 2 + 0.5 * 4 + 0.3 * 8
4.8

Здесь вы учитываете частоты и веса. При использовании этого метода вам не нужно знать общее количество элементов.

Вы можете реализовать средневзвешенное значение на чистом Python, объединив sum() либо с range() , либо zip():

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> w = [0.1, 0.2, 0.3, 0.25, 0.15]
>>> wmean = sum(w[i] * x[i] for i in range(len(x))) / sum(w)
>>> wmean
6.95
>>> wmean = sum(x_ * w_ for (x_, w_) in zip(x, w)) / sum(w)
>>> wmean
6.95

Опять же, это чистая и элегантная реализация, в которой вам не нужно импортировать какие-либо библиотеки.

Однако, если у вас большие наборы данных, то NumPy, скорее всего, предложит лучшее решение. Вы можете использовать np.average() чтобы получить средневзвешенное значение для массивов NumPy или pandas Series:

>>> y, z, w = np.array(x), pd.Series(x), np.array(w)
>>> wmean = np.average(y, weights=w)
>>> wmean
6.95
>>> wmean = np.average(z, weights=w)
>>> wmean
6.95

Результат тот же, что и в случае реализации на чистом Python. Вы также можете использовать этот метод для обычных списков и кортежей.

Другим решением является использование поэлементного продукта w * y с np.sum() или .sum():

>>> (w * y).sum() / w.sum()
6.95

Вот и все! Вы рассчитали средневзвешенное значение.

Однако будьте осторожны, если ваш набор данных содержит значения nan:

>>> w = np.array([0.1, 0.2, 0.3, 0.0, 0.2, 0.1])
>>> (w * y_with_nan).sum() / w.sum()
nan
>>> np.average(y_with_nan, weights=w)
nan
>>> np.average(z_with_nan, weights=w)
nan

В этом случае average() возвращает nan, что согласуется с np.mean().

Среднее гармоническое значение

Среднее гармоническое значение равно значению, обратному среднему значению обратных значений всех элементов в наборе данных: 𝑛 / σᵢ(1/𝑥ᵢ), где 𝑖 = 1, 2, ..., 𝑛 и 𝑛 - это количество элементов в наборе данных 𝑥. Один из вариантов реализации гармонического среднего на чистом Python заключается в следующем:

>>> hmean = len(x) / sum(1 / item for item in x)
>>> hmean
2.7613412228796843

Это сильно отличается от среднего арифметического значения для тех же данных x, которое, по вашим расчетам, составляет 8,7.

Вы также можете рассчитать этот показатель с помощью statistics.harmonic_mean():

>>> hmean = statistics.harmonic_mean(x)
>>> hmean
2.7613412228796843

В приведенном выше примере показана одна из реализаций statistics.harmonic_mean(). Если в наборе данных есть значение nan, то оно вернет значение nan. Если есть хотя бы один 0, то он вернет 0. Если вы укажете хотя бы одно отрицательное число, то получите statistics.StatisticsError:

>>> statistics.harmonic_mean(x_with_nan)
nan
>>> statistics.harmonic_mean([1, 0, 2])
0
>>> statistics.harmonic_mean([1, 2, -2])  # Raises StatisticsError

Помните об этих трех сценариях, когда будете использовать этот метод!

Третий способ вычисления среднего гармонического значения заключается в использовании scipy.stats.hmean():

>>> scipy.stats.hmean(y)
2.7613412228796843
>>> scipy.stats.hmean(z)
2.7613412228796843

Опять же, это довольно простая реализация. Однако, если ваш набор данных содержит nan, 0, отрицательное число или что-либо еще, кроме положительных чисел, то вы получите ValueError!

Среднее геометрическое значение

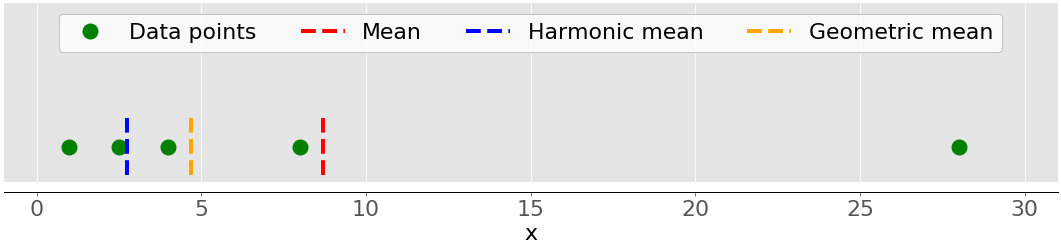
Этот среднее геометрическое - Это 𝑛-й корень из произведения все элементы 𝑛 𝑥 𝑥 ᵢ набора данных: ⁿ√(𝑥Πᵢ ᵢ), где 𝑖 = 1, 2, ..., 𝑛. На следующем рисунке показаны арифметические, гармонические и геометрические значения набора данных:

Опять же, зеленые точки обозначают точки данных 1, 2,5, 4, 8 и 28. Красная пунктирная линия - это среднее значение. Синяя пунктирная линия - это среднее гармоническое значение, а желтая пунктирная линия - среднее геометрическое значение.

Вы можете реализовать среднее геометрическое значение в чистом Python следующим образом:

>>> gmean = 1
>>> for item in x:
...     gmean *= item
...
>>> gmean **= 1 / len(x)
>>> gmean
4.677885674856041

Как вы можете видеть, значение среднего геометрического в данном случае существенно отличается от значений среднего арифметического (8,7) и гармонического (2,76) значений для того же набора данных x.

В Python 3.8 появился statistics.geometric_mean(),, который преобразует все значения в числа с плавающей запятой и возвращает их среднее геометрическое значение:

>>> gmean = statistics.geometric_mean(x)
>>> gmean
4.67788567485604

Вы получили тот же результат, что и в предыдущем примере, но с минимальной ошибкой округления.

Если вы передаете данные со значениями nan, то statistics.geometric_mean() будет вести себя как большинство аналогичных функций и вернет nan:

>>> gmean = statistics.geometric_mean(x_with_nan)
>>> gmean
nan

Действительно, это согласуется с поведением statistics.mean(), statistics.fmean(), и statistics.harmonic_mean(). Если среди ваших данных есть нулевое или отрицательное число, то statistics.geometric_mean() приведет к увеличению statistics.StatisticsError.

Вы также можете получить среднее геометрическое значение с помощью scipy.stats.gmean():

>>> scipy.stats.gmean(y)
4.67788567485604
>>> scipy.stats.gmean(z)
4.67788567485604

Вы получили тот же результат, что и при реализации на чистом Python.

Если в наборе данных есть значения nan, то gmean() вернет значение nan. Если есть хотя бы одно 0, то оно вернет 0.0 и выдаст предупреждение. Если вы укажете хотя бы одно отрицательное число, то получите nan и предупреждение.

Медиана

Медиана выборки является средним элементом отсортированного набора данных. Набор данных может быть отсортирован в порядке возрастания или убывания. Если число элементов 𝑛 в наборе данных нечетное, то медианой является значение в средней позиции: 0,5(𝑛 + 1). Если 𝑛 равно четному, то медиана - это среднее арифметическое двух значений в середине, то есть элементов в позициях 0,5𝑛 и 0.5𝑛 + 1.

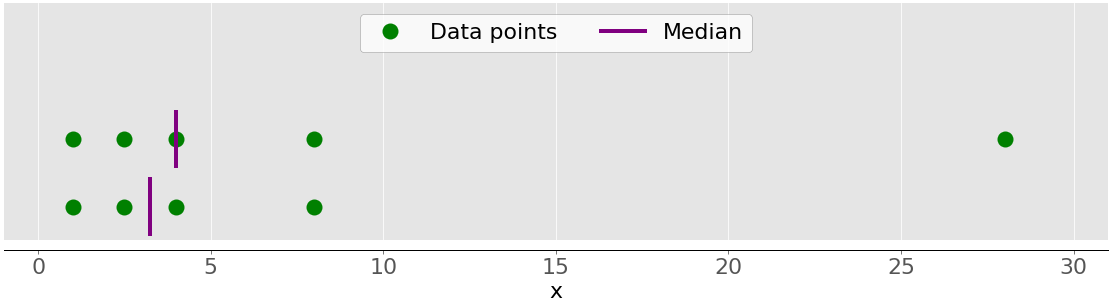
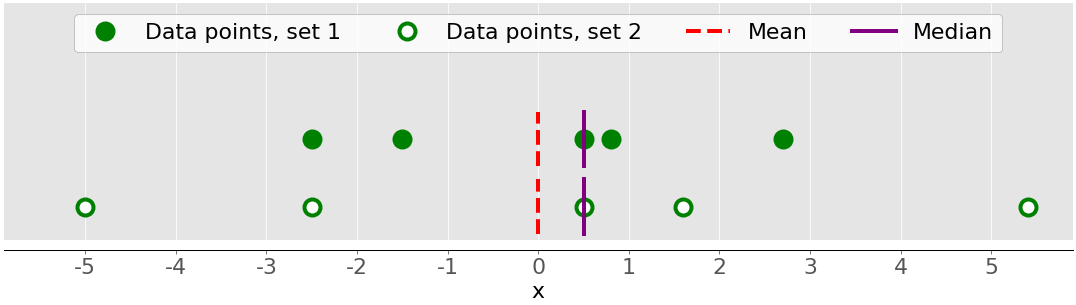
Например, если у вас есть точки данных 2, 4, 1, 8 и 9, то среднее значение равно 4, которое находится в середине отсортированного набора данных (1, 2, 4, 8, 9). Если точки данных равны 2, 4, 1 и 8, то медиана равна 3, что является средним значением двух средних элементов отсортированной последовательности (2 и 4). Это показано на следующем рисунке:

Точки данных обозначены зелеными точками, а фиолетовые линии показывают медиану для каждого набора данных. Среднее значение для верхнего набора данных (1, 2,5, 4, 8 и 28) равно 4. Если вы удалите выброс 28 из нижнего набора данных, то медиана станет средним арифметическим значением от 2,5 до 4, что равно 3,25.

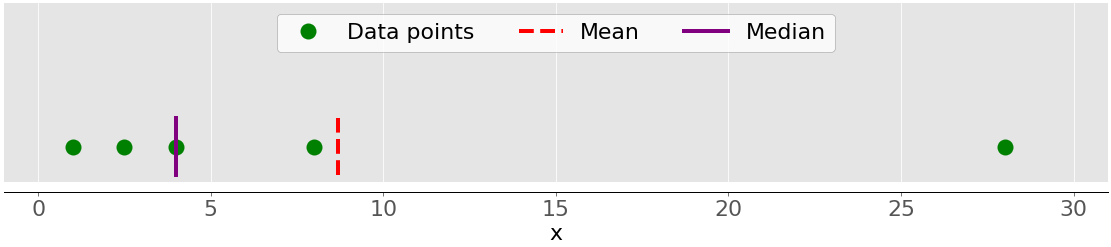
На рисунке ниже показаны среднее значение и медиана для точек данных 1, 2,5, 4, 8 и 28:

Опять же, среднее значение - это красная пунктирная линия, а медиана - фиолетовая линия.

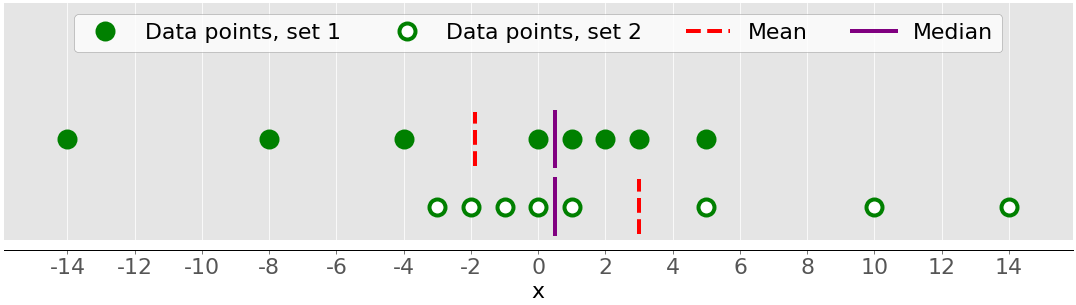
Основное различие между поведением среднего и медианы связано с набором данных выбросы или экстремумы. На среднее значение сильно влияют отклонения, но медиана зависит от них либо незначительно, либо вообще не зависит. Рассмотрим следующий рисунок:

Верхний набор данных снова содержит элементы 1, 2,5, 4, 8 и 28. Его среднее значение равно 8,7, а медиана равна 5, как вы видели ранее. Нижний набор данных показывает, что происходит, когда вы перемещаете крайнюю правую точку со значением 28:

• Если вы увеличите его значение (переместите вправо), то среднее значение увеличится, но медианное значение никогда не изменится.
• Если вы уменьшите его значение (переместите влево), то среднее значение уменьшится, но медиана останется неизменной до тех пор, пока значение движущейся точки не станет больше или равно 4.

Вы можете сравнить среднее значение и медиану как один из способов выявления отклонений и асимметрии в ваших данных. Что для вас полезнее - среднее значение или медиана, зависит от контекста вашей конкретной проблемы.

Вот одна из многих возможных реализаций медианы на чистом Python:

>>> n = len(x)
>>> if n % 2:
...     median_ = sorted(x)[round(0.5*(n-1))]
... else:
...     x_ord, index = sorted(x), round(0.5 * n)
...     median_ = 0.5 * (x_ord[index-1] + x_ord[index])
...
>>> median_
4

Двумя наиболее важными этапами этой реализации являются следующие:

1. Сортировка элементов набора данных
2. Поиск среднего элемента(ов) в отсортированном наборе данных

Вы можете получить медиану с помощью statistics.median():

>>> median_ = statistics.median(x)
>>> median_
4
>>> median_ = statistics.median(x[:-1])
>>> median_
3.25

Отсортированная версия x равна [1, 2.5, 4, 8.0, 28.0], поэтому элемент в середине равен 4. Отсортированная версия x[:-1], которая равна x без последнего элемента 28.0, равна [1, 2.5, 4, 8.0]. Итак, есть два средних элемента, 2.5 и 4. Их среднее значение равно 3.25.

median_low() и median_high() есть еще две функции, связанные с медианой в библиотеке Python statistics. Они всегда возвращают элемент из набора данных:

• Если число элементов нечетное, то существует одно среднее значение, поэтому эти функции ведут себя точно так же, как median().
• Если количество элементов четное, то есть два средних значения. В этом случае median_low() возвращает меньшее среднее значение, а median_high() - большее среднее значение.

Вы можете использовать эти функции точно так же, как вы бы использовали median():

>>> statistics.median_low(x[:-1])
2.5
>>> statistics.median_high(x[:-1])
4

Опять же, отсортированная версия x[:-1] равна [1, 2.5, 4, 8.0]. Два элемента в середине - это 2.5 (низкий уровень) и 4 (высокий уровень).

В отличие от большинства других функций из библиотеки Python statistics, median(), median_low(), и median_high() не возвращают nan, когда есть nan значения между точками данных:

>>> statistics.median(x_with_nan)
6.0
>>> statistics.median_low(x_with_nan)
4
>>> statistics.median_high(x_with_nan)
8.0

Остерегайтесь такого поведения, потому что это может быть не то, чего вы хотите!

Вы также можете получить медиану с помощью np.median():

>>> median_ = np.median(y)
>>> median_
4.0
>>> median_ = np.median(y[:-1])
>>> median_
3.25

Вы получили те же значения с помощью statistics.median() и np.median().

Однако, если в вашем наборе данных есть значение nan, то np.median() выдает RuntimeWarning и возвращает nan. Если такое поведение вам не подходит, вы можете использовать nanmedian() для игнорирования всех значений nan:

>>> np.nanmedian(y_with_nan)
4.0
>>> np.nanmedian(y_with_nan[:-1])
3.25

Полученные результаты такие же, как при использовании statistics.median() и np.median(), примененных к наборам данных x и y.

у объектов pandas Series есть метод .median(), который по умолчанию игнорирует значения nan:

>>> z.median()
4.0
>>> z_with_nan.median()
4.0

Поведение .median() соответствует поведению .mean() в pandas. Вы можете изменить это поведение с помощью необязательного параметра skipna.

Режим

Режим выборки - это значение в наборе данных, которое встречается чаще всего. Если нет ни одного такого значения, то набор является мультимодальным, поскольку он имеет несколько модальных значений. Например, в наборе, содержащем пункты 2, 3, 2, 8 и 12, число 2 является режимным, поскольку оно встречается дважды, в отличие от других элементов, которые встречаются только один раз.

Вот как вы можете получить этот режим с помощью чистого Python:

>>> u = [2, 3, 2, 8, 12]
>>> mode_ = max((u.count(item), item) for item in set(u))[1]
>>> mode_
2

Вы используете u.count(), чтобы получить количество повторений каждого элемента в u. Элемент с максимальным количеством повторений является режимом. Обратите внимание, что вам не обязательно использовать set(u). Вместо этого вы можете заменить его просто на u и выполнить итерацию по всему списку.

Примечание: set(u) возвращает Python набор со всеми уникальными элементами в u. Вы можете использовать этот трюк для оптимизации работы с большими данными, особенно если ожидаете увидеть много дубликатов.

Вы можете получить режим с помощью statistics.mode() и statistics.multimode():

>>> mode_ = statistics.mode(u)
>>> mode_
>>> mode_ = statistics.multimode(u)
>>> mode_
[2]

Как вы можете видеть, mode() возвращает одно значение, в то время как multimode() возвращает список, содержащий результат. Однако это не единственное различие между двумя функциями. Если существует более одного модального значения, то mode() вызывает StatisticsError, в то время как multimode() возвращает список со всеми режимами:

>>> v = [12, 15, 12, 15, 21, 15, 12]
>>> statistics.mode(v)  # Raises StatisticsError
>>> statistics.multimode(v)
[12, 15]

Вам следует обратить особое внимание на этот сценарий и быть осторожным при выборе между этими двумя функциями.

statistics.mode() и statistics.multimode() обрабатывают значения nan как обычные значения и могут возвращать nan как модальное значение:

>>> statistics.mode([2, math.nan, 2])
2
>>> statistics.multimode([2, math.nan, 2])
[2]
>>> statistics.mode([2, math.nan, 0, math.nan, 5])
nan
>>> statistics.multimode([2, math.nan, 0, math.nan, 5])
[nan]

В первом примере, приведенном выше, число 2 встречается дважды и является модальным значением. Во втором примере nan является модальным значением, поскольку оно встречается дважды, в то время как другие значения встречаются только один раз.

Примечание: statistics.multimode() введено в Python 3.8.

Вы также можете получить режим с помощью scipy.stats.mode():

>>> u, v = np.array(u), np.array(v)
>>> mode_ = scipy.stats.mode(u)
>>> mode_
ModeResult(mode=array([2]), count=array([2]))
>>> mode_ = scipy.stats.mode(v)
>>> mode_
ModeResult(mode=array([12]), count=array([3]))

Эта функция возвращает объект с модальным значением и количеством раз, когда оно встречается. Если в наборе данных имеется несколько модальных значений, то возвращается только наименьшее значение .

Вы можете получить режим и количество его вхождений в виде числовых массивов с точечной нотацией:

>>> mode_.mode
array([12])
>>> mode_.count
array([3])

Этот код использует .mode для возврата наименьшего значения режима (12) в массиве v и .count для возврата количества раз, когда это происходит (3). scipy.stats.mode() также является гибким при использовании значений nan. Это позволяет вам определить желаемое поведение с помощью необязательного параметра nan_policy. Этот параметр может принимать значения 'propagate', 'raise' ( ошибка), или 'omit'.

у объектов pandas Series есть метод .mode(), который хорошо обрабатывает мультимодальные значения и по умолчанию игнорирует значения nan:

>>> u, v, w = pd.Series(u), pd.Series(v), pd.Series([2, 2, math.nan])
>>> u.mode()
0    2
dtype: int64
>>> v.mode()
0    12
1    15
dtype: int64
>>> w.mode()
0    2.0
dtype: float64

Как вы можете видеть, .mode() возвращает новый pd.Series, который содержит все модальные значения. Если вы хотите, чтобы .mode() учитывали значения nan, просто передайте необязательный аргумент dropna=False.

Показатели изменчивости

Показателей центральной тенденции недостаточно для описания данных. Вам также понадобятся показатели изменчивости, которые количественно определяют разброс точек данных. В этом разделе вы узнаете, как определить и рассчитать следующие показатели изменчивости:

• Дисперсия
• Стандартное отклонение
• Асимметрия
• Процентили
• Диапазоны

Отклонение

Выборочная дисперсия количественно отражает разброс данных. Она показывает численно, насколько далеко точки данных находятся от среднего значения. Вы можете выразить дисперсию выборки из набора данных с 𝑥 𝑛 элементов математически как 𝑠2 = Σᵢ(𝑥ᵢ − значит(𝑥))2 / (𝑛 − 1), где 𝑖 = 1, 2, ..., 𝑛 и среднее(𝑥) является выборочной средней от 𝑥. Если вы хотите глубже понять, почему вы делите сумму на 𝑛 − 1 вместо 𝑛, тогда вы можете глубже погрузиться в Поправку Бесселя.

На следующем рисунке показано, почему важно учитывать дисперсию при описании наборов данных:

На этом рисунке представлены два набора данных:

1. Зеленые точки: Этот набор данных имеет меньшую дисперсию или меньшее среднее отличие от среднего значения. Он также имеет меньший диапазон или меньшую разницу между самым большим и самым маленьким товаром.
2. Белые точки: Этот набор данных имеет большую дисперсию или большее среднее отличие от среднего значения. Он также имеет больший ассортимент или большую разницу между самым большим и самым маленьким товаром.

Обратите внимание, что эти два набора данных имеют одинаковое среднее значение и медиану, хотя они, по-видимому, существенно различаются. Ни среднее, ни медиана не могут описать эту разницу. Вот почему вам нужны показатели вариабельности.

Вот как вы можете рассчитать дисперсию выборки с помощью чистого Python:

>>> n = len(x)
>>> mean_ = sum(x) / n
>>> var_ = sum((item - mean_)**2 for item in x) / (n - 1)
>>> var_
123.19999999999999

Этого подхода достаточно, и он хорошо вычисляет дисперсию выборки. Однако более коротким и элегантным решением является вызов существующей функции statistics.variance():

>>> var_ = statistics.variance(x)
>>> var_
123.2

Вы получили тот же результат для дисперсии, что и выше. variance() можно избежать вычисления среднего значения, если явно указать его в качестве второго аргумента: statistics.variance(x, mean_).

Если среди ваших данных есть значения nan, то будет возвращено значение statistics.variance() nan:

>>> statistics.variance(x_with_nan)
nan

Такое поведение согласуется с mean() и большинством других функций из библиотеки Python statistics.

Вы также можете рассчитать дисперсию выборки с помощью NumPy. Вам следует использовать функцию np.var() или соответствующий метод .var():

>>> var_ = np.var(y, ddof=1)
>>> var_
123.19999999999999
>>> var_ = y.var(ddof=1)
>>> var_
123.19999999999999

Очень важно указать параметр ddof=1. Таким образом вы устанавливаете дельта-степеней свободы на 1. Этот параметр позволяет правильно рассчитать значение 𝑠2, указав (𝑛 − 1) в знаменателе вместо 𝑛.

Если в наборе данных есть значения nan, то будут возвращены значения np.var() и .var() nan:

>>> np.var(y_with_nan, ddof=1)
nan
>>> y_with_nan.var(ddof=1)
nan

Это согласуется с np.mean() и np.average(). Если вы хотите пропустить значения nan, то вам следует использовать np.nanvar():

>>> np.nanvar(y_with_nan, ddof=1)
123.19999999999999

np.nanvar() игнорирует значения nan. Также необходимо указать ddof=1.

pd.Series у объектов есть метод .var(), который по умолчанию пропускает nan значений:

>>> z.var(ddof=1)
123.19999999999999
>>> z_with_nan.var(ddof=1)
123.19999999999999

У него также есть параметр ddof, но его значение по умолчанию равно 1, поэтому вы можете его опустить. Если вам нужно другое поведение, связанное со значениями nan, используйте необязательный параметр skipna.

Вы вычисляете дисперсию популяции аналогично дисперсии выборки. Однако, вы должны использовать 𝑛 в знаменателе вместо 𝑛 − 1: Σᵢ(𝑥ᵢ − означает(𝑥))2 / 𝑛. В этом случае, 𝑛 - число единиц в совокупности. Вы можете получить дисперсию генеральной совокупности, аналогичную дисперсии выборки, со следующими отличиями:

• Замените (n - 1) на n в реализации на чистом Python.
• Используйте statistics.pvariance() вместо statistics.variance().
• Укажите параметр ddof=0, если вы используете NumPy или pandas. В NumPy вы можете опустить ddof, потому что его значение по умолчанию равно 0.

Обратите внимание, что при расчете дисперсии вы всегда должны осознавать, работаете ли вы с выборкой или со всей совокупностью!

Стандартное отклонение

Стандартное отклонение выборки является еще одним показателем разброса данных. Оно связано с дисперсией выборки, поскольку стандартное отклонение, 𝑠, является положительным квадратным корнем из дисперсии выборки. Стандартное отклонение часто более удобно, чем дисперсия, поскольку оно имеет ту же единицу измерения, что и точки данных. Как только вы получите дисперсию, вы можете рассчитать стандартное отклонение с помощью чистого Python:

>>> std_ = var_ ** 0.5
>>> std_
11.099549540409285

Хотя это решение работает, вы также можете использовать statistics.stdev():

>>> std_ = statistics.stdev(x)
>>> std_
11.099549540409287

Конечно, результат тот же, что и раньше. Например, variance(), stdev() не вычисляет среднее значение, если вы явно указываете его в качестве второго аргумента: statistics.stdev(x, mean_).

Вы можете получить стандартное отклонение с помощью NumPy почти таким же образом. Вы можете использовать функцию std() и соответствующий метод .std() для вычисления стандартного отклонения. Если в наборе данных есть значения nan, то они вернут значение nan. Чтобы игнорировать значения nan, вы должны использовать np.nanstd(). Вы используете std(), .std(), и nanstd() из NumPy так же, как вы бы использовали var(), .var(), и nanvar():

>>> np.std(y, ddof=1)
11.099549540409285
>>> y.std(ddof=1)
11.099549540409285
>>> np.std(y_with_nan, ddof=1)
nan
>>> y_with_nan.std(ddof=1)
nan
>>> np.nanstd(y_with_nan, ddof=1)
11.099549540409285

Не забудьте установить дельта-степени свободы равными 1!

pd.Series у объектов также есть метод .std(), который по умолчанию пропускает nan:

>>> z.std(ddof=1)
11.099549540409285
>>> z_with_nan.std(ddof=1)
11.099549540409285

Параметр ddof по умолчанию имеет значение 1, поэтому вы можете его опустить. Опять же, если вы хотите обработать значения nan по-другому, то примените параметр skipna.

Стандартное отклонение популяции относится ко всей популяции. Это положительный квадратный корень из дисперсии популяции. Вы можете рассчитать его точно так же, как стандартное отклонение выборки, со следующими отличиями:

• Найдите квадратный корень из дисперсии популяции в реализации pure Python.
• Используйте statistics.pstdev() вместо statistics.stdev().
• Укажите параметр ddof=0, если вы используете NumPy или pandas. В NumPy вы можете опустить ddof, потому что его значение по умолчанию равно 0.

Как вы можете видеть, вы можете определить стандартное отклонение в Python, NumPy и pandas почти таким же образом, как вы определяете дисперсию. Вы используете разные, но аналогичные функции и методы с одинаковыми аргументами.

Асимметрия

Асимметрия выборки измеряет асимметрию выборки данных.

Существует несколько математических определений асимметрии. Одним из распространенных выражений для вычисления асимметрии набора данных 𝑥 с 𝑛 элементами является (𝑛2 / ((𝑛 − 1)(𝑛 − 2))) (σᵢ(𝑥ᵢ - среднее значение(𝑥))3 / (𝑛𝑠3)). Упростить выражение Σᵢ(𝑥ᵢ − значит(𝑥))3 𝑛 / ((𝑛 − 1)(𝑛 − 2)𝑠3), где 𝑖 = 1, 2, ..., 𝑛 и среднее(𝑥) является выборочной средней от 𝑥. Асимметрия, определенная таким образом, называется скорректированным стандартизированным коэффициентом момента Фишера-Пирсона.

На предыдущем рисунке были показаны два набора данных, которые были довольно симметричными. Другими словами, их точки находились на одинаковом расстоянии от среднего значения. В отличие от этого, на следующем рисунке показаны два асимметричных набора данных:

Первый набор представлен зелеными точками, а второй - белыми. Обычно значения отрицательной асимметрии указывают на наличие доминирующего хвоста с левой стороны, который вы можете увидеть при первом наборе. Положительные значения асимметрии соответствуют более длинный или толстый хвост с правой стороны, который вы можете увидеть во втором наборе. Если асимметрия близка к 0 (например, от -0,5 до 0,5), то набор данных считается достаточно симметричным.

После того, как вы рассчитали размер вашего набора данных n, среднее значение выборки mean_ и стандартное отклонение std_, вы можете получить асимметрию выборки с помощью чистого Python:

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> n = len(x)
>>> mean_ = sum(x) / n
>>> var_ = sum((item - mean_)**2 for item in x) / (n - 1)
>>> std_ = var_ ** 0.5
>>> skew_ = (sum((item - mean_)**3 for item in x)
...          * n / ((n - 1) * (n - 2) * std_**3))
>>> skew_
1.9470432273905929

Асимметрия положительная, поэтому x имеет хвост с правой стороны.

Вы также можете рассчитать асимметрию выборки с помощью scipy.stats.skew():

>>> y, y_with_nan = np.array(x), np.array(x_with_nan)
>>> scipy.stats.skew(y, bias=False)
1.9470432273905927
>>> scipy.stats.skew(y_with_nan, bias=False)
nan

Полученный результат совпадает с реализацией на чистом Python. Параметру bias присвоено значение False, позволяющее корректировать статистическую погрешность. Необязательный параметр nan_policy может принимать значения 'propagate', 'raise', или 'omit'. Он позволяет вам управлять тем, как вы будете обрабатывать значения nan.

у объектов pandas Series есть метод .skew(), который также возвращает асимметрию набора данных:

>>> z, z_with_nan = pd.Series(x), pd.Series(x_with_nan)
>>> z.skew()
1.9470432273905924
>>> z_with_nan.skew()
1.9470432273905924

Как и другие методы, .skew() по умолчанию игнорирует значения nan из-за значения необязательного параметра по умолчанию skipna.

Процентили

Выборочный 𝑝 процентиль - это элемент в наборе данных, у которого 𝑝% элементов в наборе данных меньше или равно этому значению. Кроме того, (100 − 𝑝)% элементов больше или равны этому значению. Если в наборе данных есть два таких элемента, то выборочный процентиль 𝑝 является их средним арифметическим значением. Каждый набор данных содержит три квартиля, которые являются процентилями, делящими набор данных на четыре части:

• Первый квартиль - это 25-й процентиль выборки. Это отделяет примерно 25% самых маленьких элементов от остального набора данных.
• Второй квартиль - это 50-й процентиль выборки или медиана . Примерно 25% товаров находятся между первым и вторым квартилями и еще 25% - между вторым и третьим квартилями.
• Третий квартиль - это 75-й процентиль выборки. Он отделяет примерно 25% самых крупных элементов от остальной части набора данных.

Каждая часть содержит примерно одинаковое количество элементов. Если вы хотите разделить ваши данные на несколько интервалов, то вы можете использовать statistics.quantiles():

>>> x = [-5.0, -1.1, 0.1, 2.0, 8.0, 12.8, 21.0, 25.8, 41.0]
>>> statistics.quantiles(x, n=2)
[8.0]
>>> statistics.quantiles(x, n=4, method='inclusive')
[0.1, 8.0, 21.0]

В этом примере 8.0 является медианой x, в то время как 0.1 и 21.0 являются выборочными 25-м и 75-м процентилями соответственно. Параметр n определяет количество результирующих процентилей с равной вероятностью, а method определяет способ их вычисления.

Примечание: statistics.quantiles() введено в Python 3.8.

Вы также можете использовать np.percentile() для определения любого процентиля выборки в вашем наборе данных. Например, вот как вы можете найти 5-й и 95-й процентили:

>>> y = np.array(x)
>>> np.percentile(y, 5)
-3.44
>>> np.percentile(y, 95)
34.919999999999995

percentile() принимает несколько аргументов. В качестве первого аргумента необходимо указать набор данных, а в качестве второго - процентильное значение. Набор данных может быть в виде числового массива, списка, кортежа или аналогичной структуры данных. Процентиль может быть числом от 0 до 100, как в примере выше, но также может быть и последовательностью чисел:

>>> np.percentile(y, [25, 50, 75])
array([ 0.1,  8. , 21. ])
>>> np.median(y)
8.0

Этот код вычисляет 25-й, 50-й и 75-й процентили одновременно. Если значение процентиля является последовательностью, то percentile() возвращает числовой массив с результатами. Первая инструкция возвращает массив квартилей. Вторая инструкция возвращает медиану, чтобы вы могли убедиться, что она равна 50-му процентилю, который равен 8.0.

Если вы хотите игнорировать значения nan, то используйте np.nanpercentile() вместо этого:

>>> y_with_nan = np.insert(y, 2, np.nan)
>>> y_with_nan
array([-5. , -1.1,  nan,  0.1,  2. ,  8. , 12.8, 21. , 25.8, 41. ])
>>> np.nanpercentile(y_with_nan, [25, 50, 75])
array([ 0.1,  8. , 21. ])

Вот как вы можете избежать значений nan.

NumPy также предлагает вам очень похожие функциональные возможности в quantile() и nanquantile(). Если вы используете их, то вам нужно будет указать значения квантилей в виде чисел от 0 до 1 вместо процентилей:

>>> np.quantile(y, 0.05)
-3.44
>>> np.quantile(y, 0.95)
34.919999999999995
>>> np.quantile(y, [0.25, 0.5, 0.75])
array([ 0.1,  8. , 21. ])
>>> np.nanquantile(y_with_nan, [0.25, 0.5, 0.75])
array([ 0.1,  8. , 21. ])

Результаты такие же, как и в предыдущих примерах, но здесь ваши аргументы находятся в диапазоне от 0 до 1. Другими словами, вы передали 0.05 вместо 5 и 0.95 вместо 95.

pd.Series объекты имеют метод .quantile():

>>> z, z_with_nan = pd.Series(y), pd.Series(y_with_nan)
>>> z.quantile(0.05)
-3.44
>>> z.quantile(0.95)
34.919999999999995
>>> z.quantile([0.25, 0.5, 0.75])
0.25     0.1
0.50     8.0
0.75    21.0
dtype: float64
>>> z_with_nan.quantile([0.25, 0.5, 0.75])
0.25     0.1
0.50     8.0
0.75    21.0
dtype: float64

.quantile() также необходимо указать значение квантиля в качестве аргумента. Это значение может быть числом от 0 до 1 или последовательностью чисел. В первом случае .quantile() возвращает скаляр. Во втором случае он возвращает новый Series, содержащий результаты.

Диапазоны

Диапазон данных - это разница между максимальным и минимальным элементом в наборе данных. Вы можете получить это с помощью функции np.ptp():

>>> np.ptp(y)
46.0
>>> np.ptp(z)
46.0
>>> np.ptp(y_with_nan)
nan
>>> np.ptp(z_with_nan)
46.0

Эта функция возвращает nan, если в вашем массиве NumPy есть значения nan. Если вы используете объект pandas Series, то он вернет число.

В качестве альтернативы вы можете использовать встроенные функции и методы Python, NumPy или pandas для вычисления максимумов и минимумов последовательностей:

• max() и min() из стандартной библиотеки Python
• amax() и amin() из NumPy
• nanmax() и nanmin() из NumPy в ignore nan значения
• .max() и .min() из NumPy
• .max() и .min() из pandas игнорировать nan значения по умолчанию

Вот несколько примеров того, как вы могли бы использовать эти процедуры:

>>> np.amax(y) - np.amin(y)
46.0
>>> np.nanmax(y_with_nan) - np.nanmin(y_with_nan)
46.0
>>> y.max() - y.min()
46.0
>>> z.max() - z.min()
46.0
>>> z_with_nan.max() - z_with_nan.min()
46.0

Вот как вы получаете диапазон данных.

Межквартильный диапазон - это разница между первым и третьим квартилями. Как только вы рассчитаете квартили, вы можете взять их разницу:

>>> quartiles = np.quantile(y, [0.25, 0.75])
>>> quartiles[1] - quartiles[0]
20.9
>>> quartiles = z.quantile([0.25, 0.75])
>>> quartiles[0.75] - quartiles[0.25]
20.9

Обратите внимание, что вы получаете доступ к значениям в объекте pandas Series с помощью меток 0.75 и 0.25.

Краткое изложение описательной статистики

SciPy и pandas предлагают полезные процедуры для быстрого получения описательной статистики с помощью одного вызова функции или метода. Вы можете использовать scipy.stats.describe() следующим образом:

>>> result = scipy.stats.describe(y, ddof=1, bias=False)
>>> result
DescribeResult(nobs=9, minmax=(-5.0, 41.0), mean=11.622222222222222, variance=228.75194444444446, skewness=0.9249043136685094, kurtosis=0.14770623629658886)

В качестве первого аргумента необходимо указать набор данных. Аргументом может быть массив NumPy, список, кортеж или аналогичная структура данных. Вы можете опустить ddof=1, поскольку это значение используется по умолчанию и имеет значение только при расчете дисперсии. Вы можете передать bias=False для принудительной коррекции асимметрии и эксцесса для статистической погрешности.

Примечание: Необязательный параметр nan_policy может принимать значения 'propagate' (по умолчанию), 'raise' ( ошибка), или 'omit'. Этот параметр позволяет вам управлять тем, что происходит при наличии значений nan.

describe() возвращает объект, содержащий следующую описательную статистику:

• nobs: количество наблюдений или элементов в вашем наборе данных
• minmax: кортеж с минимальными и максимальными значениями вашего набора данных
• mean: среднее значение вашего набора данных
• variance: дисперсия вашего набора данных
• skewness: асимметрия вашего набора данных
• kurtosis: эксцесс вашего набора данных

Вы можете получить доступ к определенным значениям с помощью точечной записи:

>>> result.nobs
9
>>> result.minmax[0]  # Min
-5.0
>>> result.minmax[1]  # Max
41.0
>>> result.mean
11.622222222222222
>>> result.variance
228.75194444444446
>>> result.skewness
0.9249043136685094
>>> result.kurtosis
0.14770623629658886

С помощью SciPy всего один вызов функции отделяет вас от получения сводки описательной статистики для вашего набора данных.

pandas обладает аналогичной, если не лучшей, функциональностью. Series объекты имеют метод .describe():

>>> result = z.describe()
>>> result
count     9.000000
mean     11.622222
std      15.124548
min      -5.000000
25%       0.100000
50%       8.000000
75%      21.000000
max      41.000000
dtype: float64

Он возвращает новый Series, содержащий следующее:

• count: количество элементов в вашем наборе данных
• mean: среднее значение вашего набора данных
• std: стандартное отклонение вашего набора данных
• min и max: минимальное и максимальное значения вашего набора данных
• 25%, 50%, и 75%: квартили вашего набора данных

Если вы хотите, чтобы результирующий объект Series содержал другие процентили, то вам следует указать значение необязательного параметра percentiles. Вы можете получить доступ к каждому элементу result с его меткой:

>>> result['mean']
11.622222222222222
>>> result['std']
15.12454774346805
>>> result['min']
-5.0
>>> result['max']
41.0
>>> result['25%']
0.1
>>> result['50%']
8.0
>>> result['75%']
21.0

Вот как вы можете получить описательную статистику объекта Series с помощью одного вызова метода с использованием pandas.

Показатели корреляции между парами данных

Вам часто приходится проверять взаимосвязь между соответствующими элементами двух переменных в наборе данных. Допустим, есть две переменные 𝑥 и 𝑦 с равным количеством элементов 𝑛. Пусть 𝑥₁ от 𝑥 𝑦соответствуют ₁ Из 𝑦, 𝑥 𝑥 𝑦 𝑦 ₂ ₂ от до С, и так далее. Затем вы можете сказать, что существует 𝑛 пар соответствующих элементов: (𝑥₁, 𝑦₁), (𝑥₂, 𝑦₂) и так далее.

Вы увидите следующие показатели корреляции между парами данных:

• Положительная корреляция существует, когда большие значения θ соответствуют большим значениям θ и наоборот.
• Отрицательная корреляция существует, когда большие значения θ соответствуют меньшим значениям θ и наоборот.
• Слабая корреляция или ее полное отсутствие существует, если нет такой очевидной взаимосвязи.

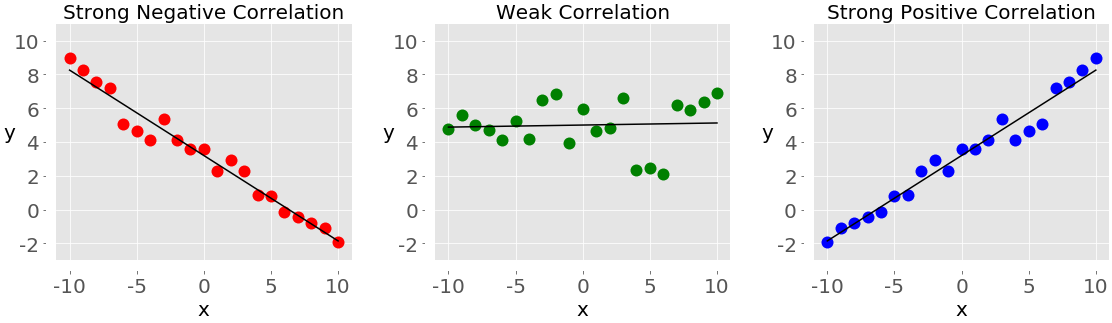
На следующем рисунке показаны примеры отрицательной, слабой и положительной корреляции:

График слева с красными точками показывает отрицательную корреляцию. График посередине с зелеными точками показывает слабую корреляцию. Наконец, график справа с синими точками показывает положительную корреляцию.

Примечание: Есть одна важная вещь, которую вы всегда должны иметь в виду при работе с корреляцией между парой переменных, и это то, что корреляция не является мерой или показатель причинно-следственной связи, но только ассоциации!

Двумя статистическими данными, которые измеряют корреляцию между наборами данных, являются ковариация и коэффициент корреляции. Давайте определим некоторые данные для работы с этими показателями. Вы создадите два списка на Python и будете использовать их для получения соответствующих массивов NumPy и pandas Series:

>>> x = list(range(-10, 11))
>>> y = [0, 2, 2, 2, 2, 3, 3, 6, 7, 4, 7, 6, 6, 9, 4, 5, 5, 10, 11, 12, 14]
>>> x_, y_ = np.array(x), np.array(y)
>>> x__, y__ = pd.Series(x_), pd.Series(y_)

Теперь, когда у вас есть две переменные, вы можете приступить к изучению взаимосвязи между ними.

Ковариация

Выборочная ковариация - это показатель, который количественно определяет силу и направление взаимосвязи между парой переменных:

• Если корреляция положительная, то и ковариация также положительна. Более сильная взаимосвязь соответствует более высокому значению ковариации.
• Если корреляция отрицательна, то ковариация также отрицательна. Более сильная взаимосвязь соответствует более низкому (или более высокому абсолютному) значению ковариации.
• Если корреляция слабая, то ковариация близка к нулю.

ковариации переменных 𝑥 и 𝑦 математически определяется как 𝑠ˣʸ = Σᵢ (𝑥ᵢ − означает(𝑥)) (𝑦ᵢ − значит(𝑦)) / (𝑛 − 1), где 𝑖 = 1, 2, ..., 𝑛, имею в виду(𝑥) является выборочной средней от 𝑥 и среднее(𝑦) является выборочное среднее из 𝑦. Из этого следует, что ковариации двух одинаковых переменных фактически разница: 𝑠ˣˣ = Σᵢ(𝑥ᵢ − значит(𝑥))2 / (𝑛 − 1) = (𝑠ˣ)2 и 𝑠ʸʸ = Σᵢ(𝑦ᵢ − значит(𝑦))2 / (𝑛 − 1) = (𝑠ʸ)2.

Вот как вы можете вычислить ковариацию в чистом Python:

>>> n = len(x)
>>> mean_x, mean_y = sum(x) / n, sum(y) / n
>>> cov_xy = (sum((x[k] - mean_x) * (y[k] - mean_y) for k in range(n))
...           / (n - 1))
>>> cov_xy
19.95

Сначала вам нужно найти среднее значение для x и y. Затем вы применяете математическую формулу для ковариации.

В NumPy есть функция cov(), которая возвращает ковариационную матрицу:

>>> cov_matrix = np.cov(x_, y_)
>>> cov_matrix
array([[38.5       , 19.95      ],
       [19.95      , 13.91428571]])

Обратите внимание, что cov() имеет необязательные параметры bias, значение которых по умолчанию равно False, и ddof, значение которых по умолчанию равно None. Их значения по умолчанию подходят для получения выборочной ковариационной матрицы. Верхний левый элемент ковариационной матрицы представляет собой ковариацию x и x или дисперсию x. Аналогично, нижний правый элемент представляет собой ковариацию y и y или дисперсию y. Вы можете проверить, верно ли это:

>>> x_.var(ddof=1)
38.5
>>> y_.var(ddof=1)
13.914285714285711

Как вы можете видеть, отклонения значений x и y равны cov_matrix[0, 0] и cov_matrix[1, 1] соответственно.

Два других элемента ковариационной матрицы равны и представляют фактическую ковариацию между x и y:

>>> cov_xy = cov_matrix[0, 1]
>>> cov_xy
19.95
>>> cov_xy = cov_matrix[1, 0]
>>> cov_xy
19.95

Вы получили то же значение ковариации с np.cov(), что и с чистым Python.

у панд Series есть метод .cov(), который вы можете использовать для вычисления ковариации:

>>> cov_xy = x__.cov(y__)
>>> cov_xy
19.95
>>> cov_xy = y__.cov(x__)
>>> cov_xy
19.95

Здесь вы вызываете .cov() для одного Series объекта и передаете другой объект в качестве первого аргумента.

Коэффициент корреляции

Коэффициент корреляции , или Коэффициент корреляции произведения Пирсона с моментом, обозначается символом 𝑟. Коэффициент - это еще один показатель корреляции между данными. Вы можете рассматривать его как стандартизированную ковариацию. Вот несколько важных фактов об этом:

• Значение 𝑟 > 0 указывает на положительную корреляцию.
• Значение 𝑟 < 0 указывает на отрицательную корреляцию.
• Значение r = 1 является максимально возможным значением θ. Это соответствует идеальной положительной линейной зависимости между переменными.
• Значение r = -1 является минимально возможным значением θ. Это соответствует идеальной отрицательной линейной зависимости между переменными.
• Значение r ≈ 0, или когда θ равно нулю, означает, что корреляция между переменными слабая.

математическая формула для коэффициента корреляции 𝑟 = 𝑠ˣʸ / (ˣ ʸ𝑠𝑠), где 𝑠𝑠и ˣ ʸ стандартные отклонения 𝑥 и 𝑦 соответственно. Если у вас есть средние значения (mean_x и mean_y) и стандартные отклонения (std_x, std_y) для наборов данных x и y, а также их ковариацию cov_xy, то вы можете рассчитать коэффициент корреляции с помощью чистого Python:

>>> var_x = sum((item - mean_x)**2 for item in x) / (n - 1)
>>> var_y = sum((item - mean_y)**2 for item in y) / (n - 1)
>>> std_x, std_y = var_x ** 0.5, var_y ** 0.5
>>> r = cov_xy / (std_x * std_y)
>>> r
0.861950005631606

У вас есть переменная r, которая представляет коэффициент корреляции.

scipy.stats имеет процедуру pearsonr(), которая вычисляет коэффициент корреляции и 𝑝-значение:

>>> r, p = scipy.stats.pearsonr(x_, y_)
>>> r
0.861950005631606
>>> p
5.122760847201171e-07

pearsonr() возвращает кортеж с двумя числами. Первое из них равно 𝑟, а второе - 𝑝-значение.

Аналогично случаю с ковариационной матрицей, вы можете применить np.corrcoef() с x_ и y_ в качестве аргументов и получить матрицу коэффициентов корреляции :

>>> corr_matrix = np.corrcoef(x_, y_)
>>> corr_matrix
array([[1.        , 0.86195001],
       [0.86195001, 1.        ]])

Верхний левый элемент - это коэффициент корреляции между x_ и x_. Нижний правый элемент - это коэффициент корреляции между y_ и y_. Их значения равны 1.0. Два других элемента равны и представляют фактический коэффициент корреляции между x_ и y_:

>>> r = corr_matrix[0, 1]
>>> r
0.8619500056316061
>>> r = corr_matrix[1, 0]
>>> r
0.861950005631606

Конечно, результат будет таким же, как и при использовании чистого Python и pearsonr().

Вы можете получить коэффициент корреляции с scipy.stats.linregress():

>>> scipy.stats.linregress(x_, y_)
LinregressResult(slope=0.5181818181818181, intercept=5.714285714285714, rvalue=0.861950005631606, pvalue=5.122760847201164e-07, stderr=0.06992387660074979)

linregress() принимает значения x_ и y_, выполняет линейную регрессию и возвращает результаты. slope и intercept определяют уравнение линии регрессии, в то время как rvalue - коэффициент корреляции. Чтобы получить доступ к конкретным значениям из результата linregress(), включая коэффициент корреляции, используйте точечное обозначение:

>>> result = scipy.stats.linregress(x_, y_)
>>> r = result.rvalue
>>> r
0.861950005631606

Вот как вы можете выполнить линейную регрессию и получить коэффициент корреляции.

у панд Series есть метод .corr() для расчета коэффициента корреляции:

>>> r = x__.corr(y__)
>>> r
0.8619500056316061
>>> r = y__.corr(x__)
>>> r
0.861950005631606

Вы должны вызвать .corr() для одного объекта Series и передать другой объект в качестве первого аргумента.

Работа с 2D-данными

Статистики часто работают с 2D-данными. Вот несколько примеров форматов 2D-данных:

• База данных таблицы
• CSV-файлы
• Электронные таблицы Excel, Calc и Google

NumPy и SciPy предоставляют комплексные средства для работы с 2D-данными. в pandas есть класс DataFrame, предназначенный специально для обработки 2D-помеченных данных.

Оси

Начните с создания двумерного массива NumPy:

>>> a = np.array([[1, 1, 1],
...               [2, 3, 1],
...               [4, 9, 2],
...               [8, 27, 4],
...               [16, 1, 1]])
>>> a
array([[ 1,  1,  1],
       [ 2,  3,  1],
       [ 4,  9,  2],
       [ 8, 27,  4],
       [16,  1,  1]])

Теперь у вас есть 2D-набор данных, который вы будете использовать в этом разделе. Вы можете применить к нему статистические функции и методы Python так же, как к 1D-данным:

>>> np.mean(a)
5.4
>>> a.mean()
5.4
>>> np.median(a)
2.0
>>> a.var(ddof=1)
53.40000000000001

Как вы можете видеть, вы получаете статистику (например, среднее значение, медиану или дисперсию) по всем данным в массиве a. Иногда вам нужно именно такое поведение, но в некоторых случаях вы захотите, чтобы эти величины были рассчитаны для каждой строки или столбца вашего двумерного массива.

Функции и методы, которые вы использовали до сих пор, имеют один необязательный параметр под названием axis,, который необходим для обработки двумерных данных. axis может принимать любое из следующих значений:

• axis=None используется для вычисления статистики по всем данным в массиве. Приведенные выше примеры работают следующим образом. Такое поведение часто используется в NumPy по умолчанию.
• axis=0 используется для вычисления статистики по всем строкам, то есть для каждого столбца массива. Такое поведение часто используется по умолчанию для статистических функций SciPy.
• axis=1 используется для вычисления статистики по всем столбцам, то есть для каждой строки массива.

Давайте посмотрим на axis=0 в действии с np.mean():

>>> np.mean(a, axis=0)
array([6.2, 8.2, 1.8])
>>> a.mean(axis=0)
array([6.2, 8.2, 1.8])

Два приведенных выше оператора возвращают новые массивы NumPy со средним значением для каждого столбца a. В этом примере среднее значение для первого столбца равно 6.2. Во втором столбце указано среднее значение 8.2, а в третьем - 1.8.

Если вы укажете значение от axis=1 до mean(), то получите результаты для каждой строки:

>>> np.mean(a, axis=1)
array([ 1.,  2.,  5., 13.,  6.])
>>> a.mean(axis=1)
array([ 1.,  2.,  5., 13.,  6.])

Как вы можете видеть, первая строка a имеет среднее значение 1.0, вторая 2.0 и так далее.

Примечание: Вы можете распространить эти правила на многомерные массивы, но это выходит за рамки данного руководства. Не стесняйтесь углубляться в эту тему самостоятельно!

Параметр axis работает таким же образом с другими функциями и методами NumPy:

>>> np.median(a, axis=0)
array([4., 3., 1.])
>>> np.median(a, axis=1)
array([1., 2., 4., 8., 1.])
>>> a.var(axis=0, ddof=1)
array([ 37.2, 121.2,   1.7])
>>> a.var(axis=1, ddof=1)
array([  0.,   1.,  13., 151.,  75.])

У вас есть медианы и примерные варианты для всех столбцов (axis=0) и строк (axis=1) массива a.

Это очень похоже на работу со статистическими функциями SciPy. Но помните, что в этом случае значение по умолчанию для axis равно 0:

>>> scipy.stats.gmean(a)  # Default: axis=0
array([4.        , 3.73719282, 1.51571657])
>>> scipy.stats.gmean(a, axis=0)
array([4.        , 3.73719282, 1.51571657])

Если вы опустите axis или укажете axis=0, то получите результат по всем строкам, то есть по каждому столбцу. Например, первый столбец a имеет среднее геометрическое значение 4.0 и так далее.

Если вы укажете axis=1, то получите вычисления по всем столбцам, то есть для каждой строки:

>>> scipy.stats.gmean(a, axis=1)
array([1.        , 1.81712059, 4.16016765, 9.52440631, 2.5198421 ])

В этом примере среднее геометрическое значение первой строки a равно 1.0. Для второго ряда это примерно 1.82 и так далее.

Если вам нужна статистика по всему набору данных, то вы должны предоставить axis=None:

>>> scipy.stats.gmean(a, axis=None)
2.829705017016332

Среднее геометрическое значение всех элементов в массиве a приблизительно равно 2.83.

Вы можете получить сводку статистики Python с помощью одного вызова функции для 2D-данных с помощью scipy.stats.describe(). Это работает аналогично 1D-массивам, но вы должны быть осторожны с параметром axis:

>>> scipy.stats.describe(a, axis=None, ddof=1, bias=False)
DescribeResult(nobs=15, minmax=(1, 27), mean=5.4, variance=53.40000000000001, skewness=2.264965290423389, kurtosis=5.212690982795767)
>>> scipy.stats.describe(a, ddof=1, bias=False)  # Default: axis=0
DescribeResult(nobs=5, minmax=(array([1, 1, 1]), array([16, 27,  4])), mean=array([6.2, 8.2, 1.8]), variance=array([ 37.2, 121.2,   1.7]), skewness=array([1.32531471, 1.79809454, 1.71439233]), kurtosis=array([1.30376344, 3.14969121, 2.66435986]))
>>> scipy.stats.describe(a, axis=1, ddof=1, bias=False)
DescribeResult(nobs=3, minmax=(array([1, 1, 2, 4, 1]), array([ 1,  3,  9, 27, 16])), mean=array([ 1.,  2.,  5., 13.,  6.]), variance=array([  0.,   1.,  13., 151.,  75.]), skewness=array([0.        , 0.        , 1.15206964, 1.52787436, 1.73205081]), kurtosis=array([-3. , -1.5, -1.5, -1.5, -1.5]))

Когда вы вводите axis=None, вы получаете сводку по всем данным. Большинство результатов являются скалярными. Если вы задаете axis=0 или опускаете ее, то возвращаемое значение будет сводкой по каждому столбцу. Таким образом, большинство результатов представляют собой массивы с таким же количеством элементов, как и количество столбцов. Если вы задаете axis=1, то describe() возвращает сводку по всем строкам.

Вы можете получить конкретное значение из сводки с точечным обозначением:

>>> result = scipy.stats.describe(a, axis=1, ddof=1, bias=False)
>>> result.mean
array([ 1.,  2.,  5., 13.,  6.])

Вот как вы можете увидеть сводную статистику для двумерного массива с помощью одного вызова функции.

Фреймы данных

Класс DataFrame является одним из основных типов данных pandas. С ним очень удобно работать, поскольку у него есть метки для строк и столбцов. Используйте массив a и создайте DataFrame:

>>> row_names = ['first', 'second', 'third', 'fourth', 'fifth']
>>> col_names = ['A', 'B', 'C']
>>> df = pd.DataFrame(a, index=row_names, columns=col_names)
>>> df
         A   B  C
first    1   1  1
second   2   3  1
third    4   9  2
fourth   8  27  4
fifth   16   1  1

На практике названия столбцов имеют значение и должны быть описательными. Названия строк иногда автоматически задаются как 0, 1, и так далее. Вы можете указать их явно с помощью параметра index, хотя вы можете опустить index, если хотите.

DataFrame методы очень похожи на методы Series, хотя их поведение отличается. Если вы вызываете статистические методы Python без аргументов, то DataFrame вернет результаты для каждого столбца:

>>> df.mean()
A    6.2
B    8.2
C    1.8
dtype: float64
>>> df.var()
A     37.2
B    121.2
C      1.7
dtype: float64

Вы получите новый Series, содержащий результаты. В этом случае Series содержит среднее значение и дисперсию для каждого столбца. Если вам нужны результаты для каждой строки, то просто укажите параметр axis=1:

>>> df.mean(axis=1)
first      1.0
second     2.0
third      5.0
fourth    13.0
fifth      6.0
dtype: float64
>>> df.var(axis=1)
first       0.0
second      1.0
third      13.0
fourth    151.0
fifth      75.0
dtype: float64

В результате получится Series с требуемым количеством для каждой строки. Надписи 'first', 'second', и так далее относятся к разным строкам.

Вы можете выделить каждый столбец из DataFrame следующим образом:

>>> df['A']
first      1
second     2
third      4
fourth     8
fifth     16
Name: A, dtype: int64

Теперь у вас есть столбец 'A' в виде объекта Series и вы можете применить соответствующие методы:

>>> df['A'].mean()
6.2
>>> df['A'].var()
37.20000000000001

Вот как вы можете получить статистику для одного столбца.

Иногда вы можете захотеть использовать DataFrame в качестве числового массива и применить к нему какую-либо функцию. Можно получить все данные из DataFrame с помощью .values или .to_numpy():

>>> df.values
array([[ 1,  1,  1],
       [ 2,  3,  1],
       [ 4,  9,  2],
       [ 8, 27,  4],
       [16,  1,  1]])
>>> df.to_numpy()
array([[ 1,  1,  1],
       [ 2,  3,  1],
       [ 4,  9,  2],
       [ 8, 27,  4],
       [16,  1,  1]])

df.values и df.to_numpy() дает вам массив NumPy со всеми элементами из DataFrame без меток строк и столбцов. Обратите внимание, что df.to_numpy() является более гибким, поскольку вы можете указать тип данных элементов и то, хотите ли вы использовать существующие данные или скопировать их.

Нравится Series, DataFrame объекты имеют метод .describe() который возвращает другой DataFrame с сводная статистика по всем столбцам:

>>> df.describe()
              A          B        C
count   5.00000   5.000000  5.00000
mean    6.20000   8.200000  1.80000
std     6.09918  11.009087  1.30384
min     1.00000   1.000000  1.00000
25%     2.00000   1.000000  1.00000
50%     4.00000   3.000000  1.00000
75%     8.00000   9.000000  2.00000
max    16.00000  27.000000  4.00000

В сводке содержатся следующие результаты:

• count: количество элементов в каждом столбце
• mean: среднее значение по каждому столбцу
• std: стандартное отклонение
• min и max: минимальное и максимальное значения
• 25%, 50%, и 75%: процентили

Если вы хотите, чтобы результирующий объект DataFrame содержал другие процентили, то вам следует указать значение необязательного параметра percentiles.

Вы можете получить доступ к каждому элементу сводки следующим образом:

>>> df.describe().at['mean', 'A']
6.2
>>> df.describe().at['50%', 'B']
3.0

Вот как вы можете получить описательную статистику Python в одном Series объекте с помощью одного вызова метода pandas.

Визуализация данных

Помимо вычисления числовых величин, таких как среднее значение, медиана или дисперсия, вы можете использовать визуальные методы для представления, описания и обобщения данных. В этом разделе вы узнаете, как представить ваши данные визуально, используя следующие графики:

• Прямоугольные графики
• Гистограммы
• Круговые диаграммы
• Столбчатые диаграммы
• X-Y графики
• Тепловые карты

matplotlib.pyplot это очень удобная и широко используемая библиотека, хотя это не единственная библиотека Python, доступная для этой цели. Вы можете импортировать ее следующим образом:

>>> import matplotlib.pyplot as plt
>>> plt.style.use('ggplot')

Теперь matplotlib.pyplot импортирован и готов к использованию. Вторая инструкция задает стиль для ваших графиков, выбирая цвета, ширину линий и другие стилистические элементы. Вы можете не указывать их, если вас устраивают настройки стиля по умолчанию.

Примечание: В этом разделе основное внимание уделяется представлению данных и стилистические настройки сведены к минимуму. Вы увидите ссылки на официальную документацию по используемым процедурам из matplotlib.pyplot, так что вы можете изучить варианты, которых здесь нет.

Вы будете использовать псевдослучайные числа для получения данных для работы. Вам не нужны знания о случайных числах, чтобы понять этот раздел. Вам просто нужно несколько произвольных чисел, и генераторы псевдослучайных чисел - удобный инструмент для их получения. Модуль np.random генерирует массивы псевдослучайных чисел:

• Нормально распределенные числа генерируются с помощью np.random.randn().
• Равномерно распределенные целые числа генерируются с помощью np.random.randint().

В NumPy 1.17 появился еще один модуль для генерации псевдослучайных чисел. Чтобы узнать больше об этом, ознакомьтесь с официальной документацией .

Прямоугольные графики

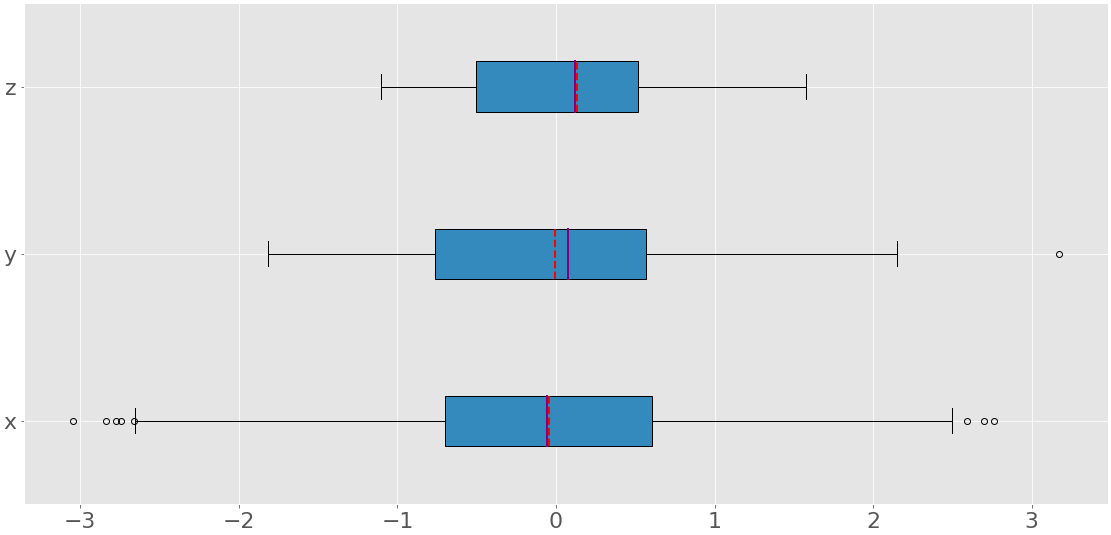
Прямоугольный график является отличным инструментом для визуального представления описательной статистики данного набора данных. Он может отображать диапазон, межквартильный интервал, медиану, режим, выбросы и все квартили. Сначала создайте некоторые данные для представления в виде прямоугольного графика:

>>> np.random.seed(seed=0)
>>> x = np.random.randn(1000)
>>> y = np.random.randn(100)
>>> z = np.random.randn(10)

Первый оператор задает начальное значение генератора случайных чисел NumPy с помощью seed(),, чтобы вы могли получать одни и те же результаты при каждом запуске кода. Вам не обязательно устанавливать начальное значение, но если вы не укажете это значение, то каждый раз будете получать разные результаты.

Другие инструкции генерируют три числовых массива с нормально распределенными псевдослучайными числами. x относится к массиву из 1000 элементов, y содержит 100 элементов, а z содержит 10 элементов. Теперь, когда у вас есть данные для работы, вы можете применить .boxplot() чтобы получить прямоугольный график:

fig, ax = plt.subplots()
ax.boxplot((x, y, z), vert=False, showmeans=True, meanline=True,
           labels=('x', 'y', 'z'), patch_artist=True,
           medianprops={'linewidth': 2, 'color': 'purple'},
           meanprops={'linewidth': 2, 'color': 'red'})
plt.show()

Параметры .boxplot() определяют следующее:

• x это ваши данные.
• vert устанавливает горизонтальную ориентацию графика при False. Ориентация по умолчанию - вертикальная.
• showmeans показывает среднее значение ваших данных, когда True.
• meanline представляет среднее значение в виде линии, когда True. По умолчанию используется точка.
• labels: метки ваших данных.
• patch_artist определяет, как рисовать график.
• medianprops обозначает свойства линии, представляющей собой медиану.
• meanprops указывает свойства линии или точки, представляющих среднее значение.

Существуют и другие параметры, но их анализ выходит за рамки данного руководства.

Приведенный выше код создает изображение, подобное этому:

Вы можете увидеть три прямоугольных графика. Каждый из них соответствует отдельному набору данных (x, y, или z) и отображает следующее:

• Среднее значение обозначено красной пунктирной линией.
• Медиана - это фиолетовая линия.
• Первый квартиль - это левый край синего прямоугольника.
• Третий квартиль - это правый край синего прямоугольника.
• Межквартильный диапазон - это длина синего прямоугольника.
• Диапазон содержит все данные слева направо.
• Выбросы - это точки слева и справа.

Прямоугольный график может отображать так много информации на одном рисунке!

Гистограммы

Гистограммы особенно полезны, когда в наборе данных содержится большое количество уникальных значений. Гистограмма делит значения из отсортированного набора данных на интервалы, которые также называются ячейки. Часто все ячейки имеют одинаковую ширину, хотя это необязательно. Значения нижней и верхней границ ячейки называются краями ячейки.

Частота - это единственное значение, соответствующее каждой ячейке. Это количество элементов набора данных со значениями между краями ячейки. По общему правилу, все ячейки, кроме самой правой, являются полуоткрытыми. Они включают значения, равные нижним границам, но исключают значения, равные верхним границам. Крайняя правая ячейка закрыта, поскольку она включает обе границы. Если вы разделите набор данных с ребрами ячейки 0, 5, 10 и 15, то получится три ячейки:

1. Первая и крайняя левая ячейка содержит значения, которые больше или равны 0 и меньше 5.
2. Вторая ячейка содержит значения больше или равные 5 и меньше 10.
3. Третья и крайняя справа ячейка содержит значения больше или равные 10 и меньше или равные 15.

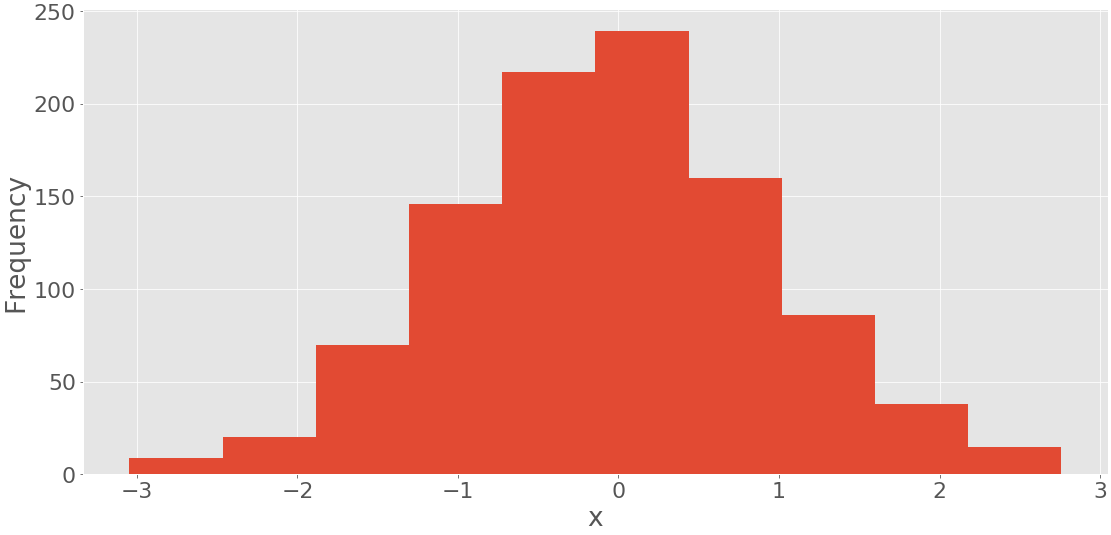
Функция np.histogram() - это удобный способ получения данных для гистограмм:

>>> hist, bin_edges = np.histogram(x, bins=10)
>>> hist
array([  9,  20,  70, 146, 217, 239, 160,  86,  38,  15])
>>> bin_edges
array([-3.04614305, -2.46559324, -1.88504342, -1.3044936 , -0.72394379,
       -0.14339397,  0.43715585,  1.01770566,  1.59825548,  2.1788053 ,
        2.75935511])

Он берет массив с вашими данными и количеством (или ребрами) ячеек и возвращает два числовых массива:

1. hist содержит частоту или количество элементов, соответствующих каждой ячейке.
2. bin_edges содержит ребра или границы ячейки.

Что вычисляет histogram(), .hist() можно показать графически:

fig, ax = plt.subplots()
ax.hist(x, bin_edges, cumulative=False)
ax.set_xlabel('x')
ax.set_ylabel('Frequency')
plt.show()

Первый аргумент .hist() - это последовательность с вашими данными. Второй аргумент определяет границы ячеек. Третий отключает возможность создания гистограммы с кумулятивными значениями. Приведенный выше код выдает цифру, подобную этой:

Вы можете увидеть границы ячейки на горизонтальной оси и частоты на вертикальной оси.

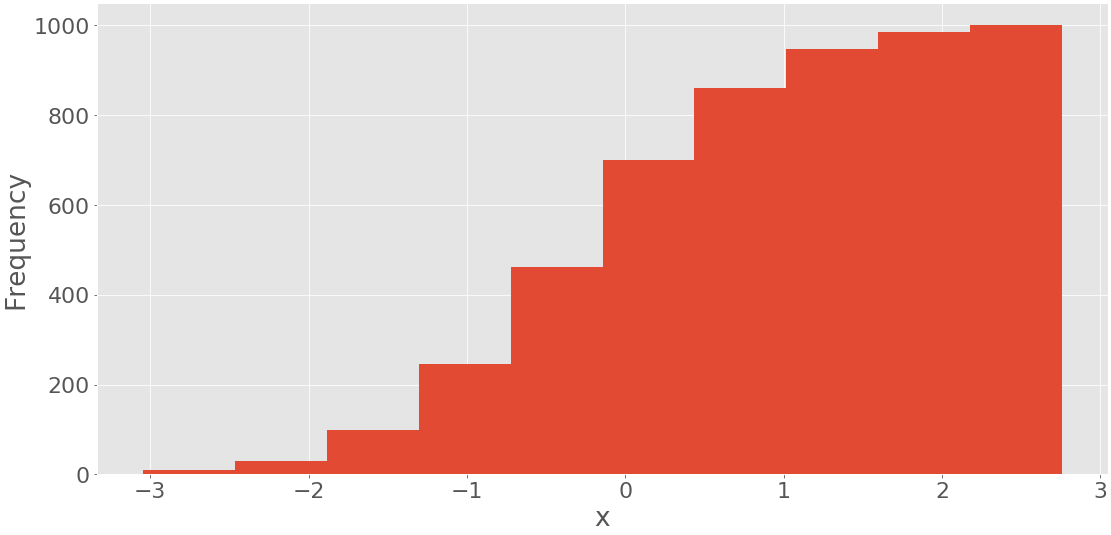
Можно получить гистограмму с суммарным количеством элементов, если указать аргумент cumulative=True для .hist():

fig, ax = plt.subplots()
ax.hist(x, bin_edges, cumulative=True)
ax.set_xlabel('x')
ax.set_ylabel('Frequency')
plt.show()

Этот код выдает следующую цифру:

Отображается гистограмма с суммарными значениями. Частота первого и крайнего левого столбцов - это количество элементов в этом столбце. Частота второго столбца - это сумма чисел элементов в первом и втором столбцах. Остальные ячейки следуют той же схеме. Наконец, частота последней и самой правой ячейки равна общему количеству элементов в наборе данных (в данном случае 1000). Вы также можете напрямую нарисовать гистограмму с помощью pd.Series.hist() используя matplotlib в фоновом режиме.

Круговые диаграммы

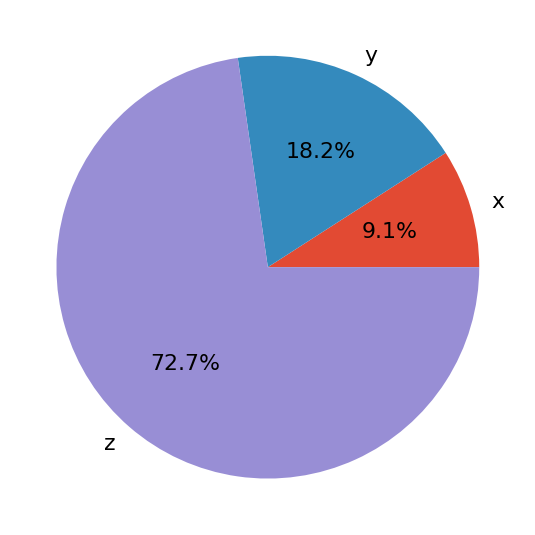
Круговые диаграммы представляют данные с небольшим количеством меток и заданными относительными частотами. Они хорошо работают даже с метками, которые невозможно упорядочить (например, с номинальными данными). Круговая диаграмма представляет собой круг, разделенный на несколько срезов. Каждый срез соответствует отдельной метке из набора данных и имеет площадь, пропорциональную относительной частоте, связанной с этой меткой.

Давайте определим данные, связанные с тремя метками:

>>> x, y, z = 128, 256, 1024

Теперь создайте круговую диаграмму с .pie():

fig, ax = plt.subplots()
ax.pie((x, y, z), labels=('x', 'y', 'z'), autopct='%1.1f%%')
plt.show()

Первый аргумент .pie() - это ваши данные, а второй - последовательность соответствующих меток. autopct определяет формат относительных частот, показанных на рисунке. У вас получится цифра, которая выглядит примерно так:

Круговая диаграмма показывает x как наименьшую часть круга, y как следующую по величине, а затем z как наибольшую часть. Проценты обозначают относительный размер каждого значения по сравнению с их суммой.

Столбчатые диаграммы

Столбчатые диаграммы также иллюстрируют данные, соответствующие заданным меткам или дискретным числовым значениям. Они могут отображать пары данных из двух наборов данных. Элементами одного набора являются меток, в то время как соответствующими элементами другого набора являются их частоты. При желании они также могут отображать ошибки, связанные с частотами.

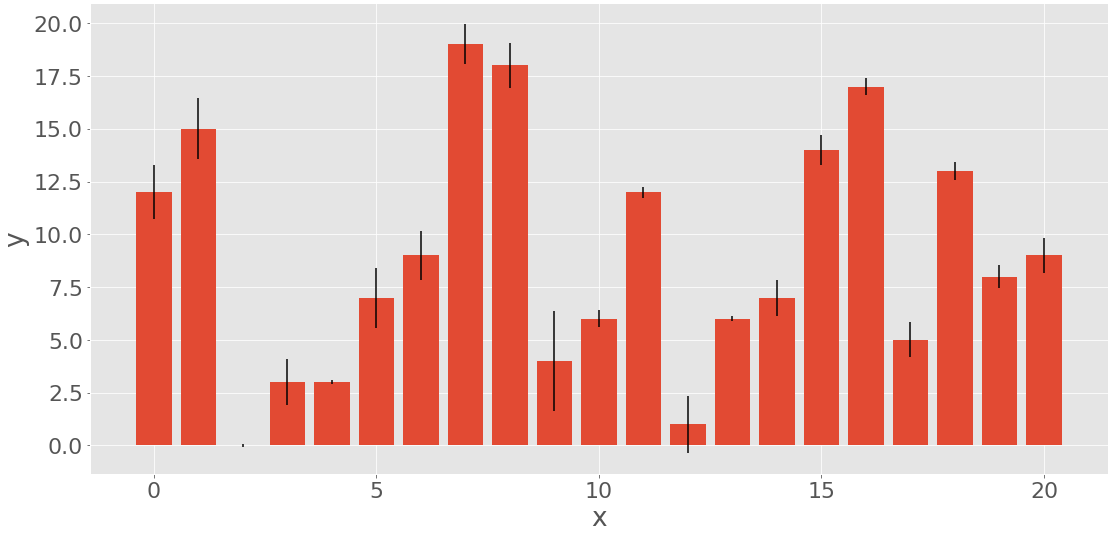
На столбчатой диаграмме показаны параллельные прямоугольники, называемые столбцами. Каждый столбец соответствует отдельной метке и имеет высоту, пропорциональную частоте или относительной частоте ее метки. Давайте сгенерируем три набора данных, каждый из которых содержит 21 элемент:

>>> x = np.arange(21)
>>> y = np.random.randint(21, size=21)
>>> err = np.random.randn(21)

Вы используете np.arange(), чтобы получить x, или массив последовательных целых чисел от 0 до 20. Вы будете использовать это для представления меток. y - это массив равномерно распределенных случайных целых чисел, также между 0 и 20. Этот массив будет представлять частоты. err содержит нормально распределенные числа с плавающей запятой, которые являются ошибками. Эти значения необязательны.

Вы можете создать столбчатую диаграмму с помощью .bar() если вам нужны вертикальные столбцы, или .barh() если вам нужны горизонтальные столбцы:

fig, ax = plt.subplots())
ax.bar(x, y, yerr=err)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()

Этот код должен выдавать следующую цифру:

Высота красных полос соответствует частотам y, в то время как длина черных линий показывает погрешности err. Если вы не хотите включать ошибки, то опустите параметр yerr из .bar().

Графики X-Y

График x-y или точечный график представляет пары данных из двух наборов данных. По горизонтальной оси x отложены значения из набора x, а по вертикальной оси y - соответствующие значения из набора y. При желании вы можете включить линию регрессии и коэффициент корреляции. Давайте сгенерируем два набора данных и выполним линейную регрессию с помощью scipy.stats.linregress():

>>> x = np.arange(21)
>>> y = 5 + 2 * x + 2 * np.random.randn(21)
>>> slope, intercept, r, *__ = scipy.stats.linregress(x, y)
>>> line = f'Regression line: y={intercept:.2f}+{slope:.2f}x, r={r:.2f}'

Набор данных x снова представляет собой массив с целыми числами от 0 до 20. y вычисляется как линейная функция от x, искаженная некоторым случайным шумом.

linregress возвращает несколько значений. Вам понадобятся slope и intercept линии регрессии, а также коэффициент корреляции r. Затем вы можете применить .plot() чтобы получить график x-y:

fig, ax = plt.subplots()
ax.plot(x, y, linewidth=0, marker='s', label='Data points')
ax.plot(x, intercept + slope * x, label=line)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(facecolor='white')
plt.show()

Результатом выполнения приведенного выше кода является следующая цифра:

Вы можете видеть точки данных (пары x-y) в виде красных квадратов, а также синюю линию регрессии.

Тепловые карты

Тепловая карта может быть использована для визуального отображения матрицы. Цвета представляют числа или элементы матрицы. Тепловые карты особенно полезны для иллюстрации ковариационной и корреляционной матриц. Вы можете создать тепловую карту для ковариационной матрицы с помощью .imshow():

matrix = np.cov(x, y).round(decimals=2)
fig, ax = plt.subplots()
ax.imshow(matrix)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1), ticklabels=('x', 'y'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('x', 'y'))
ax.set_ylim(1.5, -0.5)
for i in range(2):
    for j in range(2):
        ax.text(j, i, matrix[i, j], ha='center', va='center', color='w')
plt.show()

Здесь тепловая карта содержит метки 'x' и 'y', а также числа из ковариационной матрицы. У вас получится примерно такая цифра:

Желтое поле представляет самый большой элемент из матрицы 130.34, в то время как фиолетовое поле соответствует самому маленькому элементу 38.5. Синие квадраты между ними связаны со значением 69.9.

Вы можете получить тепловую карту для матрицы коэффициентов корреляции, следуя той же логике:

matrix = np.corrcoef(x, y).round(decimals=2)
fig, ax = plt.subplots()
ax.imshow(matrix)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1), ticklabels=('x', 'y'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('x', 'y'))
ax.set_ylim(1.5, -0.5)
for i in range(2):
    for j in range(2):
        ax.text(j, i, matrix[i, j], ha='center', va='center', color='w')
plt.show()

Результат представлен на рисунке ниже:

Желтый цвет обозначает значение 1.0, а фиолетовый показывает 0.99.

Заключение

Теперь вы знаете величины, которые описывают и обобщают наборы данных, и как их вычислять в Python. Можно получить описательную статистику с помощью чистого кода на Python, но это редко бывает необходимо. Обычно вы используете некоторые из библиотек, созданных специально для этой цели:

• Используйте Python statistics для наиболее важных статистических функций Python.
• Используйте NumPy для эффективной обработки массивов.
• Используйте SciPy для получения дополнительных статистических процедур Python для массивов NumPy.
• Используйте pandas для работы с помеченными наборами данных.
• Используйте Matplotlib для визуализации данных с помощью графиков, диаграмм и гистограмм.

Back to Top