Практическое машинное обучение с Python и Keras
Оглавление
- Что такое машинное обучение, и почему оно нас волнует?
- Сверхконтролируемое машинное обучение
- Понимание искусственных нейронных сетей
- Использование библиотеки Keras для обучения простой нейронной сети, распознающей рукописные цифры
- Запуск iPython Notebook локально
- Запуск из минимального дистрибутива Python
- Набор данных MNIST
- Цель
- Набор данных
- Чтение меток
- Чтение изображений
- Кодирование меток изображений с помощью одноточечного кодирования
- Обучение нейронной сети с помощью Keras
- Инспектирование результатов
- Понимание выхода активационного слоя softmax
- Чтение выхода активационного слоя softmax для нашей цифры
- Просмотр матрицы смешения
- Заключение
- Упражнение для дома
Что такое машинное обучение, и почему оно нас волнует?
Машинное обучение - это область искусственного интеллекта, которая использует статистические методы, чтобы дать компьютерным системам возможность "учиться" (например, постепенно улучшать производительность при выполнении конкретной задачи) на основе данных, без явного программирования. Вспомните, насколько эффективно (или неэффективно) Gmail обнаруживает спам в электронных письмах, или насколько качественным стало преобразование текста в речь с появлением Siri, Alexa и Google Home.
Некоторые из задач, которые можно решить с помощью внедрения машинного обучения, включают:
- Обнаружение аномалий и мошенничества: Выявление необычных закономерностей в кредитных картах и банковских транзакциях.
- Прогнозирование: Прогнозирование будущих цен на акции, обменных курсов, а теперь и криптовалют.
- Распознавание изображений: Идентификация объектов и лиц на изображениях.
Машинное обучение - это огромная область, и сегодня мы будем работать над анализом лишь небольшой ее части.
Supervised Machine Learning
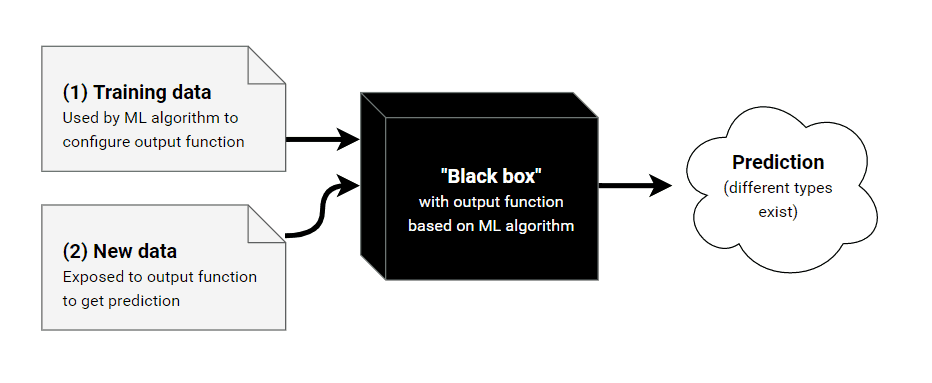
Supervised learning - это одна из подобластей машинного обучения. Идея контролируемого обучения заключается в том, что сначала вы учите систему понимать ваши прошлые данные, предоставляя множество примеров для конкретной проблемы и желаемого результата. Затем, когда система "обучена", вы можете показать ей новые входные данные, чтобы предсказать выходные данные.
Как построить детектор спама по электронной почте? Одним из способов является интуиция - ручное определение правил, которые имеют смысл: например, "содержит слово "деньги"" или "содержит слово "Western Union"". Хотя иногда системы, основанные на правилах, созданные вручную, могут работать, в других случаях становится трудно создавать или определять шаблоны и правила, основываясь только на человеческой интуиции. Используя метод контролируемого обучения, мы можем обучить системы автоматически определять основные правила и закономерности на основе большого количества прошлых данных о спаме. После того, как наш детектор спама обучен, мы можем скормить ему новое письмо, чтобы он мог предсказать, насколько вероятно, что письмо является спамом
Ранее я упоминал, что для прогнозирования результатов можно использовать контролируемое обучение. Существует два основных вида задач контролируемого обучения: регрессия и классификация.
- В задачах регрессии мы пытаемся предсказать непрерывный результат. Например, предсказать цену (реальную стоимость) дома при заданном его размере.
- В задачах классификации мы пытаемся предсказать дискретное число категориальных меток. Например, предсказать, является ли письмо спамом или нет, учитывая количество слов в нем.
Нельзя говорить о контролируемом машинном обучении, не говоря о моделях контролируемого обучения - это все равно, что говорить о программировании, не упоминая языки программирования или структуры данных. На самом деле, модели обучения - это структуры, которые "обучаются", и их веса или структура меняются по мере того, как они формируют и понимают то, что мы пытаемся предсказать. Существует множество моделей контролируемого обучения, некоторые из них я использовал лично:
- Случайный лес
- Naive Bayes
- Логистическая регрессия
- K Ближайшие соседи
Сегодня мы будем использовать искусственные нейронные сети (ИНС) в качестве выбранной нами модели.
Понимание искусственных нейронных сетей
Анны названы так потому, что их внутренняя структура призвана имитировать человеческий мозг. Человеческий мозг состоит из нейронов и синапсов, которые соединяют эти нейроны друг с другом, и когда эти нейроны стимулируются, они "активируют" другие нейроны в нашем мозге посредством электричества.
В мире ИНС каждый нейрон "активируется", сначала вычисляя взвешенную сумму своих входящих входов (других нейронов из предыдущего слоя), а затем прогоняя результат через функцию активации. Когда нейрон активирован, он, в свою очередь, активирует другие нейроны, которые выполняют аналогичные вычисления, вызывая цепную реакцию между всеми нейронами всех слоев.
Стоит отметить, что, хотя ИНС вдохновлены биологическими нейронами, они ни в коей мере не сопоставимы.
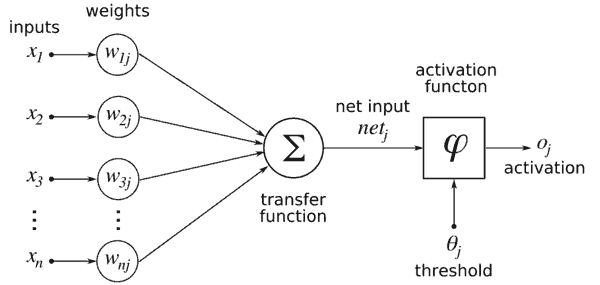
- На диаграмме выше описан весь процесс активации, через который проходит каждый нейрон. Давайте рассмотрим его слева направо.
- Считываются все входы (числовые значения) от входящих нейронов. Входящие входы обозначаются как x1...xn
- Каждый вход умножается на вес, связанный с этим соединением. Веса, связанные с соединениями здесь обозначаются как W1j...Wnj.
- Все взвешенные входы суммируются и передаются в функцию активации. Функция активации считывает один суммированный взвешенный вход и преобразует его в новое числовое значение.K Ближайшие соседи
- Наконец, числовое значение, возвращенное функцией активации, будет входом другого нейрона в другом слое.
Слои нейронной сети
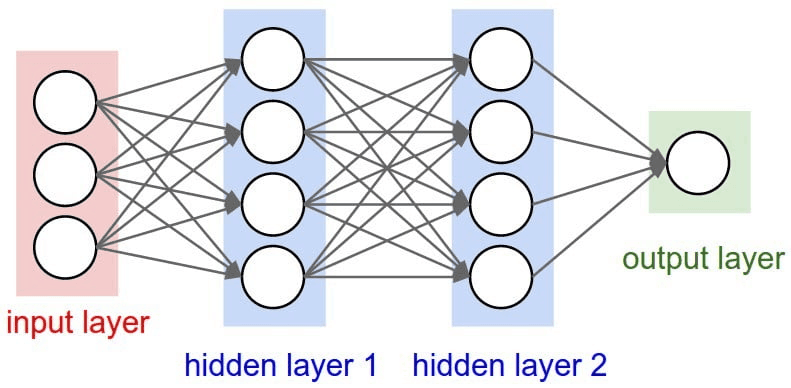
Нейроны в нейронной сети расположены по слоям. Слои - это способ придать структуру нейронной сети, каждый слой содержит 1 или более нейронов. Нейронная сеть обычно имеет 3 или более слоев. Есть 2 специальных слоя, которые всегда определены, это входной и выходной слои.
- Входной слой используется как точка входа в нашу нейронную сеть. В программировании это можно сравнить с аргументами, которые мы задаем функции.
- Выходной слой используется как результат нашей нейросети. В программировании считайте, что это возвращаемое значение функции.
Слои между ними называются "скрытыми слоями", и именно в них происходит большая часть вычислений. Все слои в ИНС кодируются как векторы признаков.
Выбор количества скрытых слоев и нейронов
Не всегда существует золотое правило выбора количества слоев и их размера (или количества нейронов). Как правило, нужно стараться иметь хотя бы 1 скрытый слой и подстраивать его размер, чтобы увидеть, что работает лучше всего.
Использование библиотеки Keras для обучения простой нейронной сети, распознающей рукописные цифры
Для нас, программистов Python, нет необходимости изобретать колесо. Такие библиотеки, как Tensorflow, Torch, Theano и Keras уже определяют основные структуры данных нейронной сети, оставляя нам ответственность за описание структуры нейронной сети в декларативной форме.
Keras предоставляет нам несколько степеней свободы: количество слоев, количество нейронов в каждом слое, тип слоя и функция активации. На практике их гораздо больше, но давайте будем упрощать. Как упоминалось выше, есть два специальных слоя, которые должны быть определены в зависимости от вашей проблемной области: размер входного слоя и размер выходного слоя. Все остальные "скрытые слои" могут быть использованы для обучения сложным нелинейным абстракциям проблемы.
Сегодня мы будем использовать Python и библиотеку Keras для предсказания рукописных цифр из набора данных MNIST. Есть три варианта следования: использовать отредактированный Jupyter Notebook, размещенный на github-репозитории Kite, запустить блокнот локально или запустить код из минимальной установки python на вашей машине.
Запуск iPython Notebook локально
Если вы хотите загрузить этот блокнот Jupyter Notebook локально вместо того, чтобы следовать за связанным рендеринговым блокнотом, вот как вы можете это настроить:
Требования:
- Операционная система Linux или Mac
- Conda 4.3.27 или более поздняя версия
- Git 2.13.0 или более поздней версии
- wget 1.16.3 или более поздняя версия
В терминале перейдите в выбранный вами каталог и выполните:
# Clone the repository
git clone https://github.com/kiteco/kite-python-blog-post-code.git
cd kite-python-blog-post-code/Practical\ Machine\ Learning\ with\ Python\ and\ Keras/
# Use Conda to setup and activate the Python environment with the correct dependencies
conda env create -f environment.yml
source activate kite-blog-post
Запуск с минимального дистрибутива Python
Для запуска из чистой установки Python (все, что после 3.5, должно работать), установите необходимые модули с помощью pip, затем запустите код как напечатан, исключая строки, отмеченные %, которые используются для среды iPython.
Настоятельно рекомендуется, но не обязательно, запускать код примера в виртуальной среде. Для получения дополнительной помощи см. https://packaging.python.org/guides/installing-using-pip-and-virtualenv/
# Set up and Activate a Virtual Environment under Python3
$ pip3 install virtualenv
$ python3 -m virtualenv venv
$ source venv/bin/activate
# Install Modules with pip (not pip3)
(venv) $ pip install matplotlib
(venv) $ pip install sklearn
(venv) $ pip install tensorflow
Хорошо! Если эти модули установились успешно, теперь вы можете запускать весь код в этом проекте.
В [1]:
import numpy as np
import matplotlib.pyplot as plt
import gzip
from typing import List
from sklearn.preprocessing import OneHotEncoder
import tensorflow.keras as keras
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import itertools
%matplotlib inline
Набор данных MNIST
<<<Набор данных MNIST - это большая база данных рукописных цифр, которая используется в качестве эталона и введения в системы машинного обучения и обработки изображений. Нам нравится MNIST, потому что набор данных очень чистый, и это позволяет нам сосредоточиться на реальном обучении и оценке сети. Помните: чистый набор данных - это роскошь в мире ML! Так что давайте наслаждаться и праздновать чистоту MNIST, пока это возможно 🙂
Цель
Получив набор данных из 60 000 изображений рукописных цифр (представленных 28×28 пикселями, каждый из которых содержит значение 0 - 255 в градациях серого), обучите систему классифицировать каждое изображение с соответствующей меткой (цифрой, которая отображается).
Набор данных
Набор данных состоит из обучающего и тестового наборов, но для простоты мы будем использовать только обучающий набор. Ниже мы можем загрузить обучающий набор данных
В [2]:
%%bash
rm -Rf train-images-idx3-ubyte.gz
rm -Rf train-labels-idx1-ubyte.gz
wget -q http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
wget -q http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Чтение меток
Существует 10 возможных рукописных цифр: (0-9), поэтому каждая метка должна быть числом от 0 до 9. Загруженный нами файл train-labels-idx1-ubyte.gz кодирует метки следующим образом:
Файл меток тренировочного набора (train-labels-idx1-ubyte):
| [offset] | [type] | [value] | [description] |
| 0000 | 32 bit integer | 0x00000801(2049) | magic number (MSB first) |
| 0004 | 32 bit integer | 60000 | number of items |
| 0008 | unsigned byte | ?? | label |
| 0009 | unsigned byte | ?? | label |
| ….. | ….. | ….. | ….. |
| xxxx | unsigned byte | ?? | label |
Значения меток - от 0 до 9.
Похоже, что первые 8 байт (или первые 2 32-битных целых числа) можно пропустить, поскольку они содержат метаданные файла, которые обычно полезны для языков программирования нижнего уровня. Чтобы разобрать файл, мы можем выполнить следующие операции:
- Откройте файл с помощью библиотеки gzip, чтобы мы могли распаковать файл
- Считываем весь массив байтов в память
- Отбросить первые 8 байт
- Итерация над каждым байтом и приведение байта к целому числу
ПРИМЕЧАНИЕ: Если бы этот файл не был получен из надежного источника, потребовалось бы сделать гораздо больше проверок. Для целей этой статьи в блоге я буду считать, что файл действителен в своей целостности.
В [3]:
with gzip.open('train-labels-idx1-ubyte.gz') as train_labels:
data_from_train_file = train_labels.read()
# Skip the first 8 bytes, we know exactly how many labels there are
label_data = data_from_train_file[8:]
assert len(label_data) == 60000
# Convert every byte to an integer. This will be a number between 0 and 9
labels = [int(label_byte) for label_byte in label_data]
assert min(labels) == 0 and max(labels) == 9
assert len(labels) == 60000
Чтение изображений
| [offset] | [type] | [value] | [description] |
| 0000 | 32 bit integer | 0x00000803(2051) | magic number |
| 0004 | 32 bit integer | 60000 | number of images |
| 0008 | 32 bit integer | 28 | number of rows |
| 0012 | 32 bit integer | 28 | number of columns |
| 0016 | unsigned byte | ?? | pixel |
| 0017 | unsigned byte | ?? | pixel |
| ….. | ….. | ….. | ….. |
| xxxx | unsigned byte | ?? | pixel |
Чтение изображений несколько отличается от чтения этикеток. Первые 16 байт содержат метаданные, которые нам уже известны. Мы можем пропустить эти байты и перейти непосредственно к чтению изображений. Каждое изображение представлено в виде массива байтов 28*28 без знака. Все, что нам нужно сделать, это прочитать одно изображение за раз и сохранить его в массиве.
В [4]:
SIZE_OF_ONE_IMAGE = 28 ** 2
images = []
# Iterate over the train file, and read one image at a time
with gzip.open('train-images-idx3-ubyte.gz') as train_images:
train_images.read(4 * 4)
ctr = 0
for _ in range(60000):
image = train_images.read(size=SIZE_OF_ONE_IMAGE)
assert len(image) == SIZE_OF_ONE_IMAGE
# Convert to numpy
image_np = np.frombuffer(image, dtype='uint8') / 255
images.append(image_np)
images = np.array(images)
images.shape
Выход [4]: (60000, 784)
Список наших изображений теперь содержит 60 000 изображений. Каждое изображение представлено в виде байтового вектора SIZE_OF_ONE_IMAGE Попробуем построить график изображения с помощью библиотеки matplotlib:
В [5]:
def plot_image(pixels: np.array):
plt.imshow(pixels.reshape((28, 28)), cmap='gray')
plt.show()
plot_image(images[25])
Кодирование меток изображений с помощью одноточечного кодирования
Мы собираемся использовать Одновременное кодирование для преобразования наших целевых меток в вектор.
В [6]:
labels_np = np.array(labels).reshape((-1, 1))
encoder = OneHotEncoder(categories='auto')
labels_np_onehot = encoder.fit_transform(labels_np).toarray()
labels_np_onehot
Выход [6]:
array([[0., 0., 0., ..., 0., 0., 0.],
[1., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 1., 0.]])
Мы успешно создали входные и выходные векторы, которые будут подаваться на входной и выходной слои нашей нейронной сети. Входной вектор с индексом i будет соответствовать выходному вектору с индексом i
В [7]:
labels_np_onehot[999]
Выход [7]:
array([0., 0., 0., 0., 0., 0., 1., 0., 0., 0.])
В [8]:
plot_image(images[999])

В примере выше мы видим, что изображение с индексом 999 четко представляет 6. Связанный с ним выходной вектор содержит 10 цифр (поскольку имеется 10 доступных меток), и цифра с индексом 6 устанавливается в 1, указывая, что это правильная метка.
Построение тренировочного и тестового сплита
Для того чтобы проверить, правильно ли обучена наша ИНС, мы берем определенный процент обучающего набора данных (60 000 изображений) и откладываем его для тестирования.
В [9]:
X_train, X_test, y_train, y_test = train_test_split(images, labels_np_onehot)
В [10]:
y_train.shape
Выход [10]:
(45000, 10)
В [11]:
y_test.shape
Выход [11]:
(15000, 10)
Как видите, наш набор данных из 60 000 изображений был разделен на один набор данных из 45 000 изображений и другой из 15 000 изображений.
Обучение нейронной сети с помощью Keras
В [12]:
model = keras.Sequential()
model.add(keras.layers.Dense(input_shape=(SIZE_OF_ONE_IMAGE,), units=128, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.summary()
model.compile(optimizer='sgd',
loss='categorical_crossentropy',
metrics=['accuracy'])
| Layer (type) | Output Shape | Param # |
| dense (Dense) | (None, 128) | 100480 |
| dense_1 (Dense) | (None, 10) | 1290 |
Общие параметры: 101,770
Обучаемые параметры: 101 770
Необучаемые параметры: 0
В [13]:
X_train.shape
Выход [13]:
(45000, 784)
В [14]:
model.fit(X_train, y_train, epochs=20, batch_size=128)
Epoch 1/20
45000/45000 [==============================] - 8s 169us/step - loss: 1.3758 - acc: 0.6651
Epoch 2/20
45000/45000 [==============================] - 7s 165us/step - loss: 0.6496 - acc: 0.8504
Epoch 3/20
45000/45000 [==============================] - 8s 180us/step - loss: 0.4972 - acc: 0.8735
Epoch 4/20
45000/45000 [==============================] - 9s 191us/step - loss: 0.4330 - acc: 0.8858
Epoch 5/20
45000/45000 [==============================] - 8s 186us/step - loss: 0.3963 - acc: 0.8931
Epoch 6/20
45000/45000 [==============================] - 8s 183us/step - loss: 0.3714 - acc: 0.8986
Epoch 7/20
45000/45000 [==============================] - 8s 182us/step - loss: 0.3530 - acc: 0.9028
Epoch 8/20
45000/45000 [==============================] - 9s 191us/step - loss: 0.3387 - acc: 0.9055
Epoch 9/20
45000/45000 [==============================] - 8s 175us/step - loss: 0.3266 - acc: 0.9091
Epoch 10/20
45000/45000 [==============================] - 9s 199us/step - loss: 0.3163 - acc: 0.9117
Epoch 11/20
45000/45000 [==============================] - 8s 185us/step - loss: 0.3074 - acc: 0.9140
Epoch 12/20
45000/45000 [==============================] - 10s 214us/step - loss: 0.2991 - acc: 0.9162
Epoch 13/20
45000/45000 [==============================] - 8s 187us/step - loss: 0.2919 - acc: 0.9185
Epoch 14/20
45000/45000 [==============================] - 9s 202us/step - loss: 0.2851 - acc: 0.9203
Epoch 15/20
45000/45000 [==============================] - 9s 201us/step - loss: 0.2788 - acc: 0.9222
Epoch 16/20
45000/45000 [==============================] - 9s 206us/step - loss: 0.2730 - acc: 0.9241
Epoch 17/20
45000/45000 [==============================] - 7s 164us/step - loss: 0.2674 - acc: 0.9254
Epoch 18/20
45000/45000 [==============================] - 9s 189us/step - loss: 0.2622 - acc: 0.9271
Epoch 19/20
45000/45000 [==============================] - 10s 219us/step - loss: 0.2573 - acc: 0.9286
Epoch 20/20
45000/45000 [==============================] - 9s 197us/step - loss: 0.2526 - acc: 0.9302
Выход [14]:
<tensorflow.python.keras.callbacks.History at 0x1129f1f28>>
В [15]:
model.evaluate(X_test, y_test)
15000/15000 [==============================] - 2с 158ус/шаг
Выход [15]:
[0.2567395991722743, 0.9264]
Просмотр результатов
Поздравляем! Вы только что обучили нейронную сеть для предсказания рукописных цифр с точностью более 90%! Давайте протестируем сеть на одной из картинок, имеющихся в нашем тестовом наборе
Возьмем случайное изображение, в данном случае изображение с индексом 1010. Возьмем предсказанную метку (в данном случае значение равно 4, поскольку 5-й индекс установлен на 1)
В [16]:
y_test[1010]
Выход [16]:
array([0., 0., 0., 0., 1., 0., 0., 0., 0., 0.])
Построим график изображения соответствующего изображения
В [17]:
plot_image(X_test[1010])
Понимание выхода активационного слоя softmax
Теперь давайте пропустим это число через нейронную сеть и посмотрим, как выглядит наш предсказанный выход!
В [18]:
predicted_results = model.predict(X_test[1010].reshape((1, -1)))
Выход слоя softmax - это распределение вероятности для каждого выхода. В нашем случае существует 10 возможных выходов (цифры 0-9). Конечно, ожидается, что каждое из наших изображений будет соответствовать только одному определенному выходу (другими словами, все наши изображения будут содержать только одну определенную цифру).
Поскольку это распределение вероятности, сумма предсказанных результатов равна ~1.0
В [19]:
predicted_results.sum()
Выход [19]:
1.0000001
Считывание выхода активационного слоя softmax для нашей цифры
Как вы можете видеть ниже, 7-й индекс очень близок к 1 (0,9), что означает, что существует 90% вероятность того, что эта цифра - 6... что и произошло! Поздравляем!
В [20]:
predicted_results
Выход [20]:
array([[1.2202066e-06, 3.4432333e-08, 3.5151488e-06, 1.2011528e-06,
9.9889344e-01, 3.5855610e-05, 1.6140550e-05, 7.6822333e-05,
1.0446112e-04, 8.6736667e-04]], dtype=float32)
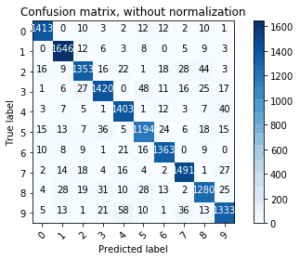
Просмотр матрицы путаницы
В [21]:
predicted_outputs = np.argmax(model.predict(X_test), axis=1)
expected_outputs = np.argmax(y_test, axis=1)
predicted_confusion_matrix = confusion_matrix(expected_outputs, predicted_outputs)
В [22]:
predicted_confusion_matrix
Выход [22]:
array([[1413, 0, 10, 3, 2, 12, 12, 2, 10, 1],
[ 0, 1646, 12, 6, 3, 8, 0, 5, 9, 3],
[ 16, 9, 1353, 16, 22, 1, 18, 28, 44, 3],
[ 1, 6, 27, 1420, 0, 48, 11, 16, 25, 17],
[ 3, 7, 5, 1, 1403, 1, 12, 3, 7, 40],
[ 15, 13, 7, 36, 5, 1194, 24, 6, 18, 15],
[ 10, 8, 9, 1, 21, 16, 1363, 0, 9, 0],
[ 2, 14, 18, 4, 16, 4, 2, 1491, 1, 27],
[ 4, 28, 19, 31, 10, 28, 13, 2, 1280, 25],
[ 5, 13, 1, 21, 58, 10, 1, 36, 13, 1333]])
В [23]:
# Source code: https://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
# Compute confusion matrix
class_names = [str(idx) for idx in range(10)]
cnf_matrix = confusion_matrix(expected_outputs, predicted_outputs)
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names,
title='Confusion matrix, without normalization')
plt.show()
Заключение
В этом учебнике вы познакомились с несколькими важными концепциями, которые являются основополагающими для работы в Machine Learning. Мы узнали, как:
- Кодирование и декодирование изображений в наборе данных MNIST
- Кодирование категориальных признаков с помощью одноточечного кодирования
- Определите нашу нейронную сеть с 2 скрытыми слоями и выходным слоем, использующим функцию активации softmax
- Исследуйте результаты вывода функции активации softmax
- Постройте матрицу смешения нашего классификатора
Такие библиотеки, как Sci-Kit Learn и Keras, существенно снизили входной барьер для машинного обучения - так же, как Python снизил планку входа в программирование в целом. Конечно, для освоения все еще требуются годы (или десятилетия) работы!
Инженеры, понимающие машинное обучение пользуются большим спросом. С помощью библиотек, о которых я говорил выше, и вводных статей в блогах, посвященных практическому машинному обучению (как эта), все инженеры должны быть в состоянии освоить машинное обучение, даже если они не понимают полного теоретического обоснования конкретной модели, библиотеки или фреймворка. И, надеюсь, они будут использовать эти навыки для улучшения того, что они создают каждый день.
Если мы начнем делать наши компоненты немного умнее и немного более персонализированными каждый день, мы сможем сделать клиентов более вовлеченными и находящимися в центре всего, что мы создаем.
Back to Top