NumPy, SciPy и pandas: взаимосвязь с Python

Оглавление

• Корреляция
• Пример: Вычисление корреляции NumPy
• Пример: Вычисление корреляции SciPy
• Пример: Расчет корреляции панд
• Линейная корреляция
  • Коэффициент корреляции Пирсона
  • Линейная регрессия: реализация SciPy
  • Корреляция Пирсона: реализация NumPy и SciPy
  • Корреляция Пирсона: внедрение pandas
• Ранговая корреляция
  • Коэффициент корреляции Спирмена
  • Коэффициент корреляции Кендалла
  • Ранг: Реализация SciPy
  • Ранговая корреляция: реализация NumPy и SciPy
  • Ранговая корреляция: внедрение pandas
• Визуализация корреляции
  • Графики X-Y с линией регрессии
  • Тепловые карты корреляционных матриц
• Заключение

Коэффициенты корреляции количественно определяют связь между переменными или особенностями набора данных. Эти статистические данные имеют большое значение для науки и техники, и в Python есть отличные инструменты, которые вы можете использовать для их расчета. SciPy, NumPy и pandas методы корреляции являются быстрыми, всеобъемлющими и хорошо документированными.

В этом уроке вы узнаете:

• Каковы коэффициенты корреляции Пирсона, Спирмена и Кендалла
• Как использовать SciPy, NumPy и pandas корреляционные функции
• Как визуализировать данные, линии регрессии и корреляционные матрицы с помощью Matplotlib

Вы начнете с объяснения корреляции, затем увидите три кратких вводных примера и, наконец, углубитесь в детали корреляции NumPy, SciPy и pandas.

Корреляция

Статистика и наука о данных часто исследуют взаимосвязи между двумя или более переменными (или функциями) набора данных. Каждая точка данных в наборе данных является наблюдением, а объектов являются свойствами или атрибутами этих наблюдений.

В каждом наборе данных, с которым вы работаете, используются переменные и наблюдения. Например, вам может быть интересно понять следующее:

• Как рост баскетболистов соотносится с их точностью стрельбы
• Существует ли взаимосвязь между опытом работы сотрудника и заработной платой
• Какая математическая зависимость существует между плотностью населения и валовым внутренним продуктом разных стран

В приведенных выше примерах рост, точность стрельбы, стаж работы, зарплата, плотность населения и валовой внутренний продукт являются характеристиками или переменными. Данные, относящиеся к каждому игроку, сотруднику и каждой стране, являются наблюдениями.

Когда данные представлены в виде таблицы, строки этой таблицы обычно представляют собой наблюдения, а столбцы - характеристики. Взгляните на эту таблицу сотрудников:

Name	Years of Experience	Annual Salary
Ann	30	120,000
Rob	21	105,000
Tom	19	90,000
Ivy	10	82,000

В этой таблице каждая строка представляет одно наблюдение или данные об одном сотруднике (Энн, Робе, Томе или Айви). В каждом столбце указано одно свойство или характеристика (имя, опыт работы или зарплата) для всех сотрудников.

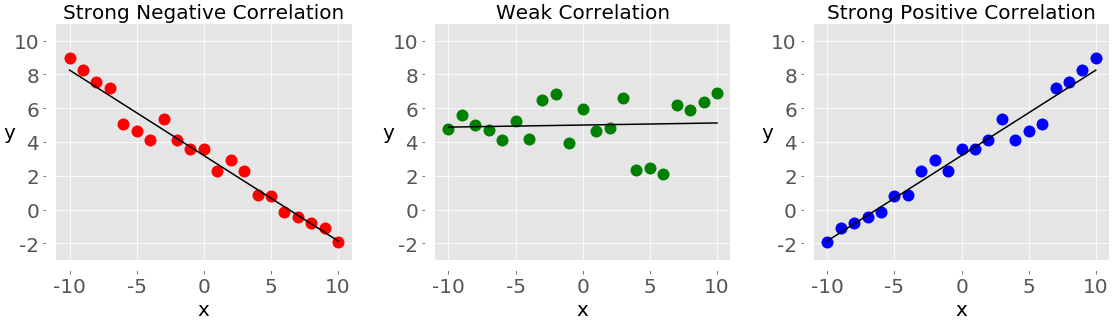
Если вы проанализируете любые два признака в наборе данных, то обнаружите некоторую корреляцию между этими двумя признаками. Обратите внимание на следующие рисунки:

Каждый из этих графиков показывает одну из трех различных форм корреляции:

1. Отрицательная корреляция (красные точки): На графике слева значения y имеют тенденцию к уменьшению по мере увеличения значений x. Это показывает сильную отрицательную корреляцию, которая возникает, когда большие значения одного признака соответствуют малым значениям другого, и наоборот.

2. Слабая корреляция или ее отсутствие (зеленые точки): График в середине не показывает явного тренда. Это форма слабой корреляции, которая возникает, когда связь между двумя признаками неочевидна или едва заметна.

3. Положительная корреляция (синие точки): На графике справа значения y имеют тенденцию к увеличению по мере увеличения значений x. Это иллюстрирует сильную положительную корреляцию, которая возникает, когда большие значения одного признака соответствуют большим значениям другого, и наоборот.

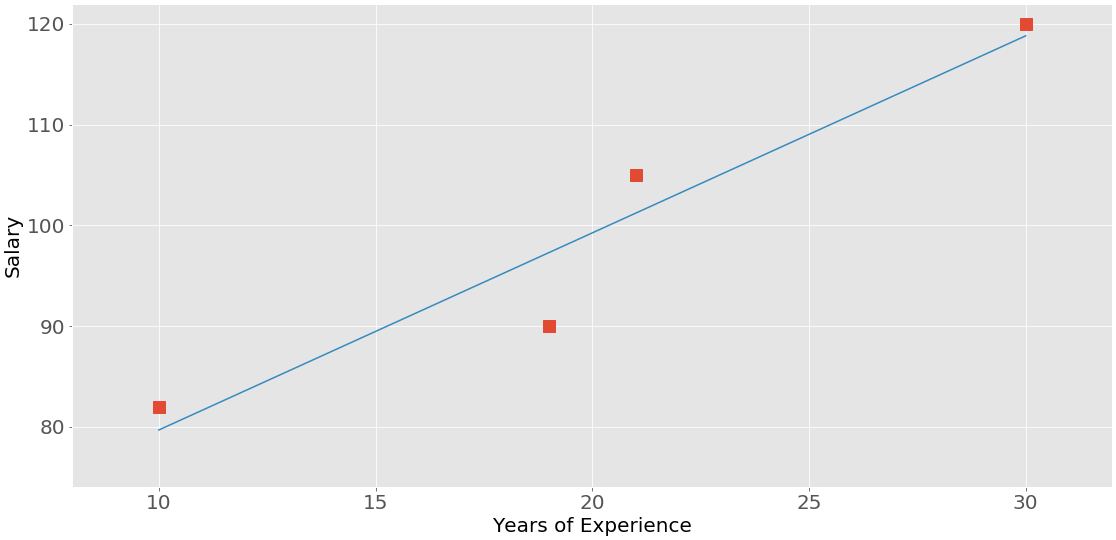
На следующем рисунке представлены данные из приведенной выше таблицы сотрудников:

Корреляция между опытом и зарплатой положительная, поскольку более высокий опыт соответствует более высокой зарплате, и наоборот.

Примечание: Когда вы анализируете корреляцию, вы всегда должны иметь в виду, что корреляция не указывает на причинно-следственную связь. Он количественно определяет силу взаимосвязи между объектами набора данных. Иногда связь вызывается фактором, общим для нескольких интересующих объектов.

Корреляция тесно связана с другими статистическими величинами, такими как среднее значение, стандартное отклонение, дисперсия и ковариация. Если вы хотите узнать больше об этих величинах и о том, как их рассчитать с помощью Python, ознакомьтесь с Описательной статистикой с помощью Python.

Существует несколько статистических данных, которые можно использовать для количественной оценки корреляции. В этом руководстве вы узнаете о трех коэффициентах корреляции:

• Пирсоновский р
• Ро копейщика
• Тау Кендалла

Коэффициент Пирсона измеряет линейную корреляцию, в то время как коэффициенты Спирмена и Кендалла сравнивают ранги данных. Существует несколько корреляционных функций и методов NumPy, SciPy и pandas, которые можно использовать для вычисления этих коэффициентов. Вы также можете использовать Matplotlib для удобной иллюстрации результатов.

Пример: Вычисление числовой корреляции

В NumPy есть множество статистических процедур, включая np.corrcoef(), которые возвращают матрицу коэффициентов корреляции Пирсона. Вы можете начать с импорта NumPy и определения двух массивов NumPy. Это экземпляры класса ndarray. Назовем их x и y:

>>> import numpy as np
>>> x = np.arange(10, 20)
>>> x
array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
array([ 2,  1,  4,  5,  8, 12, 18, 25, 96, 48])

Здесь вы используете np.arange() для создания массива x из целых чисел от 10 (включительно) до 20 (исключая). Затем вы используете np.array() для создания второго массива y, содержащего произвольные целые числа.

Если у вас есть два массива одинаковой длины, вы можете вызвать np.corrcoef(), используя оба массива в качестве аргументов:

>>> r = np.corrcoef(x, y)
>>> r
array([[1.        , 0.75864029],
       [0.75864029, 1.        ]])
>>> r[0, 1]
0.7586402890911867
>>> r[1, 0]
0.7586402890911869

corrcoef() возвращает корреляционную матрицу, которая представляет собой двумерный массив с коэффициентами корреляции. Вот упрощенная версия корреляционной матрицы, которую вы только что создали:

        x       y

x    1.00    0.76
y    0.76    1.00

Значения на главной диагонали корреляционной матрицы (верхний левый и нижний правый) равны 1. Верхнее левое значение соответствует коэффициенту корреляции для x и x, в то время как нижнее правое значение соответствует коэффициенту корреляции для y и y. Они всегда равны 1.

Однако обычно вам нужны нижние левые и верхние правые значения корреляционной матрицы. Эти значения равны и оба представляют собой Коэффициент корреляции Пирсона для x и y. В данном случае это примерно 0,76.

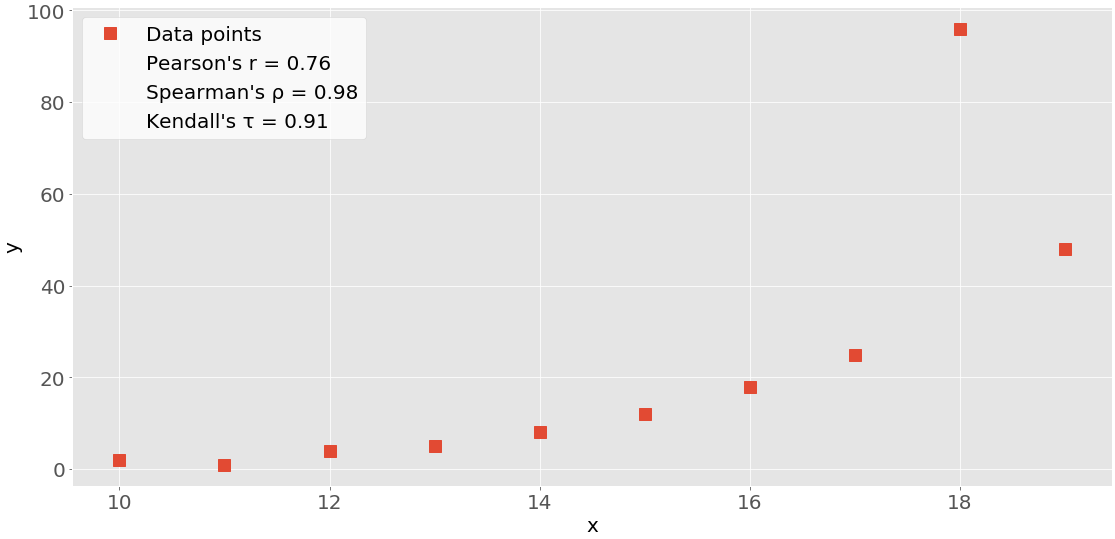
На этом рисунке показаны точки данных и коэффициенты корреляции для приведенного выше примера:

Красные квадраты - это точки данных. Как вы можете видеть, на рисунке также показаны значения трех коэффициентов корреляции.

Пример: Вычисление корреляции SciPy

SciPy также имеет множество статистических процедур, содержащихся в scipy.stats. Вы можете использовать следующие методы для расчета трех коэффициентов корреляции, которые вы видели ранее:

• pearsonr()
• spearmanr()
• kendalltau()

Вот как бы вы использовали эти функции в Python:

>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> scipy.stats.pearsonr(x, y)    # Pearson's r
(0.7586402890911869, 0.010964341301680832)
>>> scipy.stats.spearmanr(x, y)   # Spearman's rho
SpearmanrResult(correlation=0.9757575757575757, pvalue=1.4675461874042197e-06)
>>> scipy.stats.kendalltau(x, y)  # Kendall's tau
KendalltauResult(correlation=0.911111111111111, pvalue=2.9761904761904762e-05)

Обратите внимание, что эти функции возвращают объекты, содержащие два значения:

1. Коэффициент корреляции
2. p-значение

В статистических методах при проверке гипотезы используется p-значение. P-значение является важным показателем, для интерпретации которого требуются глубокие знания в области вероятности и статистики. Чтобы узнать о них больше, вы можете прочитать о основах или ознакомиться с объяснением p-значений специалистом по обработке данных.

Вы можете извлечь p-значения и коэффициенты корреляции с их индексами, как элементы кортежей :

>>> scipy.stats.pearsonr(x, y)[0]    # Pearson's r
0.7586402890911869
>>> scipy.stats.spearmanr(x, y)[0]   # Spearman's rho
0.9757575757575757
>>> scipy.stats.kendalltau(x, y)[0]  # Kendall's tau
0.911111111111111

Вы также можете использовать точечную запись для коэффициентов Спирмена и Кендалла:

>>> scipy.stats.spearmanr(x, y).correlation   # Spearman's rho
0.9757575757575757
>>> scipy.stats.kendalltau(x, y).correlation  # Kendall's tau
0.911111111111111

Точечная запись длиннее, но она также более удобочитаема и не требует пояснений.

Если вы хотите получить коэффициент корреляции Пирсона и p-значение одновременно, то вы можете распаковать возвращаемое значение:

>>> r, p = scipy.stats.pearsonr(x, y)
>>> r
0.7586402890911869
>>> p
0.010964341301680829

Этот подход использует распаковку Python и тот факт, что pearsonr() возвращает кортеж с этими двумя статистическими данными. Вы также можете использовать этот прием с spearmanr() и kendalltau(), как вы увидите позже.

Пример: Расчет корреляции панд

pandas в некоторых случаях более удобен для расчета статистики, чем NumPy и SciPy. Он предлагает статистические методы для экземпляров Series и DataFrame. Например, при наличии двух объектов Series с одинаковым количеством элементов вы можете вызвать .corr() для одного из них, указав другой в качестве первого аргумента:

>>> import pandas as pd
>>> x = pd.Series(range(10, 20))
>>> x
0    10
1    11
2    12
3    13
4    14
5    15
6    16
7    17
8    18
9    19
dtype: int64
>>> y = pd.Series([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
0     2
1     1
2     4
3     5
4     8
5    12
6    18
7    25
8    96
9    48
dtype: int64
>>> x.corr(y)                     # Pearson's r
0.7586402890911867
>>> y.corr(x)
0.7586402890911869
>>> x.corr(y, method='spearman')  # Spearman's rho
0.9757575757575757
>>> x.corr(y, method='kendall')   # Kendall's tau
0.911111111111111

Здесь вы используете .corr() для вычисления всех трех коэффициентов корреляции. Вы определяете желаемую статистику с помощью параметра method, который может принимать одно из нескольких значений:

• 'pearson'
• 'spearman'
• 'kendall'
• вызываемый объект

Вызываемым может быть любая функция, метод или объект с .__call__(), который принимает два одномерных создает массивы и возвращает число с плавающей запятой.

Линейная корреляция

Линейная корреляция измеряет близость математической зависимости между переменными или элементами набора данных к линейной функции. Если взаимосвязь между двумя признаками ближе к некоторой линейной функции, то их линейная корреляция сильнее и абсолютное значение коэффициента корреляции выше.

Коэффициент корреляции Пирсона

Рассмотрим набор данных с двумя характеристиками: x и y. Каждый объект имеет n значений, поэтому x и y являются n-кортежами. Допустим, что первое значение x₁ из x соответствует первому значению y₁ из y, второму значению x₂ из x ко второму значению y₂ из y и так далее. Далее, имеется n пар соответствующих значений: (x₁, y₁), (x₂, y₂) и так далее. Каждая из этих пар x-y представляет собой одно наблюдение.

Коэффициент корреляции Пирсона (произведение-момент) является мерой линейной зависимости между двумя признаками. Это отношение ковариации x и y к произведению их стандартных отклонений. Его часто обозначают буквой r и называют r Пирсона. Математически это значение можно выразить следующим уравнением:

р = Σᵢ((xᵢ − значит(х))(yᵢ − означает(г))) (√Σᵢ(xᵢ − значит(х))2 √Σᵢ(yᵢ − означает(г))2)-1

Здесь i принимает значения 1, 2, ..., n. средние значения из x и y обозначаются как среднее(x) и усредненное значение(y). Эта формула показывает, что если большие значения x, как правило, соответствуют большим значениям y и наоборот, то r положительно. С другой стороны, если большие значения x в основном связаны с меньшими значениями y и наоборот, то r отрицательно.

Вот несколько важных фактов о коэффициенте корреляции Пирсона:

• Коэффициент корреляции Пирсона может принимать любое реальное значение в диапазоне -1 ≤ r ≤ 1.

• Максимальное значение r = 1 соответствует случаю, в котором существует идеальная положительная линейная зависимость между x и y. Другими словами, большие значения x соответствуют большим значениям y и наоборот.

• Значение r > 0 указывает на положительную корреляцию между x и y.

• Значение r = 0 соответствует случаю, в котором нет линейной зависимости между x и y.

• Значение r <0 указывает на отрицательную корреляцию между x и y.

• Минимальное значение r = -1 соответствует случаю, когда существует идеальная отрицательная линейная зависимость между x и y. Другими словами, большие значения x соответствуют меньшим значениям y и наоборот.

Приведенные выше факты можно свести в следующую таблицу:

Pearson’s r Value	Correlation Between x and y
equal to 1	perfect positive linear relationship
greater than 0	positive correlation
equal to 0	no linear relationship
less than 0	negative correlation
equal to -1	perfect negative linear relationship

Короче говоря, большее абсолютное значение r указывает на более сильную корреляцию, более близкую к линейной функции. Меньшее абсолютное значение r указывает на более слабую корреляцию.

Линейная регрессия: реализация SciPy

Линейная регрессия - это процесс нахождения линейной функции, которая максимально приближена к фактической взаимосвязи между признаками. Другими словами, вы определяете линейную функцию, которая наилучшим образом описывает связь между признаками. Эта линейная функция также называется линией регрессии .

Вы можете реализовать линейную регрессию с помощью SciPy. Вы получите линейную функцию, которая наилучшим образом аппроксимирует взаимосвязь между двумя массивами, а также коэффициент корреляции Пирсона. Чтобы начать, вам сначала нужно импортировать библиотеки и подготовить некоторые данные для работы:

>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])

Здесь вы импортируете numpy и scipy.stats и определяете переменные x и y.

Вы можете использовать scipy.stats.linregress() для выполнения линейной регрессии для двух массивов одинаковой длины. Вы должны указать массивы в качестве аргументов и получить выходные данные, используя точечную запись:

>>> result = scipy.stats.linregress(x, y)
>>> result.slope
7.4363636363636365
>>> result.intercept
-85.92727272727274
>>> result.rvalue
0.7586402890911869
>>> result.pvalue
0.010964341301680825
>>> result.stderr
2.257878767543913

Вот и все! Вы завершили линейную регрессию и получили следующие результаты:

• .slope: наклон линии регрессии
• .intercept: точка пересечения линии регрессии
• .pvalue: значение p
• .stderr: стандартная ошибка расчетного градиента

В следующем разделе вы узнаете, как визуализировать эти результаты.

Вы также можете указать единственный аргумент для linregress(), но это должен быть двумерный массив с одним измерением длиной два:

>>> xy = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
...                [2, 1, 4, 5, 8, 12, 18, 25, 96, 48]])
>>> scipy.stats.linregress(xy)
LinregressResult(slope=7.4363636363636365, intercept=-85.92727272727274, rvalue=0.7586402890911869, pvalue=0.010964341301680825, stderr=2.257878767543913)

Результат в точности такой же, как в предыдущем примере, потому что xy содержит те же данные, что и x и y вместе взятые. linregress() взял первую строку из xy как один элемент, а второй ряд - как другой элемент.

Примечание: В приведенном выше примере scipy.stats.linregress() строки рассматриваются как объекты, а столбцы - как наблюдения. Это потому, что строк всего две.

Обычная практика в машинном обучении заключается в обратном: строки - это наблюдения, а столбцы - объекты. Многие библиотеки машинного обучения, такие как pandas, Scikit-Learn, Keras и другие, следуют этому соглашению.

При анализе корреляции в наборе данных следует обращать внимание на то, как указаны наблюдения и особенности.

linregress() вернет тот же результат, если вы зададите транспонировать из xy или числовой массив с 10 строками и двумя столбцами. В NumPy вы можете транспонировать матрицу многими способами:

• transpose()
• .transpose()
• .T

Вот как вы могли бы перенести xy:

>>> xy.T
array([[10,  2],
       [11,  1],
       [12,  4],
       [13,  5],
       [14,  8],
       [15, 12],
       [16, 18],
       [17, 25],
       [18, 96],
       [19, 48]])

Теперь, когда вы знаете, как выполнить транспонирование, вы можете передать его в linregress(). В первом столбце будет отображаться один объект, а во втором - другой:

>>> scipy.stats.linregress(xy.T)
LinregressResult(slope=7.4363636363636365, intercept=-85.92727272727274, rvalue=0.7586402890911869, pvalue=0.010964341301680825, stderr=2.257878767543913)

Здесь вы используете .T, чтобы получить транспонирование xy. linregress() аналогично работает с xy и его транспонированием. Он извлекает объекты, разбивая массив по измерению длиной два.

Вам также следует внимательно отнестись к тому, содержит ли ваш набор данных пропущенные значения. В области науки о данных и машинного обучения вы часто будете сталкиваться с отсутствующими или поврежденными данными. Обычный способ представить это в Python, NumPy, SciPy и pandas - использовать NaN или , а не числовые значения. Но если ваши данные содержат nan значений, то вы не получите полезного результата с помощью linregress():

>>> scipy.stats.linregress(np.arange(3), np.array([2, np.nan, 5]))
LinregressResult(slope=nan, intercept=nan, rvalue=nan, pvalue=nan, stderr=nan)

В этом случае результирующий объект возвращает все значения nan. В Python nan - это специальное значение с плавающей запятой, которое можно получить, используя любое из следующих значений:

• float('nan')
• math.nan
• numpy.nan

Вы также можете проверить, соответствует ли переменная nan с помощью math.isnan() или numpy.isnan().

Корреляция Пирсона: реализация NumPy и SciPy

Вы уже видели, как получить коэффициент корреляции Пирсона с помощью corrcoef() и pearsonr():

>>> r, p = scipy.stats.pearsonr(x, y)
>>> r
0.7586402890911869
>>> p
0.010964341301680829
>>> np.corrcoef(x, y)
array([[1.        , 0.75864029],
       [0.75864029, 1.        ]])

Обратите внимание, что если вы укажете в массиве значение от nan до pearsonr(), то получите ValueError.

Есть несколько дополнительных деталей, заслуживающих внимания. Во-первых, напомним, что np.corrcoef() может принимать в качестве аргументов два массива NumPy. Вместо этого вы можете передать один двумерный массив с теми же значениями, что и в аргументе:

>>> np.corrcoef(xy)
array([[1.        , 0.75864029],
       [0.75864029, 1.        ]])

В этом и предыдущих примерах результаты одинаковы. И снова первая строка xy представляет один объект, а вторая строка - другой.

Если вы хотите получить коэффициенты корреляции для трех объектов, то вы просто предоставляете числовой двумерный массив с тремя строками в качестве аргумента:

>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
...                 [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
...                 [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])
>>> np.corrcoef(xyz)
array([[ 1.        ,  0.75864029, -0.96807242],
       [ 0.75864029,  1.        , -0.83407922],
       [-0.96807242, -0.83407922,  1.        ]])

Вы снова получите корреляционную матрицу, но эта матрица будет больше предыдущих:

         x        y        z

x     1.00     0.76    -0.97
y     0.76     1.00    -0.83
z    -0.97    -0.83     1.00

Это связано с тем, что corrcoef() рассматривает каждую строку из xyz как один признак. Значение 0.76 является коэффициентом корреляции для первых двух признаков из xyz. Это то же самое, что и коэффициент для x и y в предыдущих примерах. -0.97 представляет собой r Пирсона для первого и третьего признаков, в то время как -0.83 - это r Пирсона для последнего две особенности.

Вот интересный пример того, что происходит, когда вы передаете nan данные в corrcoef():

>>> arr_with_nan = np.array([[0, 1, 2, 3],
...                          [2, 4, 1, 8],
...                          [2, 5, np.nan, 2]])
>>> np.corrcoef(arr_with_nan)
array([[1.        , 0.62554324,        nan],
       [0.62554324, 1.        ,        nan],
       [       nan,        nan,        nan]])

В этом примере первые две строки (или объекты) arr_with_nan в порядке, но третья строка [2, 5, np.nan, 2] содержит значение nan. Все, что не включает функцию с nan, рассчитывается правильно. Однако результаты, зависящие от последней строки, следующие nan.

По умолчанию numpy.corrcoef() рассматривает строки как объекты, а столбцы - как наблюдения. Если вам нужно противоположное поведение, которое широко используется в машинном обучении, то используйте аргумент rowvar=False:

>>> xyz.T
array([[ 10,   2,   5],
       [ 11,   1,   3],
       [ 12,   4,   2],
       [ 13,   5,   1],
       [ 14,   8,   0],
       [ 15,  12,  -2],
       [ 16,  18,  -8],
       [ 17,  25, -11],
       [ 18,  96, -15],
       [ 19,  48, -16]])
>>> np.corrcoef(xyz.T, rowvar=False)
array([[ 1.        ,  0.75864029, -0.96807242],
       [ 0.75864029,  1.        , -0.83407922],
       [-0.96807242, -0.83407922,  1.        ]])

Этот массив идентичен тому, который вы видели ранее. Здесь вы применяете другое соглашение, но результат тот же.

Корреляция Пирсона: реализация pandas

До сих пор вы использовали объектные методы Series и DataFrame для вычисления коэффициентов корреляции. Давайте рассмотрим эти методы более подробно. Сначала вам нужно импортировать pandas и создать несколько экземпляров Series и DataFrame:

>>> import pandas as pd
>>> x = pd.Series(range(10, 20))
>>> x
0    10
1    11
2    12
3    13
4    14
5    15
6    16
7    17
8    18
9    19
dtype: int64
>>> y = pd.Series([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
0     2
1     1
2     4
3     5
4     8
5    12
6    18
7    25
8    96
9    48
dtype: int64
>>> z = pd.Series([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
>>> z
0     5
1     3
2     2
3     1
4     0
5    -2
6    -8
7   -11
8   -15
9   -16
dtype: int64
>>> xy = pd.DataFrame({'x-values': x, 'y-values': y})
>>> xy
   x-values  y-values
0        10         2
1        11         1
2        12         4
3        13         5
4        14         8
5        15        12
6        16        18
7        17        25
8        18        96
9        19        48
>>> xyz = pd.DataFrame({'x-values': x, 'y-values': y, 'z-values': z})
>>> xyz
   x-values  y-values  z-values
0        10         2         5
1        11         1         3
2        12         4         2
3        13         5         1
4        14         8         0
5        15        12        -2
6        16        18        -8
7        17        25       -11
8        18        96       -15
9        19        48       -16

Теперь у вас есть три Series объекта с именами x, y, и z. У вас также есть два объекта DataFrame, xy и xyz.

Примечание: Когда вы работаете с DataFrame экземплярами, вы должны знать, что строки являются наблюдениями, а столбцы - объектами. Это согласуется с обычной практикой машинного обучения.

Вы уже узнали, как использовать .corr() с Series объектами, чтобы получить коэффициент корреляции Пирсона:

>>> x.corr(y)
0.7586402890911867

Здесь вы вызываете .corr() для одного объекта и передаете другой в качестве первого аргумента.

Если вы укажете значение nan, то .corr() все равно будет работать, но это исключит наблюдения, содержащие значения nan:

>>> u, u_with_nan = pd.Series([1, 2, 3]), pd.Series([1, 2, np.nan, 3])
>>> v, w = pd.Series([1, 4, 8]), pd.Series([1, 4, 154, 8])
>>> u.corr(v)
0.9966158955401239
>>> u_with_nan.corr(w)
0.9966158955401239

В этих двух примерах вы получаете одинаковое значение коэффициента корреляции. Это потому, что .corr() игнорирует пару значений (np.nan, 154), в которой отсутствует значение.

Вы также можете использовать .corr() с DataFrame объектами. Вы можете использовать его, чтобы получить корреляционную матрицу для их столбцов:

>>> corr_matrix = xy.corr()
>>> corr_matrix
          x-values  y-values
x-values   1.00000   0.75864
y-values   0.75864   1.00000

Результирующая корреляционная матрица является новым экземпляром DataFrame и содержит коэффициенты корреляции для столбцов xy['x-values'] и xy['y-values']. С такими помеченными результатами обычно очень удобно работать, потому что вы можете получить к ним доступ либо с помощью их меток, либо с помощью целочисленных индексов позиции:

>>> corr_matrix.at['x-values', 'y-values']
0.7586402890911869
>>> corr_matrix.iat[0, 1]
0.7586402890911869

В этом примере показаны два способа доступа к значениям:

1. Используйте .at[] для доступа к одному значению по меткам строк и столбцов.
2. Используйте .iat[] для доступа к значению по позициям его строки и столбца.

Вы можете применить .corr() таким же образом к объектам DataFrame, содержащим три или более столбцов:

>>> xyz.corr()
          x-values  y-values  z-values
x-values  1.000000  0.758640 -0.968072
y-values  0.758640  1.000000 -0.834079
z-values -0.968072 -0.834079  1.000000

Вы получите корреляционную матрицу со следующими коэффициентами корреляции:

• 0.758640 для x-values и y-values
• -0.968072 для x-values и z-values
• -0.834079 для y-values и z-values

Другим полезным методом является .corrwith(),, который позволяет вычислять коэффициенты корреляции между строками или столбцами одного объекта DataFrame и другого объекта Series или DataFrame, передаваемого в качестве первого аргумента :

>>> xy.corrwith(z)
x-values   -0.968072
y-values   -0.834079
dtype: float64

В этом случае результатом будет новый объект Series с коэффициентом корреляции для столбца xy['x-values'] и значениями z, а также коэффициентом для xy['y-values'] и z.

.corrwith() имеет необязательный параметр axis, который определяет, будут ли столбцы или строки представлять объекты. Значение axis по умолчанию равно 0, и по умолчанию также используются столбцы, представляющие объекты. Существует также параметр drop, который указывает, что делать с пропущенными значениями.

Как .corr(), так и .corrwith() имеют необязательный параметр method для указания коэффициента корреляции, который вы хотите рассчитать. Коэффициент корреляции Пирсона возвращается по умолчанию, поэтому в данном случае его указывать не нужно.

Ранговая корреляция

Ранговая корреляция сравнивает ранги или порядок следования данных, относящихся к двум переменным или элементам набора данных. Если порядок следования похож, то корреляция является сильной, положительной и высокой. Однако, если порядок значений близок к обратному, то корреляция сильная, отрицательная и низкая. Другими словами, ранговая корреляция связана только с порядком значений, а не с конкретными значениями из набора данных.

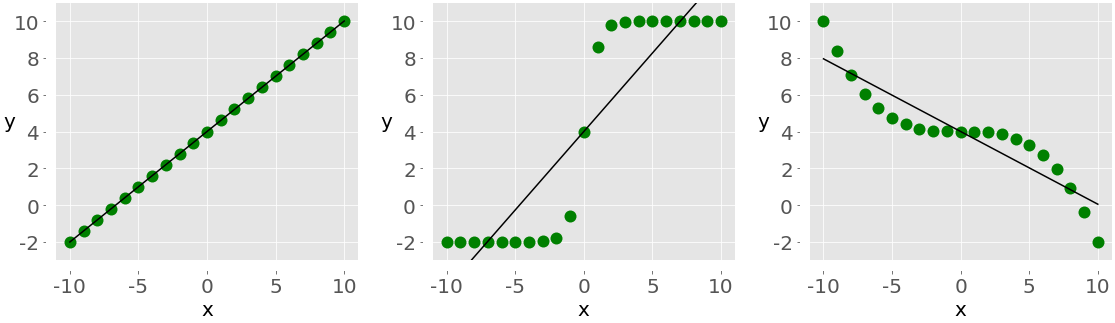
Чтобы проиллюстрировать разницу между линейной и ранговой корреляцией, рассмотрим следующий рисунок:

Левый график имеет идеальную положительную линейную зависимость между x и y, поэтому r = 1. Центральный график показывает положительную корреляцию, а правый - отрицательную. Однако ни один из них не является линейной функцией, поэтому значение r отличается от -1 или 1.

Если смотреть только на порядок или ранги, все три соотношения идеальны! На левом и центральном графиках показаны наблюдения, где большие значения x всегда соответствуют большим значениям y. Это идеальная положительная ранговая корреляция. Правый график иллюстрирует противоположный случай, который представляет собой идеальную отрицательную ранговую корреляцию.

Коэффициент корреляции Спирмена

Коэффициент корреляции Спирмена между двумя признаками - это коэффициент корреляции Пирсона между их ранговыми значениями. Он рассчитывается так же, как и коэффициент корреляции Пирсона, но учитывает их ранги, а не значения. Его часто обозначают греческой буквой rho (ρ) и называют ро Спирмена.

Допустим, у вас есть два n-кортежа, x и y, где (x₁, y₁), (x₂, y₂), … - это наблюдения в виде пар соответствующих значений. Вы можете рассчитать коэффициент корреляции Спирмена ρ таким же образом, как и коэффициент Пирсона. Вы будете использовать ранги вместо фактических значений из x и y.

Вот несколько важных фактов о коэффициенте корреляции Спирмена:

• Оно может принимать реальное значение в диапазоне -1 ≤ ρ ≤ 1.

• Его максимальное значение ρ = 1 соответствует случаю, когда существует монотонно возрастающая функция между x и у. Другими словами, большие значения x соответствуют большим значениям y и наоборот.

• Его минимальное значение ρ = -1 соответствует случаю, когда существует монотонно убывающая функция между x и y. Другими словами, большие значения x соответствуют меньшим значениям y и наоборот.

Вы можете вычислить rho Спирмена в Python очень похожим образом, как и r Пирсона.

Коэффициент корреляции Кендалла

Давайте снова начнем с рассмотрения двух n-кортежей, x и y. Каждая из пар x-y (x₁, y₁), (x₂, y₂), … представляет собой одно наблюдение. Пара наблюдений (xᵢ, yᵢ) и (xⱼ, yⱼ), где i < j, будет одним из трех значений:

• согласных Если (xᵢ &ГТ; xⱼ и yᵢ &ГТ; yⱼ) или (xᵢ &ЛТ; xⱼ и yᵢ &ЛТ; yⱼ)
• несогласный Если (xᵢ &ЛТ; xⱼ и yᵢ &ГТ; yⱼ) или (xᵢ &ГТ; xⱼ и yᵢ &ЛТ; yⱼ)
• ни, если есть ничья в x (xᵢ = xⱼ), ни ничья в y (yᵢ = yⱼ)

Коэффициент корреляции Кендалла сравнивает количество согласующихся и несогласующихся пар данных. Этот коэффициент основан на разнице в количестве согласных и несогласованных пар по отношению к количеству пар x-y. Его часто обозначают греческой буквой тау (τ) и называют тау Кендалла.

Согласно scipy.stats официальным документам, коэффициент корреляции Кендалла рассчитывается как τ = (n⁺ − n⁻) / √((n⁺ + n⁻ + nˣ)(n⁺ + n⁻ + nʸ)), где:

• n⁺ - количество согласных пар
• n⁻ количество несогласованных пар
• nˣ - это количество связей только в x
• nʸ - это количество связей только в y

Если совпадение встречается как в x, так и в y, то оно не включается ни в nˣ, ни в nʸ.

На странице Википедии, посвященной коэффициенту ранговой корреляции Кендалла, приведено следующее выражение: τ = (2 / (n(n − 1))) σᵢⱼ(знак(xᵢ − xⱼ) знак(yᵢ − y ∈)) для i < j, где i = 1, 2, ..., n − 1 и j = 2, 3, ..., n. Знаковая функция sign(z) равна -1, если z < 0, 0, если z = 0, и 1, если z > 0. n(n − 1) / 2 - это общее количество пар x-y.

Ниже приведены некоторые важные факты о коэффициенте корреляции Кендалла:

• Оно может принимать реальное значение в диапазоне -1 ≤ τ ≤ 1.

• Его максимальное значение τ = 1 соответствует случаю, когда ранги соответствующих значений в x и y совпадают. Другими словами, все пары являются согласованными.

• Его минимальное значение τ = -1 соответствует случаю, когда ранжирование в x является обратным ранжированию в y. Другими словами, все пары являются диссонирующими.

Вы можете вычислить tau Кендалла в Python аналогично тому, как вы вычисляли бы r Пирсона.

Рейтинг: Реализация SciPy

Вы можете использовать scipy.stats для определения ранга каждого значения в массиве. Сначала вы импортируете библиотеки и создадите массивы NumPy:

>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])

Теперь, когда вы подготовили данные, вы можете определить ранг каждого значения в массиве NumPy с помощью scipy.stats.rankdata():

>>> scipy.stats.rankdata(x)
array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])
>>> scipy.stats.rankdata(y)
array([ 2.,  1.,  3.,  4.,  5.,  6.,  7.,  8., 10.,  9.])
>>> scipy.stats.rankdata(z)
array([10.,  9.,  8.,  7.,  6.,  5.,  4.,  3.,  2.,  1.])

Массивы x и z монотонны, поэтому их ранги также монотонны. Наименьшее значение в y равно 1 и соответствует рангу 1. Вторым наименьшим значением является 2, что соответствует рангу 2. Наибольшее значение равно 96, что соответствует наибольшему рангу 10, поскольку в массиве 10 элементов.

rankdata() имеет необязательный параметр method. Он указывает Python, что делать, если в массиве есть связи (если два или более значений равны). По умолчанию он присваивает им среднее значение по рангам:

>>> scipy.stats.rankdata([8, 2, 0, 2])
array([4. , 2.5, 1. , 2.5])

Есть два элемента со значением 2, и они имеют ранги 2.0 и 3.0. Значение 0 имеет ранг 1.0, а значение 8 имеет ранг 4.0. Тогда оба элемента со значением 2 получат одинаковый ранг 2.5.

rankdata() обрабатывает значения nan так, как если бы они были большими:

>>> scipy.stats.rankdata([8, np.nan, 0, 2])
array([3., 4., 1., 2.])

В этом случае значение np.nan соответствует наибольшему рангу 4.0. Вы также можете получать звания с помощью np.argsort():

>>> np.argsort(y) + 1
array([ 2,  1,  3,  4,  5,  6,  7,  8, 10,  9])

argsort() возвращает индексы, которые были бы у элементов массива в отсортированном массиве. Эти индексы основаны на нуле, поэтому вам нужно будет добавить 1 ко всем из них.

Ранговая корреляция: реализация NumPy и SciPy

Вы можете рассчитать коэффициент корреляции Спирмена с помощью scipy.stats.spearmanr():

>>> result = scipy.stats.spearmanr(x, y)
>>> result
SpearmanrResult(correlation=0.9757575757575757, pvalue=1.4675461874042197e-06)
>>> result.correlation
0.9757575757575757
>>> result.pvalue
1.4675461874042197e-06
>>> rho, p = scipy.stats.spearmanr(x, y)
>>> rho
0.9757575757575757
>>> p
1.4675461874042197e-06

spearmanr() возвращает объект, содержащий значение коэффициента корреляции Спирмена и p-значение. Как вы можете видеть, вы можете получить доступ к определенным значениям двумя способами:

1. С использованием точечной записи (result.correlation и result.pvalue)
2. Распаковка с помощью Python (rho, p = scipy.stats.spearmanr(x, y))

Вы можете получить тот же результат, если введете двумерный массив xy, содержащий те же данные, что и x и y в spearmanr():

>>> xy = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
...                [2, 1, 4, 5, 8, 12, 18, 25, 96, 48]])
>>> rho, p = scipy.stats.spearmanr(xy, axis=1)
>>> rho
0.9757575757575757
>>> p
1.4675461874042197e-06

Первая строка xy - это один элемент, а вторая строка - другой элемент. Вы можете изменить это. Необязательный параметр axis определяет, будут ли столбцы (axis=0) или строки (axis=1) представлять объекты. По умолчанию строки являются наблюдениями, а столбцы - объектами.

Другой необязательный параметр nan_policy определяет, как обрабатывать значения nan. Он может принимать одно из трех значений:

• 'propagate' возвращает nan, если среди входных данных есть значение nan. Это поведение по умолчанию.
• 'raise' выдает значение ValueError, если среди входных данных есть значение nan.
• 'omit' игнорирует наблюдения со значениями nan.

Если вы предоставите двумерный массив с более чем двумя объектами, то получите корреляционную матрицу и матрицу p-значений:

>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
...                 [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
...                 [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])
>>> corr_matrix, p_matrix = scipy.stats.spearmanr(xyz, axis=1)
>>> corr_matrix
array([[ 1.        ,  0.97575758, -1.        ],
       [ 0.97575758,  1.        , -0.97575758],
       [-1.        , -0.97575758,  1.        ]])
>>> p_matrix
array([[6.64689742e-64, 1.46754619e-06, 6.64689742e-64],
       [1.46754619e-06, 6.64689742e-64, 1.46754619e-06],
       [6.64689742e-64, 1.46754619e-06, 6.64689742e-64]])

Значение -1 в корреляционной матрице показывает, что первый и третий признаки имеют идеальную отрицательную ранговую корреляцию, то есть большие значения в первой строке всегда соответствуют меньшим значениям в третьей.

Вы можете получить коэффициент корреляции Кендалла с помощью kendalltau():

>>> result = scipy.stats.kendalltau(x, y)
>>> result
KendalltauResult(correlation=0.911111111111111, pvalue=2.9761904761904762e-05)
>>> result.correlation
0.911111111111111
>>> result.pvalue
2.9761904761904762e-05
>>> tau, p = scipy.stats.kendalltau(x, y)
>>> tau
0.911111111111111
>>> p
2.9761904761904762e-05

kendalltau() работает во многом так же, как spearmanr(). Он принимает два одномерных массива, имеет необязательный параметр nan_policy и возвращает объект со значениями коэффициента корреляции и p-value.

Однако, если вы укажете в качестве аргумента только один двумерный массив, то kendalltau() вызовет TypeError. Если вы передадите два многомерных массива одинаковой формы, то перед вычислением они будут сглажены.

Ранговая корреляция: внедрение pandas

Вы можете рассчитать коэффициенты корреляции Спирмена и Кендалла с пандами. Как и раньше, вы начинаете с импорта pandas и создания нескольких экземпляров Series и DataFrame:

>>> import pandas as pd
>>> x, y, z = pd.Series(x), pd.Series(y), pd.Series(z)
>>> xy = pd.DataFrame({'x-values': x, 'y-values': y})
>>> xyz = pd.DataFrame({'x-values': x, 'y-values': y, 'z-values': z})

Теперь, когда у вас есть эти объекты pandas, вы можете использовать .corr() и .corrwith() точно так же, как вы это делали при вычислении коэффициента корреляции Пирсона. Вам просто нужно указать желаемый коэффициент корреляции с помощью необязательного параметра method, который по умолчанию равен 'pearson'.

Чтобы вычислить коэффициент Спирмена, передайте method=spearman:

>>> x.corr(y, method='spearman')
0.9757575757575757
>>> xy.corr(method='spearman')
          x-values  y-values
x-values  1.000000  0.975758
y-values  0.975758  1.000000
>>> xyz.corr(method='spearman')
          x-values  y-values  z-values
x-values  1.000000  0.975758 -1.000000
y-values  0.975758  1.000000 -0.975758
z-values -1.000000 -0.975758  1.000000
>>> xy.corrwith(z, method='spearman')
x-values   -1.000000
y-values   -0.975758
dtype: float64

Если вам нужен тау Кендалла, то вы используете method=kendall:

>>> x.corr(y, method='kendall')
0.911111111111111
>>> xy.corr(method='kendall')
          x-values  y-values
x-values  1.000000  0.911111
y-values  0.911111  1.000000
>>> xyz.corr(method='kendall')
          x-values  y-values  z-values
x-values  1.000000  0.911111 -1.000000
y-values  0.911111  1.000000 -0.911111
z-values -1.000000 -0.911111  1.000000
>>> xy.corrwith(z, method='kendall')
x-values   -1.000000
y-values   -0.911111
dtype: float64

Как вы можете видеть, в отличие от SciPy, вы можете использовать единую двумерную структуру данных (фрейм данных).

Визуализация корреляции

Визуализация данных очень важна в статистике и науке о данных. Она может помочь вам лучше понять ваши данные и лучше понять взаимосвязи между объектами. В этом разделе вы узнаете, как визуально представить взаимосвязь между двумя объектами с помощью графика x-y. Вы также будете использовать тепловые карты для визуализации корреляционной матрицы.

Вы узнаете, как подготавливать данные и получать определенные визуальные представления, но не получите многих других объяснений. Чтобы узнать больше о Matplotlib в деталях, ознакомьтесь с Построение графиков на Python с помощью Matplotlib (руководство). Вы также можете ознакомиться с официальной документацией и Анатомией Matplotlib.

Чтобы начать, сначала выполните импорт matplotlib.pyplot:

>>> import matplotlib.pyplot as plt
>>> plt.style.use('ggplot')

Здесь вы используете plt.style.use('ggplot'), чтобы задать стиль графиков. Если хотите, можете пропустить эту строку.

Вы будете использовать массивы x, y, z, и xyz из предыдущих разделов. Вы можете создать их снова, чтобы сократить время прокрутки:

>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
...                 [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
...                 [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])

Теперь, когда у вас есть необходимые данные, вы готовы к построению графика.

Графики X-Y С линией регрессии

Сначала вы увидите, как построить график x-y с линией регрессии, ее уравнением и коэффициентом корреляции Пирсона. Вы можете получить наклон и пересечение линии регрессии, а также коэффициент корреляции с помощью linregress():

>>> slope, intercept, r, p, stderr = scipy.stats.linregress(x, y)

Теперь у вас есть все необходимые значения. Вы также можете получить строку с уравнением линии регрессии и значением коэффициента корреляции. f-строки очень удобны для этой цели:

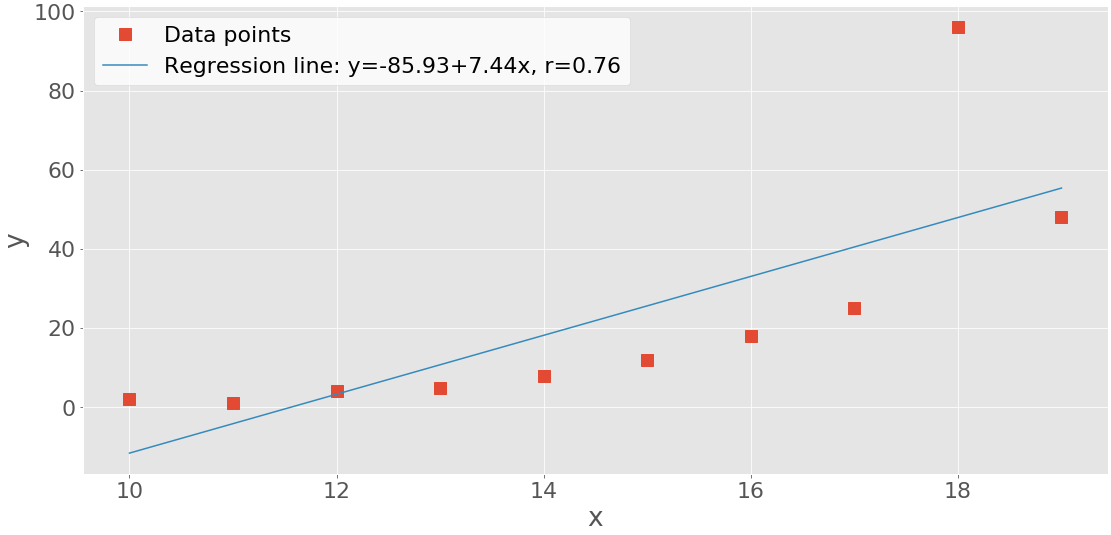
>>> line = f'Regression line: y={intercept:.2f}+{slope:.2f}x, r={r:.2f}'
>>> line
'Regression line: y=-85.93+7.44x, r=0.76'

Теперь создайте график x-y с помощью .plot():

fig, ax = plt.subplots()
ax.plot(x, y, linewidth=0, marker='s', label='Data points')
ax.plot(x, intercept + slope * x, label=line)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(facecolor='white')
plt.show()

Ваши выходные данные должны выглядеть следующим образом:

Красные квадраты представляют результаты наблюдений, а синяя линия - линию регрессии. В условных обозначениях приведено ее уравнение вместе с коэффициентом корреляции.

Тепловые карты корреляционных матриц

Корреляционная матрица может стать действительно большой и запутанной, если у вас много функций! К счастью, вы можете представить ее визуально в виде тепловой карты, где каждое поле имеет цвет, соответствующий его значению. Вам понадобится корреляционная матрица:

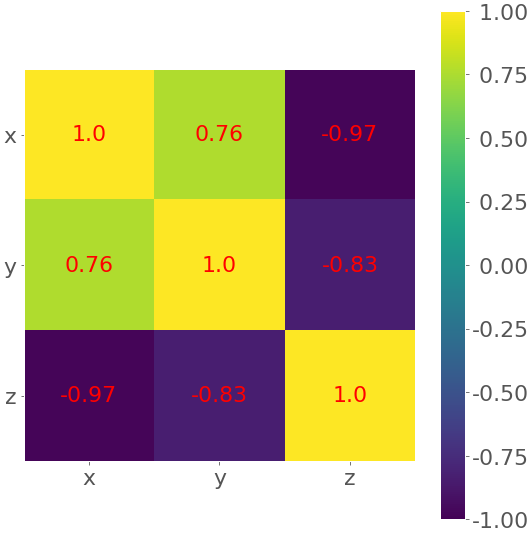
>>> corr_matrix = np.corrcoef(xyz).round(decimals=2)
>>> corr_matrix
array([[ 1.  ,  0.76, -0.97],
       [ 0.76,  1.  , -0.83],
       [-0.97, -0.83,  1.  ]])

Возможно, вам будет удобно округлить числа в корреляционной матрице на величину .round(),, поскольку они будут отображаться на тепловой карте.

Наконец, создайте свою тепловую карту, используя .imshow() и корреляционную матрицу в качестве аргумента:

fig, ax = plt.subplots()
im = ax.imshow(corr_matrix)
im.set_clim(-1, 1)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1, 2), ticklabels=('x', 'y', 'z'))
ax.yaxis.set(ticks=(0, 1, 2), ticklabels=('x', 'y', 'z'))
ax.set_ylim(2.5, -0.5)
for i in range(3):
    for j in range(3):
        ax.text(j, i, corr_matrix[i, j], ha='center', va='center',
                color='r')
cbar = ax.figure.colorbar(im, ax=ax, format='% .2f')
plt.show()

Ваши выходные данные должны выглядеть следующим образом:

Результатом является таблица с коэффициентами. Это похоже на вывод pandas с цветным фоном. Цвета помогают интерпретировать вывод. В этом примере желтый цвет обозначает число 1, зеленый соответствует 0,76, а фиолетовый используется для отрицательных чисел.

Заключение

Теперь вы знаете, что коэффициенты корреляции - это статистические данные, которые измеряют связь между переменными или характеристиками наборов данных. Они очень важны в науке о данных и машинном обучении.

Теперь вы можете использовать Python для вычисления:

• Коэффициент корреляции между продуктом и моментом Пирсона
• Коэффициент ранговой корреляции Спирмена
• Коэффициент ранговой корреляции Кендалла

Теперь вы можете использовать корреляционные функции и методы NumPy, SciPy и pandas для эффективного расчета этих (и других) статистических данных даже при работе с большими наборами данных. Вы также знаете, как визуализировать данные, линии регрессии и корреляционные матрицы с помощью графиков Matplotlib и тепловых карт.

Если у вас есть какие-либо вопросы или комментарии, пожалуйста, задавайте их в разделе комментариев ниже!

Back to Top