Множества в Python

Оглавление

• Определение множества
• Размер и принадлежность множества
• Операции над множеством
  • Операторы против методов
  • Доступные операторы и методы
• Модификация множества
  • Операторы и методы дополненного присваивания
  • Другие методы модификации множеств
• Замороженные наборы
• Заключение

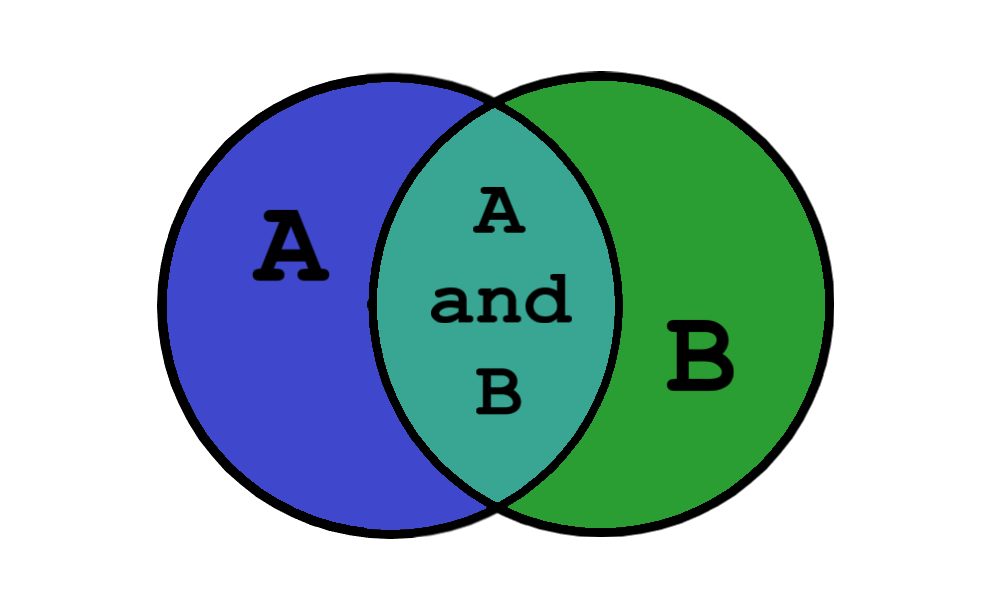
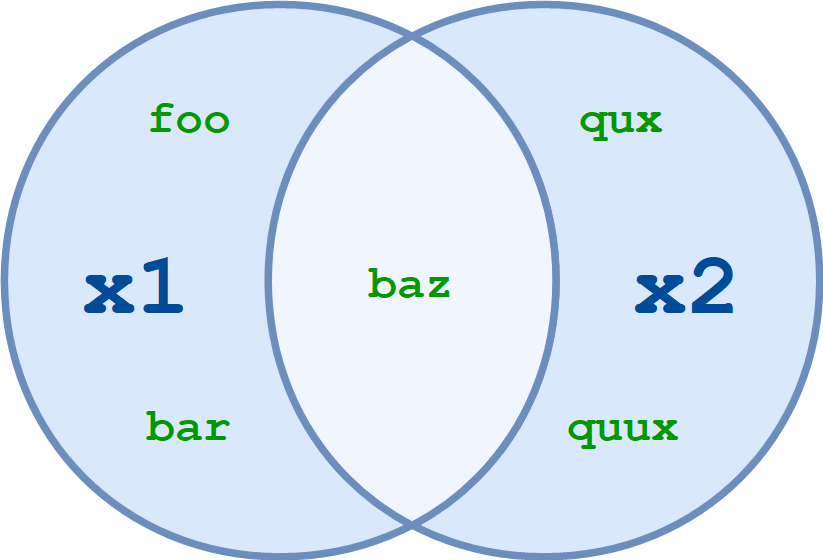
Возможно, вы помните, как на каком-то этапе вашего математического образования вы узнали о множествах и теории множеств. Возможно, вы даже помните диаграммы Венна:

Если вам это ничего не напоминает, не волнуйтесь! Этот учебник по-прежнему должен быть легко доступен для вас.

В математике строгое определение множества может быть абстрактным и сложным для понимания. Однако на практике о множестве можно думать просто как о вполне определенной коллекции отдельных объектов, обычно называемых элементами или членами.

Группировка объектов в набор может быть полезна и в программировании, и Python предоставляет для этого встроенный тип набора. Наборы отличаются от других типов объектов уникальными операциями, которые можно выполнять над ними.

Вот что вы узнаете из этого урока: Вы увидите, как определять объекты set в Python, и познакомитесь с операциями, которые они поддерживают. Как и в предыдущих уроках по спискам и словарям, по завершении этого урока вы должны хорошо понимать, когда набор является подходящим выбором. Вы также узнаете о замороженных множествах, которые похожи на множества за исключением одной важной детали.

Определение множества

Встроенный тип set в Python имеет следующие характеристики:

• Наборы неупорядочены.
• Элементы набора уникальны. Дублирование элементов не допускается.
• Само множество может быть изменено, но элементы, содержащиеся в нем, должны быть неизменяемого типа.

Давайте посмотрим, что все это значит и как можно работать с множествами в Python.

Набор может быть создан двумя способами. Во-первых, можно определить набор с помощью встроенной функции set():

x = set(<iter>)

В этом случае аргумент <iter> представляет собой итерируемую переменную - опять же, пока что думайте о списке или кортеже, - которая формирует список объектов, включаемых в набор. Это аналогично аргументу <iter>, передаваемому методу .extend() list:

>>> x = set(['foo', 'bar', 'baz', 'foo', 'qux'])
>>> x
{'qux', 'foo', 'bar', 'baz'}

>>> x = set(('foo', 'bar', 'baz', 'foo', 'qux'))
>>> x
{'qux', 'foo', 'bar', 'baz'}

Строки также итерируемы, поэтому строка может быть передана и в set(). Вы уже видели, что list(s) генерирует список символов в строке s. Аналогично, set(s) генерирует набор символов в строке s:

>>> s = 'quux'

>>> list(s)
['q', 'u', 'u', 'x']
>>> set(s)
{'x', 'u', 'q'}

Вы видите, что полученные множества неупорядочены: исходный порядок, указанный в определении, не обязательно сохраняется. Кроме того, дублирующиеся значения представлены в наборе только один раз, как в случае со строкой 'foo' в первых двух примерах и буквой 'u' в третьем.

Альтернативно, множество можно определить с помощью фигурных скобок ({}):

x = {<obj>, <obj>, ..., <obj>}

<<<Когда множество определено таким образом, каждый

становится <obj> отдельным элементом множества, даже если это итерируемый элемент. Это поведение аналогично поведению метода .append() списка.

Таким образом, приведенные выше множества можно определить следующим образом:

>>> x = {'foo', 'bar', 'baz', 'foo', 'qux'}
>>> x
{'qux', 'foo', 'bar', 'baz'}

>>> x = {'q', 'u', 'u', 'x'}
>>> x
{'x', 'q', 'u'}

Вкратце:

• Аргументом к set() является итерируемая переменная. Он генерирует список элементов, которые должны быть помещены в множество.
• Объекты в фигурных скобках помещаются в набор нетронутыми, даже если они являются итерируемыми.

Обратите внимание на разницу между этими двумя определениями множеств:

>>> {'foo'}
{'foo'}

>>> set('foo')
{'o', 'f'}

Множество может быть пустым. Однако вспомните, что Python интерпретирует пустые фигурные скобки ({}) как пустой словарь, поэтому единственный способ определить пустое множество - это функция set():

>>> x = set()
>>> type(x)
<class 'set'>
>>> x
set()

>>> x = {}
>>> type(x)
<class 'dict'>

Пустое множество является ложным в булевом контексте:

>>> x = set()
>>> bool(x)
False
>>> x or 1
1
>>> x and 1
set()

Вы можете подумать, что наиболее интуитивно понятные наборы будут содержать похожие объекты - например, даже числа или фамилии:

>>> s1 = {2, 4, 6, 8, 10}
>>> s2 = {'Smith', 'McArthur', 'Wilson', 'Johansson'}

Однако

Python этого не требует. Элементы множества могут быть объектами разных типов:

>>> x = {42, 'foo', 3.14159, None}
>>> x
{None, 'foo', 42, 3.14159}

Не забывайте, что элементы набора должны быть неизменяемыми. Например, кортеж может быть включен в набор:

>>> x = {42, 'foo', (1, 2, 3), 3.14159}
>>> x
{42, 'foo', 3.14159, (1, 2, 3)}

Но списки и словари мутабельны, поэтому они не могут быть элементами множества:

>>> a = [1, 2, 3]
>>> {a}
Traceback (most recent call last):
  File "<pyshell#70>", line 1, in <module>
    {a}
TypeError: unhashable type: 'list'

>>> d = {'a': 1, 'b': 2}
>>> {d}
Traceback (most recent call last):
  File "<pyshell#72>", line 1, in <module>
    {d}
TypeError: unhashable type: 'dict'

Установить размер и членство

Функция len() возвращает количество элементов в множестве, а операторы in и not in можно использовать для проверки принадлежности:

>>> x = {'foo', 'bar', 'baz'}

>>> len(x)
3

>>> 'bar' in x
True
>>> 'qux' in x
False

Оперирование множеством

Многие операции, которые можно использовать для других составных типов данных Python, не имеют смысла для множеств. Например, множества нельзя индексировать или разрезать. Однако Python предоставляет целый ряд операций над объектами множеств, которые в целом имитируют операции, определенные для математических множеств.

Операторы против методов

Большинство, хотя и не совсем все, операции с множествами в Python можно выполнять двумя разными способами: оператором или методом. Давайте рассмотрим, как работают эти операторы и методы, на примере объединения множеств.

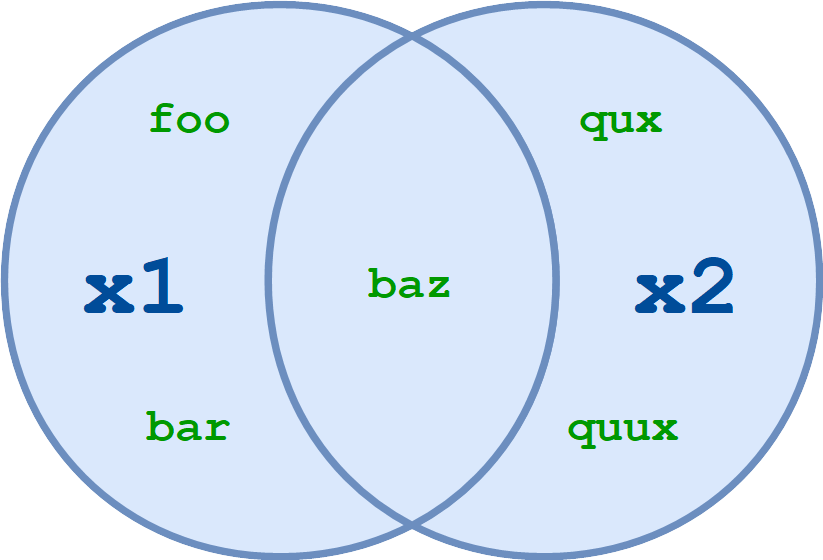
Для двух множеств, x1 и x2, объединение x1 и x2 - это множество, состоящее из всех элементов любого из этих множеств.

Рассмотрим эти два набора:

x1 = {'foo', 'bar', 'baz'}
x2 = {'baz', 'qux', 'quux'}

Объединение x1 и x2 равно {'foo', 'bar', 'baz', 'qux', 'quux'}.

Примечание: Обратите внимание, что элемент 'baz', который встречается и в x1, и в x2, появляется в объединении только один раз. Наборы никогда не содержат дублирующихся значений.

В Python объединение множеств можно выполнить с помощью оператора |:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'baz', 'qux', 'quux'}
>>> x1 | x2
{'baz', 'quux', 'qux', 'bar', 'foo'}

Объединение множеств можно также получить с помощью метода .union(). Метод вызывается на одном из множеств, а второе передается в качестве аргумента:

>>> x1.union(x2)
{'baz', 'quux', 'qux', 'bar', 'foo'}

При использовании их в приведенных примерах оператор и метод ведут себя одинаково. Однако между ними есть тонкое различие. Когда вы используете оператор |, оба операнда должны быть множествами. Метод .union(), напротив, принимает в качестве аргумента любую итерируемую переменную, преобразует ее в множество, а затем выполняет объединение.

Обратите внимание на разницу между этими двумя утверждениями:

>>> x1 | ('baz', 'qux', 'quux')
Traceback (most recent call last):
  File "<pyshell#43>", line 1, in <module>
    x1 | ('baz', 'qux', 'quux')
TypeError: unsupported operand type(s) for |: 'set' and 'tuple'

>>> x1.union(('baz', 'qux', 'quux'))
{'baz', 'quux', 'qux', 'bar', 'foo'}

Оба пытаются вычислить объединение x1 и кортежа ('baz', 'qux', 'quux'). Это не удается с помощью оператора |, но удается с помощью метода .union().

Доступные операторы и методы

Ниже приведен список операций над множествами, доступных в Python. Некоторые из них выполняются оператором, некоторые - методом, а некоторые - обоими способами. В общем случае действует принцип, описанный выше: если ожидается множество, методы обычно принимают в качестве аргумента любой итерируемый объект, а операторы требуют в качестве операндов реальные множества.

x1.union(x2[, x3 ...])

x1 | x2 [| x3 ...]

Вычислите объединение двух или более множеств.

x1.union(x2) и x1 | x2 оба возвращают множество всех элементов в x1 или x2:

 

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'baz', 'qux', 'quux'}

>>> x1.union(x2)
{'foo', 'qux', 'quux', 'baz', 'bar'}

>>> x1 | x2
{'foo', 'qux', 'quux', 'baz', 'bar'}

С помощью оператора или метода можно указать более двух наборов:

>>> a = {1, 2, 3, 4}
>>> b = {2, 3, 4, 5}
>>> c = {3, 4, 5, 6}
>>> d = {4, 5, 6, 7}

>>> a.union(b, c, d)
{1, 2, 3, 4, 5, 6, 7}

>>> a | b | c | d
{1, 2, 3, 4, 5, 6, 7}

Результирующее множество содержит все элементы, которые присутствуют в любом из указанных множеств.

x1.intersection(x2[, x3 ...])

x1 & x2 [& x3 ...]

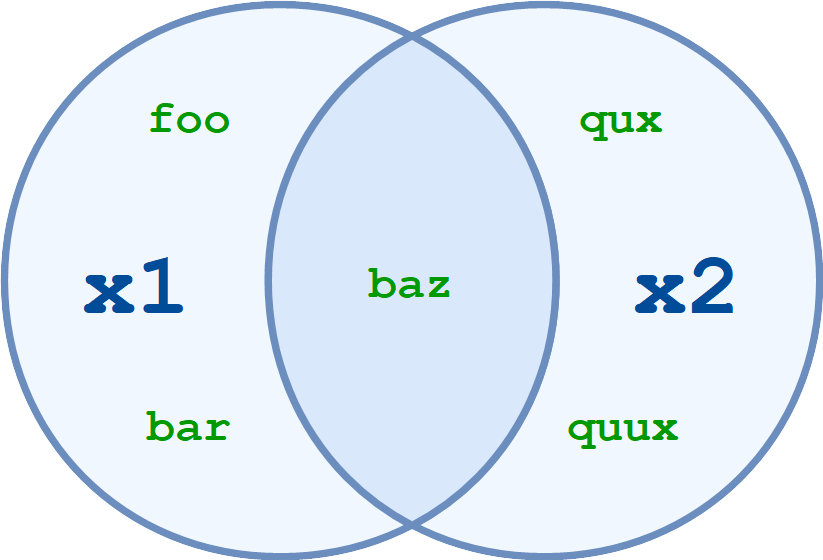
Вычислите пересечение двух или более множеств.

x1.intersection(x2) и x1 & x2 возвращают множество элементов, общих для x1 и x2:

 

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'baz', 'qux', 'quux'}

>>> x1.intersection(x2)
{'baz'}

>>> x1 & x2
{'baz'}

С помощью метода и оператора intersection можно указать несколько множеств, как и в случае с объединением множеств:

>>> a = {1, 2, 3, 4}
>>> b = {2, 3, 4, 5}
>>> c = {3, 4, 5, 6}
>>> d = {4, 5, 6, 7}

>>> a.intersection(b, c, d)
{4}

>>> a & b & c & d
{4}

Результирующее множество содержит только те элементы, которые присутствуют во всех указанных множествах.

x1.difference(x2[, x3 ...])

x1 - x2 [- x3 ...]

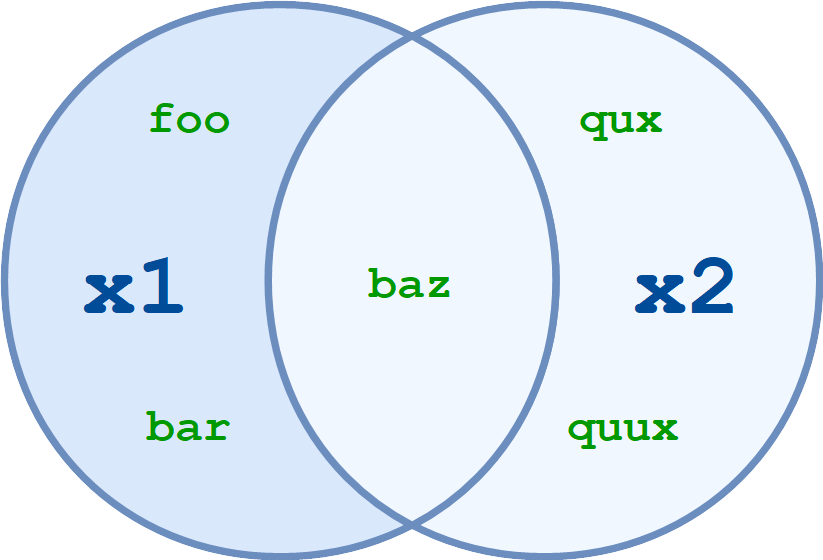
Вычислите разность между двумя или более множествами.

x1.difference(x2) и x1 - x2 возвращают множество всех элементов, которые находятся в x1, но не в x2:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'baz', 'qux', 'quux'}

>>> x1.difference(x2)
{'foo', 'bar'}

>>> x1 - x2
{'foo', 'bar'}

Другой способ представить это так: x1.difference(x2) и x1 - x2 возвращают множество, которое получается, когда любые элементы из x2 удаляются или вычитаются из x1.

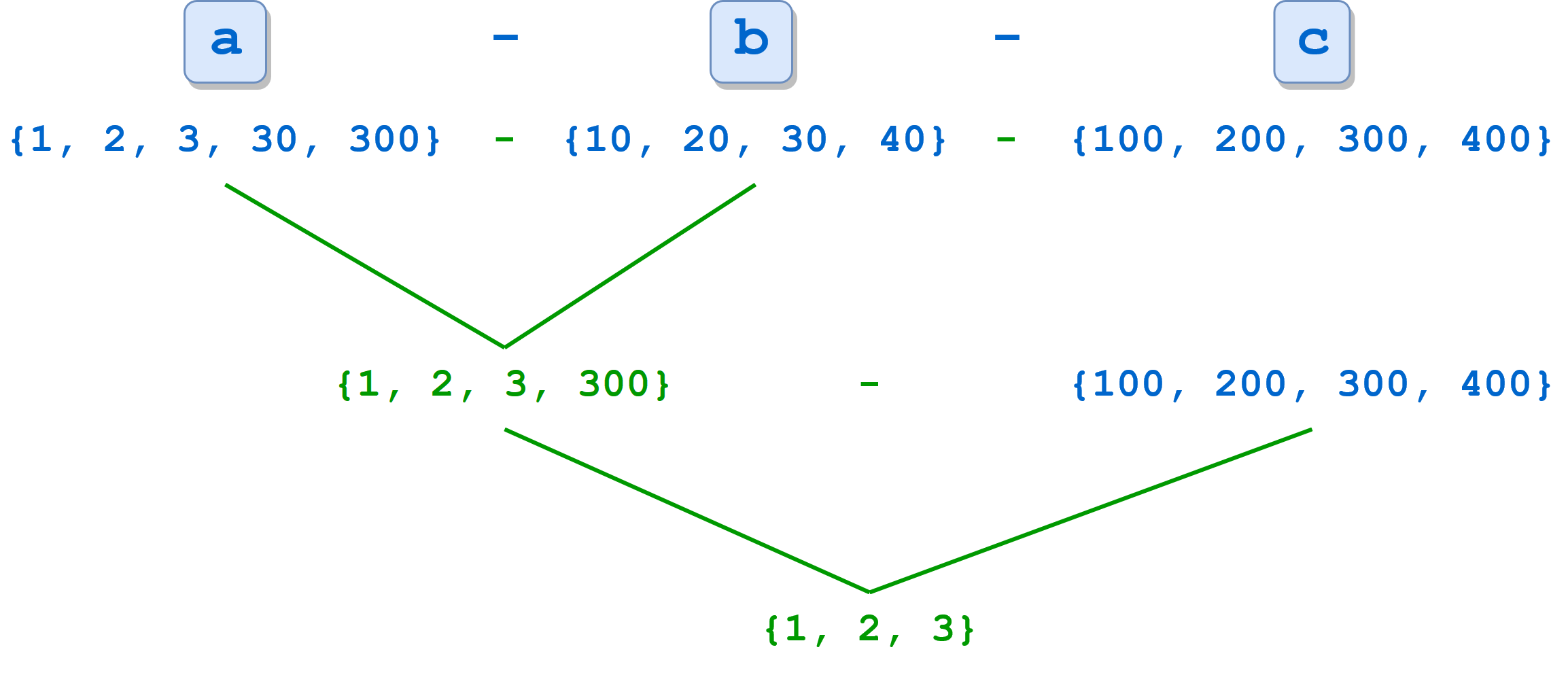
Опять же, можно указать более двух наборов:

>>> a = {1, 2, 3, 30, 300}
>>> b = {10, 20, 30, 40}
>>> c = {100, 200, 300, 400}

>>> a.difference(b, c)
{1, 2, 3}

>>> a - b - c
{1, 2, 3}

Если указано несколько наборов, операция выполняется слева направо. В приведенном выше примере сначала вычисляется a - b, в результате чего получается {1, 2, 3, 300}. Затем из этого набора вычитается c, в результате чего остается {1, 2, 3}:

x1.symmetric_difference(x2)

x1 ^ x2 [^ x3 ...]

Вычислите симметричную разность между множествами.

x1.symmetric_difference(x2) и x1 ^ x2 возвращают множество всех элементов в x1 или x2, но не в обоих:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'baz', 'qux', 'quux'}

>>> x1.symmetric_difference(x2)
{'foo', 'qux', 'quux', 'bar'}

>>> x1 ^ x2
{'foo', 'qux', 'quux', 'bar'}

Оператор ^ также позволяет использовать более двух наборов:

>>> a = {1, 2, 3, 4, 5}
>>> b = {10, 2, 3, 4, 50}
>>> c = {1, 50, 100}

>>> a ^ b ^ c
{100, 5, 10}

Как и в случае с оператором разности, если указано несколько множеств, операция выполняется слева направо.

Любопытно, что хотя оператор ^ позволяет использовать несколько множеств, метод .symmetric_difference() этого не делает:

>>> a = {1, 2, 3, 4, 5}
>>> b = {10, 2, 3, 4, 50}
>>> c = {1, 50, 100}

>>> a.symmetric_difference(b, c)
Traceback (most recent call last):
  File "<pyshell#11>", line 1, in <module>
    a.symmetric_difference(b, c)
TypeError: symmetric_difference() takes exactly one argument (2 given)

x1.isdisjoint(x2)

Определяет, есть ли у двух множеств общие элементы.

x1.isdisjoint(x2) возвращает True, если x1 и x2 не имеют общих элементов:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'baz', 'qux', 'quux'}

>>> x1.isdisjoint(x2)
False

>>> x2 - {'baz'}
{'quux', 'qux'}
>>> x1.isdisjoint(x2 - {'baz'})
True

Если x1.isdisjoint(x2) является True, то x1 & x2 является пустым множеством:

>>> x1 = {1, 3, 5}
>>> x2 = {2, 4, 6}

>>> x1.isdisjoint(x2)
True
>>> x1 & x2
set()

Примечание: Не существует оператора, соответствующего методу .isdisjoint().

x1.issubset(x2)

x1 <= x2

Определите, является ли одно множество подмножеством другого.

В теории множеств множество x1 считается подмножеством другого множества x2, если каждый элемент x1 находится в x2.

x1.issubset(x2) и x1 <= x2 возвращают True, если x1 является подмножеством x2:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x1.issubset({'foo', 'bar', 'baz', 'qux', 'quux'})
True

>>> x2 = {'baz', 'qux', 'quux'}
>>> x1 <= x2
False

Множество считается подмножеством самого себя:

>>> x = {1, 2, 3, 4, 5}
>>> x.issubset(x)
True
>>> x <= x
True

Это кажется странным, возможно. Но это соответствует определению - каждый элемент x находится в x.

x1 < x2

Определяет, является ли одно множество правильным подмножеством другого.

Правильное подмножество - это то же самое, что и подмножество, за исключением того, что множества не могут быть одинаковыми. Множество x1 считается правильным подмножеством другого множества x2, если каждый элемент x1 находится в x2, а x1 и x2 не равны.

x1 < x2 возвращает True, если x1 является правильным подмножеством x2:

>>> x1 = {'foo', 'bar'}
>>> x2 = {'foo', 'bar', 'baz'}
>>> x1 < x2
True

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'foo', 'bar', 'baz'}
>>> x1 < x2
False

Хотя множество считается подмножеством самого себя, оно не является собственным подмножеством самого себя:

>>> x = {1, 2, 3, 4, 5}
>>> x <= x
True
>>> x < x
False

Примечание: Оператор < является единственным способом проверки того, является ли множество правильным подмножеством. Соответствующего метода не существует.

x1.issuperset(x2)

x1 >= x2

Определите, является ли одно множество надмножеством другого.

Надмножество - это подмножество, обратное подмножеству. Множество x1 считается супермножеством другого множества x2, если x1 содержит каждый элемент x2.

x1.issuperset(x2) и x1 >= x2 возвращают True, если x1 является надмножеством x2:

>>> x1 = {'foo', 'bar', 'baz'}

>>> x1.issuperset({'foo', 'bar'})
True

>>> x2 = {'baz', 'qux', 'quux'}
>>> x1 >= x2
False

Вы уже видели, что множество считается подмножеством самого себя. Множество также считается надмножеством самого себя:

>>> x = {1, 2, 3, 4, 5}
>>> x.issuperset(x)
True
>>> x >= x
True

x1 > x2

Определяет, является ли одно множество правильным супермножеством другого.

Правильный супернабор - это то же самое, что и супернабор, за исключением того, что наборы не могут быть одинаковыми. Множество x1 считается правильным супермножеством другого множества x2, если x1 содержит каждый элемент x2, а x1 и x2 не равны.

x1 > x2 возвращает True, если x1 является правильным супермножеством x2:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'foo', 'bar'}
>>> x1 > x2
True

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'foo', 'bar', 'baz'}
>>> x1 > x2
False

Множество не является правильным супермножеством самого себя:

>>> x = {1, 2, 3, 4, 5}
>>> x > x
False

Примечание: Оператор > является единственным способом проверить, является ли множество правильным супермножеством. Соответствующего метода не существует.

Модификация набора

Хотя элементы, содержащиеся в множестве, должны быть неизменяемого типа, сами множества могут быть изменены. Как и в случае с операциями, описанными выше, существует множество операторов и методов, которые можно использовать для изменения содержимого множества.

Операторы и методы дополненного присваивания

Каждый из перечисленных выше операторов объединения, пересечения, разности и симметричной разности имеет форму дополненного назначения, которая может быть использована для изменения множества. Для каждого из них также существует соответствующий метод.

x1.update(x2[, x3 ...])

x1 |= x2 [| x3 ...]

Модификация множества путем объединения.

x1.update(x2) и x1 |= x2 добавляют к x1 любые элементы в x2, которых еще нет в x1:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'foo', 'baz', 'qux'}

>>> x1 |= x2
>>> x1
{'qux', 'foo', 'bar', 'baz'}

>>> x1.update(['corge', 'garply'])
>>> x1
{'qux', 'corge', 'garply', 'foo', 'bar', 'baz'}

x1.intersection_update(x2[, x3 ...])

x1 &= x2 [& x3 ...]

Модификация множества путем пересечения.

x1.intersection_update(x2) и x1 &= x2 обновляют x1, сохраняя только элементы, встречающиеся в x1 и x2:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'foo', 'baz', 'qux'}

>>> x1 &= x2
>>> x1
{'foo', 'baz'}

>>> x1.intersection_update(['baz', 'qux'])
>>> x1
{'baz'}

x1.difference_update(x2[, x3 ...])

x1 -= x2 [| x3 ...]

Модификация набора по разности.

x1.difference_update(x2) и x1 -= x2 обновляют x1, удаляя элементы, найденные в x2:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'foo', 'baz', 'qux'}

>>> x1 -= x2
>>> x1
{'bar'}

>>> x1.difference_update(['foo', 'bar', 'qux'])
>>> x1
set()

x1.symmetric_difference_update(x2)

x1 ^= x2

Модификация множества с помощью симметричной разности.

x1.symmetric_difference_update(x2) и x1 ^= x2 обновляют x1, сохраняя элементы, найденные либо в x1, либо в x2, но не в обоих:

>>> x1 = {'foo', 'bar', 'baz'}
>>> x2 = {'foo', 'baz', 'qux'}
>>> 
>>> x1 ^= x2
>>> x1
{'bar', 'qux'}
>>> 
>>> x1.symmetric_difference_update(['qux', 'corge'])
>>> x1
{'bar', 'corge'}

Другие методы изменения множеств

Помимо вышеперечисленных дополненных операторов, Python поддерживает несколько дополнительных методов, которые изменяют множества.

x.add(<elem>)

Добавляет элемент к множеству.

x.add(<elem>) добавляет <elem>, который должен быть одним неизменяемым объектом, к x:

>>> x = {'foo', 'bar', 'baz'}

>>> x.add('qux')
>>> x
{'bar', 'baz', 'foo', 'qux'}

x.remove(<elem>)

Удаляет элемент из множества.

x.remove(<elem>) удаляет <elem> из x. Python вызывает исключение, если <elem> не находится в x:

>>> x = {'foo', 'bar', 'baz'}

>>> x.remove('baz')
>>> x
{'bar', 'foo'}

>>> x.remove('qux')
Traceback (most recent call last):
  File "<pyshell#58>", line 1, in <module>
    x.remove('qux')
KeyError: 'qux'

x.discard(<elem>)

Удаляет элемент из множества.

x.discard(<elem>) также удаляет <elem> из x. Однако, если <elem> не находится в x, этот метод ничего не делает, вместо того чтобы вызвать исключение:

>>> x = {'foo', 'bar', 'baz'}

>>> x.discard('baz')
>>> x
{'bar', 'foo'}

>>> x.discard('qux')
>>> x
{'bar', 'foo'}

x.pop()

Удаляет случайный элемент из множества.

x.pop() удаляет и возвращает произвольно выбранный элемент из x. Если x пуст, x.pop() вызывает исключение:

>>> x = {'foo', 'bar', 'baz'}

>>> x.pop()
'bar'
>>> x
{'baz', 'foo'}

>>> x.pop()
'baz'
>>> x
{'foo'}

>>> x.pop()
'foo'
>>> x
set()

>>> x.pop()
Traceback (most recent call last):
  File "<pyshell#82>", line 1, in <module>
    x.pop()
KeyError: 'pop from an empty set'

x.clear()

Очищает набор.

x.clear() удаляет все элементы из x:

>>> x = {'foo', 'bar', 'baz'}
>>> x
{'foo', 'bar', 'baz'}
>>> 
>>> x.clear()
>>> x
set()

Замороженные наборы

Python предоставляет еще один встроенный тип, называемый frozenset, который во всех отношениях похож на множество, за исключением того, что frozenset является неизменяемым. Вы можете выполнять немодифицирующие операции над frozenset:

>>> x = frozenset(['foo', 'bar', 'baz'])
>>> x
frozenset({'foo', 'baz', 'bar'})

>>> len(x)
3

>>> x & {'baz', 'qux', 'quux'}
frozenset({'baz'})

Но методы, которые пытаются изменить фростенсет, терпят неудачу:

>>> x = frozenset(['foo', 'bar', 'baz'])

>>> x.add('qux')
Traceback (most recent call last):
  File "<pyshell#127>", line 1, in <module>
    x.add('qux')
AttributeError: 'frozenset' object has no attribute 'add'

>>> x.pop()
Traceback (most recent call last):
  File "<pyshell#129>", line 1, in <module>
    x.pop()
AttributeError: 'frozenset' object has no attribute 'pop'

>>> x.clear()
Traceback (most recent call last):
  File "<pyshell#131>", line 1, in <module>
    x.clear()
AttributeError: 'frozenset' object has no attribute 'clear'

>>> x
frozenset({'foo', 'bar', 'baz'})

Глубокое погружение: Фростенсеты и дополненное присваивание

Поскольку фростенсет неизменяем, вы можете подумать, что он не может быть целью оператора дополненного присваивания. Но обратите внимание:

>>> f = frozenset(['foo', 'bar', 'baz'])
>>> s = {'baz', 'qux', 'quux'}

>>> f &= s
>>> f
frozenset({'baz'})

Что же получается?

Python не выполняет дополненные присваивания на frozensets in place. Утверждение x &= s фактически эквивалентно x = x & s. Оно не изменяет исходное x. Оно переназначает x новому объекту, а объект , на который первоначально ссылался x, исчезает.

Вы можете проверить это с помощью функции id():

>>> f = frozenset(['foo', 'bar', 'baz'])
>>> id(f)
56992872
>>> s = {'baz', 'qux', 'quux'}

>>> f &= s
>>> f
frozenset({'baz'})
>>> id(f)
56992152

f после дополненного присваивания имеет другой целочисленный идентификатор. Он был переназначен, а не изменен на месте.

Некоторые объекты в Python модифицируются на месте, когда они являются целью оператора дополненного присваивания. Но фростенсеты - нет.

Фростенсеты полезны в ситуациях, когда вы хотите использовать набор, но вам нужен неизменяемый объект. Например, вы не можете определить множество, элементы которого также являются множествами, поскольку элементы множества должны быть неизменяемыми:

>>> x1 = set(['foo'])
>>> x2 = set(['bar'])
>>> x3 = set(['baz'])
>>> x = {x1, x2, x3}
Traceback (most recent call last):
  File "<pyshell#38>", line 1, in <module>
    x = {x1, x2, x3}
TypeError: unhashable type: 'set'

Если вы действительно чувствуете себя вынужденным определить набор множеств (эй, это может случиться), вы можете сделать это, если элементы являются frozensets, потому что они неизменяемы:

>>> x1 = frozenset(['foo'])
>>> x2 = frozenset(['bar'])
>>> x3 = frozenset(['baz'])
>>> x = {x1, x2, x3}
>>> x
{frozenset({'bar'}), frozenset({'baz'}), frozenset({'foo'})}

Аналогично, вспомните из предыдущего урока по словарям, что ключ словаря должен быть неизменяемым. Вы не можете использовать встроенный тип set в качестве ключа словаря:

>>> x = {1, 2, 3}
>>> y = {'a', 'b', 'c'}
>>> 
>>> d = {x: 'foo', y: 'bar'}
Traceback (most recent call last):
  File "<pyshell#3>", line 1, in <module>
    d = {x: 'foo', y: 'bar'}
TypeError: unhashable type: 'set'

Если вам понадобится использовать наборы в качестве ключей словаря, вы можете использовать frozensets:

>>> x = frozenset({1, 2, 3})
>>> y = frozenset({'a', 'b', 'c'})
>>> 
>>> d = {x: 'foo', y: 'bar'}
>>> d
{frozenset({1, 2, 3}): 'foo', frozenset({'c', 'a', 'b'}): 'bar'}

Заключение

В этом уроке вы узнали, как определять объекты set в Python, и познакомились с функциями, операторами и методами, которые можно использовать для работы с множествами.

Теперь вы должны хорошо ориентироваться в основных встроенных типах данных, которые предоставляет Python.

Далее вы начнете изучать, как организован и структурирован код, работающий с этими объектами, в программе на Python.

Back to Top