Логистическая регрессия в Python

Оглавление

• Классификация
  • Что такое Классификация?
  • Когда Вам Нужна Классификация?
• Обзор логистической регрессии
  • Математические предпосылки
  • Формулировка задачи
  • Методология
  • Эффективность классификации
  • Логистическая регрессия с одной переменной
  • Многовариантная логистическая регрессия
  • Регуляризация
• Логистическая регрессия в Python
  • Пакеты Python для логистической регрессии
  • Логистическая регрессия на Python с помощью scikit-learn: Пример 1
  • Логистическая регрессия на Python с помощью scikit-learn: Пример 2
  • Логистическая регрессия в Python с использованием StatsModels: Пример
  • Логистическая регрессия в Python: распознавание рукописного ввода
• За пределами логистической регрессии в Python
• Заключение

Так как сумма имеющихся данных, прочность вычислительной мощности, и ряд алгоритмических улучшений продолжают расти, на первый план выходит важность данные науки и машинного обучения. классификация является одним из важнейших направлений машинного обучения, а также логистическая регрессия является одним из ее основных методов. К концу этого урока вы узнаете о классификации в целом и основах логистической регрессии в частности, а также о том, как реализовать логистическую регрессию в Python.

В этом уроке вы узнаете:

• Что такое логистическая регрессия
• Для чего используется логистическая регрессия
• Как работает логистическая регрессия
• Как реализовать логистическую регрессию на Python, шаг за шагом

Классификация

Классификация является очень важной областью машинного обучения с контролем. Большое количество важных проблем машинного обучения относится к этой области. Существует множество методов классификации, и логистическая регрессия является одним из них.

Что такое классификация?

Алгоритмы контролируемого машинного обучения определяют модели, которые фиксируют взаимосвязи между данными. Классификация - это область контролируемого машинного обучения, которая пытается предсказать, к какому классу или категории относится тот или иной объект, основываясь на его характеристиках.

Например, вы можете проанализировать сотрудников какой-либо компании и попытаться установить зависимость от характеристик или переменных, таких как уровень образования, количество лет работы на текущей должности, возраст, зарплата, шансы на повышение и так далее. Набор данных, относящихся к одному сотруднику, представляет собой одно наблюдение. Признаки или переменные могут принимать одну из двух форм:

1. Независимые переменные, также называемые входными данными или предикторами, не зависят от других интересующих нас характеристик (или, по крайней мере, вы предполагаете это для целей анализа).
2. Зависимые переменные, также называемые выходными данными или откликами, зависят от независимых переменных.

В приведенном выше примере, когда вы анализируете сотрудников, вы можете предположить, что уровень образования, время работы на текущей должности и возраст не зависят друг от друга, и рассматривать их как исходные данные. Заработная плата и шансы на продвижение по службе могут быть результатами, которые зависят от затрат.

Примечание: Контролируемые алгоритмы машинного обучения анализируют ряд наблюдений и пытаются математически выразить зависимость между входными данными и выходными данными. Эти математические представления зависимостей являются моделями .

Характер зависимых переменных различает задачи регрессии и задачи классификации. Задачи регрессии имеют непрерывные и, как правило, неограниченные результаты. Примером может служить ситуация, когда вы оцениваете заработную плату в зависимости от опыта и уровня образования. С другой стороны, задачи классификации имеют дискретные и конечные результаты, называемые классами или категориями. Например, прогнозирование того, будет ли сотрудник повышен в должности или нет (правда это или ложь), является проблемой классификации.

Существует два основных типа проблем классификации:

1. Бинарная или биномиальная классификация: всего два класса на выбор (обычно 0 и 1, истина и ложь или положительное и отрицательное значения)
2. Многоклассовая или мультиномиальная классификация: три или более класса выходных данных на выбор

Если имеется только одна входная переменная, то она обычно обозначается через 𝑥. Для более чем одного входного сигнала вы обычно будете видеть векторную запись 𝐱 = (𝑥₁, ..., 𝑥ᵣ), где 𝑟 - это количество предикторов (или независимых признаков). Выходная переменная часто обозначается через 𝑦 и принимает значения 0 или 1.

Когда Вам Нужна Классификация?

Классификацию можно применять во многих областях науки и техники. Например, алгоритмы классификации текстов используются для разделения законных сообщений электронной почты на спам, а также положительных и отрицательных комментариев. Вы можете ознакомиться с Практической классификацией текстов с помощью Python и Keras, чтобы получить некоторое представление об этой теме. Другие примеры включают медицинские приложения, биологическую классификацию, кредитный рейтинг и многое другое.

Задачи распознавания изображений часто представляют как задачи классификации. Например, вы можете спросить, изображает ли изображение человеческое лицо или нет, мышь это или слон, или какую цифру от нуля до девяти оно обозначает, и так далее. Чтобы узнать больше об этом, ознакомьтесь с Традиционное распознавание лиц с помощью Python и Распознавание лиц с помощью Python, менее чем за 25 строк кода.

Обзор логистической регрессии

Логистическая регрессия - это фундаментальный метод классификации. Он относится к группе линейных классификаторов и в чем-то похож на полиномиальную и линейную регрессию. Логистическая регрессия выполняется быстро и относительно просто, и вам удобно интерпретировать результаты. Хотя по сути это метод бинарной классификации, он также может быть применен к задачам с несколькими классами.

Предварительные требования к математике

Вам потребуется понимание сигмовидной функции и функции натурального логарифма, чтобы понять, что такое логистическая регрессия и как она работает.

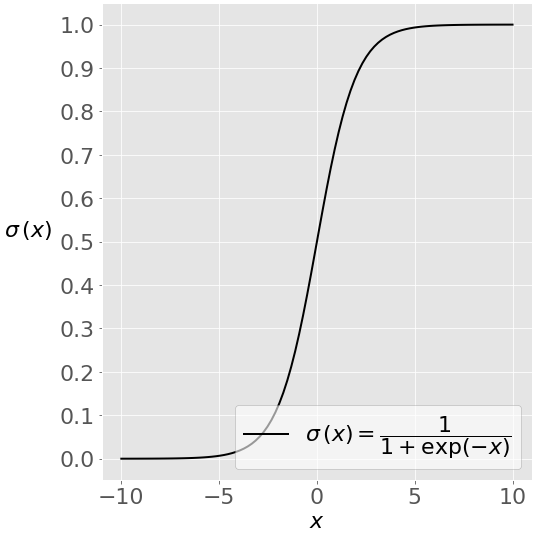
На этом рисунке показана сигмовидная функция (или S-образная кривая) некоторой переменной θ:

Сигмовидная функция имеет значения, очень близкие к 0 или 1, на большей части своей области. Этот факт делает ее пригодной для применения в методах классификации.

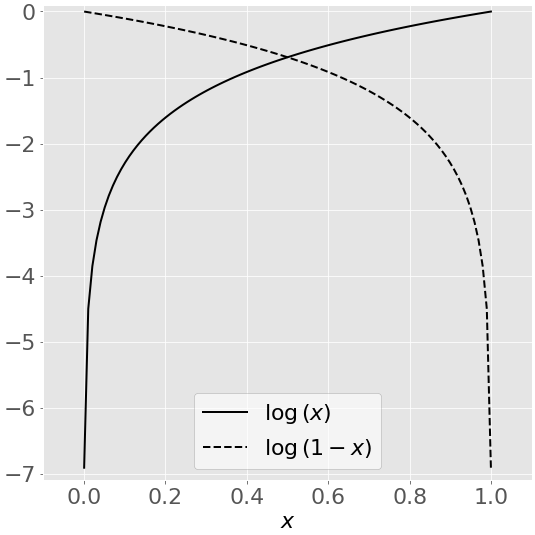
На этом рисунке показан натуральный логарифм(𝑥) некоторой переменной 𝑥 для значений 𝑥 от 0 до 1:

Когда θ приближается к нулю, натуральный логарифм θ стремится к отрицательной бесконечности. Когда θ = 1, log(θ) равен 0. Для log верно обратное(1 − 𝑥).

Обратите внимание, что часто натуральный логарифм обозначается как ln вместо log. В Python math.log(x) и numpy.log(x) представляют собой натуральный логарифм числа x, поэтому в этом руководстве вы будете следовать этим обозначениям.

Постановка задачи

В этом руководстве вы увидите объяснение распространенного случая логистической регрессии, применяемой к бинарной классификации. При реализации логистической регрессии ряда зависимой переменной 𝑦 на набор независимых переменных 𝐱 = (𝑥₁, ..., 𝑥ᵣ), где 𝑟 - количество предикторов ( или входов), вы начинаете с известными значениями предикторов 𝐱ᵢ и соответствующий фактический ответ (или выход) 𝑦ᵢ для каждого наблюдения 𝑖 = 1, ..., 𝑛.

Ваша цель - найти функцию логистической регрессии 𝑝(𝐱) такую, чтобы прогнозируемых отклика 𝑝(𝐱ᵢ) были такими максимально приближенный к фактическому ответу 𝑦ᵢ для каждого наблюдения 𝑖 = 1, ..., 𝑛. Помните, что в задачах бинарной классификации фактический ответ может быть только 0 или 1! Это означает, что каждое 𝑝(𝐱ᵢ) должно быть близко либо к 0, либо к 1. Вот почему удобно использовать сигмовидную функцию.

Если у вас есть функция логистической регрессии θ(θ), вы можете использовать ее для прогнозирования выходных данных для новых и невидимых входных данных, предполагая, что лежащая в основе математическая зависимость не меняется.

Методология

логистической регрессии является линейным классификатором, поэтому вы будете использовать линейную функцию 𝑓 ( 𝐱 ) = ₀ 𝑏 + 𝑏𝑥 ₁ ₁ + ⋯ + 𝑏𝑥ᵣ ᵣ, также называют логит. Переменные 𝑏₀, 𝑏₁, ..., 𝑏ᵣ являются оценочными коэффициентами регрессии, которые также называются прогнозируемыми весами или просто коэффициенты.

Функция логистической регрессии θ(θ) является сигмовидной функцией от 𝑓(𝐱): 𝑝(𝐱) = 1 / (1 + exp(−θ(θ)). Как таковая, она часто близка либо к 0, либо к 1. Функция θ(θ) часто интерпретируется как прогнозируемая вероятность того, что результат для данного θ равен 1. Следовательно, 1 − θ(θ) - это вероятность того, что результат равен 0.

логистическая регрессия определяет лучшие предсказал Весов 𝑏₀,₁𝑏, ..., 𝑏ᵣ такие, что функция 𝑝(𝐱) как можно ближе, чтобы все реальные ответы ᵢ𝑦, 𝑖 = 1, ..., 𝑛, где 𝑛 - число наблюдений. Процесс вычисления наилучших весовых коэффициентов с использованием доступных наблюдений называется обучением модели или подгонкой.

Чтобы получить наилучшие значения, вы обычно максимизируете логарифмическую функцию правдоподобия (LLF) для всех наблюдений θ = 1, ..., θ. Этот метод называется максимального правдоподобия оценки и представлена уравнением ЛЛФ = Σᵢ (ᵢ журнала𝑦(𝑝(𝐱ᵢ)) + (1 − 𝑦ᵢ) войти(1 − 𝑝(𝐱ᵢ))).

Когда θ = 0, значение LLF для соответствующего наблюдения равно log(1 - θ(θ)). Если значение θ(θ) близко к θ = 0, то значение log(1 − θ(θ)) близко к 0. Это желаемый результат. Если значение θ(θ) далеко от 0, то значение log(1 − θ(θ)) значительно уменьшается. Вам не нужен такой результат, потому что ваша цель - получить максимальное значение LLF. Аналогичным образом, когда ᵢ 𝑦 = 1, то ЛЛФ для наблюдения ᵢ журнала 𝑦(𝑝(𝐱ᵢ)). Если 𝑝(𝐱ᵢ) близка к ᵢ 𝑦 = 1, то log(𝑝(𝐱ᵢ)) близко к 0. Если 𝑝(𝐱ᵢ) далеко от 1, то log(𝑝(𝐱ᵢ)) - большое отрицательное число.

Существует несколько математических подходов, которые позволят рассчитать оптимальные веса, соответствующие максимальному LLF, но это выходит за рамки данного руководства. На данный момент вы можете доверить эти детали библиотекам Python для логистической регрессии, которые вы научитесь использовать здесь!

Как только вы определите наилучшие веса, определяющие функцию θ(θ), вы сможете получить прогнозируемые выходные значения θ(θ) для любого заданного входного сигнала θ. Для каждого наблюдения θ = 1, ..., θ прогнозируемый результат равен 1, если θ(θ) > 0,5, и 0 в противном случае. Пороговое значение не обязательно должно быть 0,5, но обычно оно равно этому. Вы можете задать меньшее или большее значение, если это более удобно для вашей ситуации.

Есть еще одна важная взаимосвязь между 𝑝(𝐱) и 𝑓(𝐱), которая заключается в том, что журнал(𝑝(𝐱) / (1 − 𝑝(𝐱))) = 𝑓(𝐱). Это равенство объясняет, почему 𝑓(𝐱) является логитом. Это означает, что 𝑝(𝐱) = 0,5 при 𝑓(𝐱) = 0 и что предсказал выход равен 1, если 𝑓 ( 𝐱 ) и gt; 0, и 0 в противном случае.

Эффективность классификации

Бинарная классификация имеет четыре возможных типа результатов:

1. Истинные отрицательные значения: правильно предсказанные отрицательные значения (нули)
2. Истинные положительные результаты: правильно предсказанные положительные результаты (единицы)
3. Ложноотрицательные результаты: неверно предсказанные отрицательные результаты (нули)
4. Ложные срабатывания: неверно предсказанные положительные срабатывания (единицы)

Обычно вы оцениваете производительность своего классификатора, сравнивая фактические и прогнозируемые выходные данные и подсчитывая правильные и неправильные прогнозы.

Наиболее простым показателем точности классификации является отношение числа правильных прогнозов к общему числу прогнозов (или наблюдений). К другим показателям бинарных классификаторов относятся следующие:

• положительное прогностическое значение - это отношение числа истинных срабатываний к сумме чисел истинных и ложных срабатываний.
• Отрицательное прогностическое значение представляет собой отношение числа истинно отрицательных результатов к сумме чисел истинно отрицательных и ложноотрицательных результатов.
• Чувствительность ( также известная как коэффициент запоминания или истинно положительный результат) - это отношение числа истинных положительных результатов к числу фактических положительных результатов.
• Специфичность ( или истинно отрицательный показатель) - это отношение числа истинно отрицательных результатов к числу фактических отрицательных результатов.

Наиболее подходящий показатель зависит от интересующей вас проблемы. В этом руководстве вы будете использовать наиболее простой способ определения точности классификации.

Логистическая регрессия с одной переменной

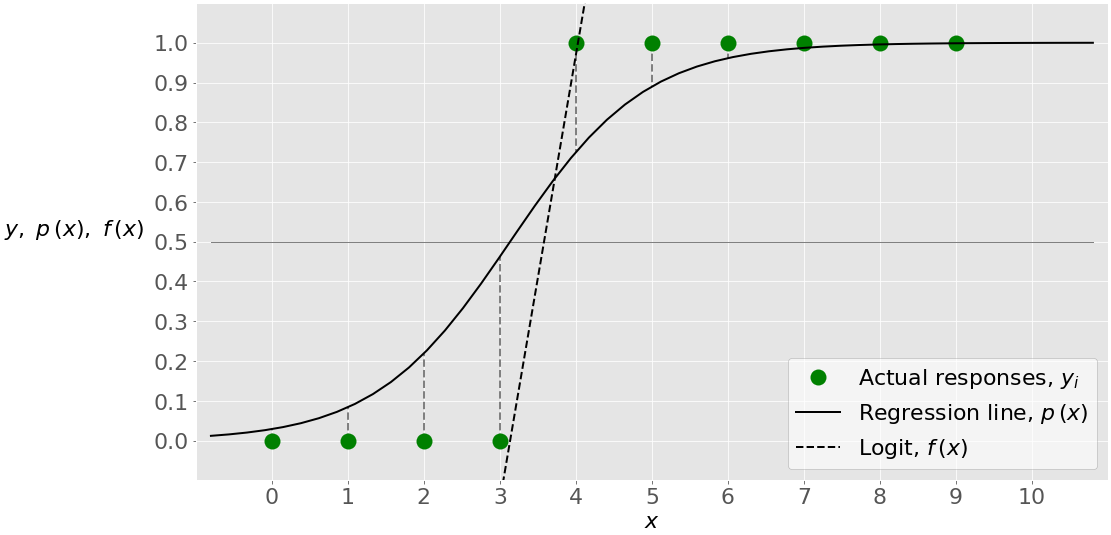
Логистическая регрессия с одной переменной является наиболее простым случаем логистической регрессии. Существует только одна независимая переменная (или признак), которая равна 𝐱 = 𝑥. Этот рисунок иллюстрирует логистическую регрессию с одной переменной:

Здесь у вас есть заданный набор пар ввода-вывода (или 𝑥-𝑦), обозначенных зелеными кружками. Это ваши наблюдения. Помните, что 𝑦 может быть только 0 или 1. Например, крайний левый зеленый кружок имеет входное значение θ = 0 и фактический выходной сигнал θ = 0. Крайнее правое наблюдение имеет θ = 9 и 𝑦 = 1.

логистическая регрессия находит Весов 𝑏и 𝑏 ₀ ₁ которые соответствуют максимальным ЛЛФ. Эти коэффициенты определяют логит 𝑓 ( 𝑥 ) = 𝑏₀+ 𝑏𝑥₁, которая является прерывистой черной линией. Они также определяют прогнозируемую вероятность 𝑝(𝑥) = 1 / (1 + exp(−𝑓(𝑥))), показанную здесь сплошной черной линией. В этом случае пороговое значение 𝑝(𝑥) = 0,5 и 𝑓(𝑥) = 0 соответствует значению 𝑥, немного превышающему 3. Это значение является пределом между входами с прогнозируемыми выходными значениями 0 и 1.

Многовариантная логистическая регрессия

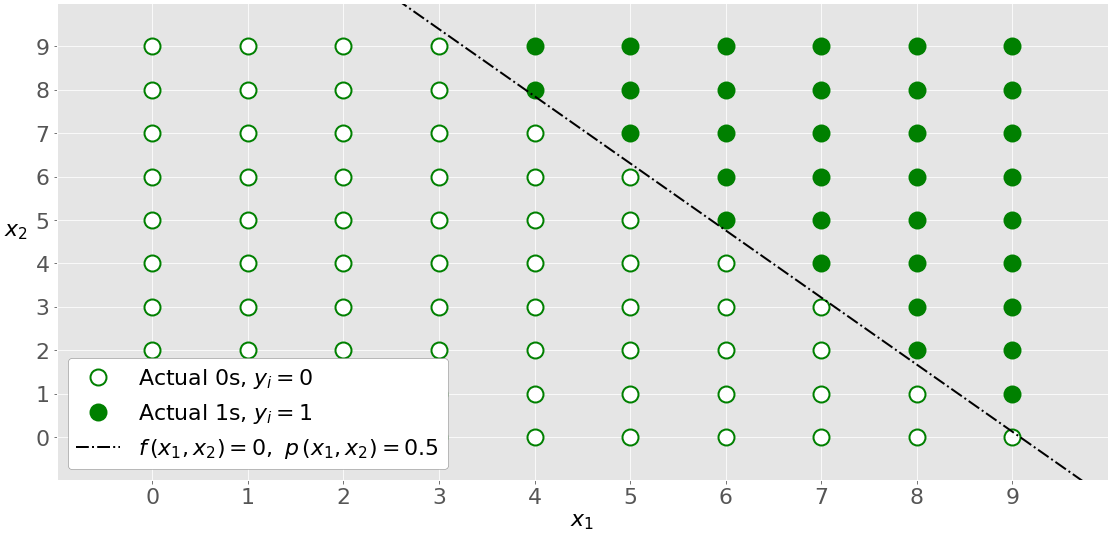
Многовариантная логистическая регрессия содержит более одной входной переменной. На этом рисунке показана классификация с двумя независимыми переменными 𝑥₁ и 𝑥₂:

График отличается от графика с одной переменной, поскольку обе оси представляют входные данные. Выходные данные также отличаются по цвету. Белыми кружками показаны наблюдения, классифицированные как нули, а зелеными - как единицы.

логистическая регрессия определяет 𝑏Весов₀, ₁ 𝑏и 𝑏₂ которые максимизируют ЛЛФ. После того, как вы 𝑏₀, ₁ 𝑏и 𝑏₂, вы можете сделать:

• Логит 𝑓(𝑥₁, 𝑥₂) = 𝑏₀ + 𝑏₁𝑥₁ + 𝑏₂𝑥₂
• Вероятности 𝑝(𝑥₁, 𝑥₂) = 1 / (1 + exp(-−(𝑥₁, 𝑥₂)))

штрихпунктирная линия черного цвета линейно разделяет на два класса. Эта линия соответствует 𝑝(𝑥₁, 𝑥₂) = 0,5 и 𝑓(𝑥 ₁ , ₂ 𝑥) = 0.

Регуляризация

Переобучение - это одна из самых серьезных проблем, связанных с машинным обучением. Это происходит, когда модель слишком хорошо усваивает обучающие данные. Затем модель изучает не только взаимосвязи между данными, но и шум в наборе данных. Переоборудованные модели, как правило, имеют хорошую производительность с данными, используемыми для их подгонки (обучающие данные), но они плохо работают с невидимыми данными (или тестовыми данными, которые не используются для подгонки модели).

Переобучение обычно происходит при работе со сложными моделями. Регуляризация обычно направлена на уменьшение сложности модели. Методы регуляризации, применяемые с логистической регрессией, в основном приводят к снижению больших коэффициентов 𝑏₀, 𝑏₁, ..., 𝑏ᵣ:

• Регуляризация L1 наказывает
• LLF масштабированной суммой абсолютных значений весов: |𝑏₀/|/|/+|+/𝑏ᵣ|.<|<4>>>
• Регуляризация L2 наказывает LLF масштабированной суммой квадратов весов: 𝑏₀2+𝑏₁2+⋯+𝑏ᵣ2.
• Регуляризация упругой сети представляет собой линейную комбинацию регуляризации L1 и L2.

Регуляризация может значительно повысить производительность модели на основе невидимых данных.

Логистическая регрессия в Python

Теперь, когда вы понимаете основы, вы готовы применить соответствующие пакеты, а также их функции и классы для выполнения логистической регрессии в Python. В этом разделе вы увидите следующее:

• Краткое описание пакетов Python для логистической регрессии (NumPy, scikit-learn, StatsModels и Matplotlib)
• Два наглядных примера логистической регрессии, решенной с помощью scikit-learn
• Один концептуальный пример, решенный с помощью StatsModels
• Один из реальных примеров классификации рукописных цифр

Давайте начнем внедрять логистическую регрессию на Python!

Пакеты Python для логистической регрессии

Есть несколько пакетов, которые вам понадобятся для логистической регрессии в Python. Все они бесплатны и с открытым исходным кодом, с большим количеством доступных ресурсов. Во-первых, вам понадобится NumPy, который является фундаментальным пакетом для научных и численных вычислений на Python. NumPy полезен и популярен, поскольку позволяет выполнять высокопроизводительные операции с одномерными и многомерными массивами.

В NumPy есть много полезных процедур работы с массивами. Он позволяет писать элегантный и компактный код и хорошо работает со многими пакетами Python. Если вы хотите изучить NumPy, то можете начать с официального руководства пользователя . Справочник по NumPy также содержит исчерпывающую документацию по его функциям, классам и методам.

Примечание: Чтобы узнать больше о производительности NumPy и других преимуществах, которые она может предложить, ознакомьтесь с Сравнением производительности Pure Python, NumPy и TensorFlow и Смотри, Мама, никаких for циклов: Программирование массивов с помощью NumPy.

Еще один пакет Python, который вы будете использовать, - это scikit-learn. Это одна из самых популярных библиотек для науки о данных и для машинного обучения. Вы можете использовать scikit-learn для выполнения различных функций:

• Предварительная обработка данных
• Уменьшить масштабность задач
• Проверка правильности моделей
• Выберите наиболее подходящую модель
• Решать задачи регрессии и классификации
• Внедрить кластерный анализ

Вы найдете полезную информацию на официальном веб-сайте scikit-learn , где вы, возможно, захотите прочитать о обобщенных линейных моделях и реализация логистической регрессии. Если вам нужна функциональность, которую не может предложить scikit-learn, то вам могут пригодиться StatsModels. Это мощная библиотека Python для статистического анализа. Вы можете найти более подробную информацию на официальном сайте .

Наконец, вы будете использовать Matplotlib для визуализации результатов вашей классификации. Это всеобъемлющая библиотека Python, которая широко используется для высококачественного построения графиков. Дополнительную информацию вы можете найти на официальном веб-сайте и в руководстве пользователя . Существует несколько ресурсов для изучения Matplotlib, которые могут оказаться полезными, например, официальные учебники , Анатомия Matplotlib и Построение графиков на Python С помощью Matplotlib (руководство).

Логистическая регрессия в Python с помощью scikit-learn: Пример 1

Первый пример относится к задаче бинарной классификации с одной переменной. Это наиболее простая задача классификации. При подготовке моделей классификации необходимо выполнить несколько общих шагов:

1. Импорт пакетов, функций и классов
2. Получите данные для работы и, при необходимости, преобразуйте их
3. Создайте классификационную модель и обработайте (или подогните) ее к имеющимся у вас данным
4. Оцените свою модель, чтобы убедиться в ее удовлетворительной производительности

Выбранная вами достаточно хорошая модель может быть использована для дальнейших прогнозов, связанных с новыми, невидимыми данными. Описанная выше процедура одинакова для классификации и регрессии.

Шаг 1: Импорт пакетов, функций и классов

Сначала вам нужно импортировать Matplotlib для визуализации и NumPy для операций с массивами. Вам также понадобятся LogisticRegression, classification_report(), и confusion_matrix() из scikit-learn:

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix

Теперь вы импортировали все необходимое для логистической регрессии в Python с помощью scikit-learn!

Шаг 2: Получение данных

На практике у вас обычно есть какие-то данные для работы. Для целей этого примера давайте просто создадим массивы для входных (𝑥) и выходных (𝑦) значений:

x = np.arange(10).reshape(-1, 1)
y = np.array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1])

Входными и выходными данными должны быть массивы NumPy (экземпляры класса numpy.ndarray) или аналогичные объекты. numpy.arange() создает массив последовательных значений с равными интервалами в заданном диапазоне. Для получения дополнительной информации об этой функции ознакомьтесь с официальной документацией или NumPy arange(): Как использовать np.arange().

Массив x должен быть двумерным. В нем должен быть один столбец для каждого входного сигнала, а количество строк должно быть равно количеству наблюдений. Чтобы сделать x двумерным, вы применяете .reshape() с аргументами -1, чтобы получить столько строк, сколько необходимо, и 1, чтобы получить один столбец. Для получения дополнительной информации о .reshape() вы можете ознакомиться с официальной документацией . Вот как теперь выглядят x и y:

>>> x
array([[0],
       [1],
       [2],
       [3],
       [4],
       [5],
       [6],
       [7],
       [8],
       [9]])
>>> y
array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1])

x имеет два измерения:

1. Один столбец для одного входного сигнала
2. Десять строк, каждая из которых соответствует одному наблюдению

y является одномерным и содержит десять элементов. Опять же, каждый элемент соответствует одному наблюдению. Он содержит только нули и единицы, поскольку это задача бинарной классификации.

Шаг 3: Создайте модель и обучите ее

Подготовив входные и выходные данные, вы можете создать и определить свою классификационную модель. Вы собираетесь представить ее с помощью экземпляра класса LogisticRegression:

model = LogisticRegression(solver='liblinear', random_state=0)

Приведенный выше оператор создает экземпляр LogisticRegression и привязывает ссылки на него к переменной model. LogisticRegression имеет несколько необязательных параметров, которые определяют поведение модели и подхода:

• penalty представляет собой строку ('l2' по умолчанию), который определяет, есть ли является ли регуляризация и какой подход использовать. Другими вариантами являются 'l1', 'elasticnet', и 'none'.

• dual является логическим значением (False по умолчанию), которое определяет, следует ли использовать простую (когда False) или двойственную формулировку (когда True).

• tol это число с плавающей запятой (0.0001 по умолчанию), которое определяет допустимое значение для остановки процедуры.

• C это положительное число с плавающей запятой (1.0 по умолчанию), которое определяет относительную силу регуляризации. Меньшие значения указывают на более сильную регуляризацию.

• fit_intercept является логическим значением (True по умолчанию), которое определяет, следует ли вычислять перехват 𝑏₀ (когда True) или считать его равным нулю (когда False).

• intercept_scaling это число с плавающей запятой (1.0 по умолчанию), которое определяет масштаб пересечения 𝑏₀.

• class_weight это словарь 'balanced' или None (по умолчанию), который определяет веса, относящиеся к каждому классу. Когда None, все классы имеют одинаковый вес.

• random_state представляет собой целое число, экземпляр numpy.RandomState, или None (по умолчанию), который определяет, что псевдо-генератор случайных чисел для использования.

• solver это строка ('liblinear' по умолчанию), которая определяет, какой решатель использовать для подгонки модели. Другими вариантами являются 'newton-cg', 'lbfgs', 'sag', и 'saga'.

• max_iter это целое число (100 по умолчанию), которое определяет максимальное количество итераций, выполняемых решателем во время подгонки модели.

• multi_class это строка ('ovr' по умолчанию), которая определяет подход, используемый для обработки нескольких классов. Другими вариантами являются 'multinomial' и 'auto'.

• verbose является неотрицательным целым числом (0 по умолчанию), которое определяет детализацию для решателей 'liblinear' и 'lbfgs'.

• warm_start является логическим значением (False по умолчанию), которое определяет, следует ли повторно использовать ранее полученное решение.

• n_jobs это целое число или None (по умолчанию), которое определяет количество используемых параллельных процессов. None обычно означает использование одного ядра, в то время как -1 означает использование всех доступных ядер.

• l1_ratio это либо число с плавающей запятой от нуля до единицы, либо None (по умолчанию). Это определяет относительную важность части L1 в регуляризации упругой сети.

Вам следует тщательно подбирать решатель и метод регуляризации по нескольким причинам:

• 'liblinear' решатель не работает без регуляризации.
• 'newton-cg', 'sag', 'saga', и 'lbfgs' не поддерживают регуляризацию L1.
• 'saga' это единственный решатель, поддерживающий регуляризацию эластичной сети.

Как только модель создана, ее необходимо подогнать (или обучить). Подгонка модели - это процесс определения коэффициентов 𝑏₀, 𝑏₁, ..., 𝑏ᵣ, которые соответствуют наилучшему значению функции затрат. Вы соответствуете модели с .fit():

model.fit(x, y)

.fit() принимает значения x, y, и, возможно, веса, связанные с наблюдениями. Затем он соответствует модели и возвращает сам экземпляр модели:

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='warn', n_jobs=None, penalty='l2',
                   random_state=0, solver='liblinear', tol=0.0001, verbose=0,
                   warm_start=False)

Это полученное строковое представление установленной модели.

Вы можете использовать тот факт, что .fit() возвращает экземпляр модели, и связать последние два оператора в цепочку. Они эквивалентны следующей строке кода:

model = LogisticRegression(solver='liblinear', random_state=0).fit(x, y)

На этом этапе у вас есть определенная модель классификации.

Вы можете быстро получить атрибуты вашей модели. Например, атрибут .classes_ представляет собой массив различных значений, которые принимает y:

>>> model.classes_
array([0, 1])

Это пример бинарной классификации, и y может быть 0 или 1, как указано выше.

Вы также можете получить значение наклона θ и пересечения θ линейной функции θ следующим образом:

>>> model.intercept_
array([-1.04608067])
>>> model.coef_
array([[0.51491375]])

Как вы можете видеть, 𝑏₀ задается внутри одномерного массива, в то время как 𝑏₁ находится внутри двумерного массива. Для получения этих результатов используются атрибуты .intercept_ и .coef_.

Шаг 4: Оцените модель

Как только модель определена, вы можете проверить ее работоспособность с помощью .predict_proba(), которая возвращает матрицу вероятностей того, что прогнозируемый результат равен нулю или единице:

>>> model.predict_proba(x)
array([[0.74002157, 0.25997843],
       [0.62975524, 0.37024476],
       [0.5040632 , 0.4959368 ],
       [0.37785549, 0.62214451],
       [0.26628093, 0.73371907],
       [0.17821501, 0.82178499],
       [0.11472079, 0.88527921],
       [0.07186982, 0.92813018],
       [0.04422513, 0.95577487],
       [0.02690569, 0.97309431]])

В приведенной выше матрице каждая строка соответствует отдельному наблюдению. В первом столбце указана вероятность того, что прогнозируемый результат будет равен нулю, то есть 1 - 𝑝(𝑥). Второй столбец - это вероятность того, что результат равен единице, или 𝑝(𝑥).

Вы можете получить фактические прогнозы, основанные на матрице вероятностей и значениях 𝑝(𝑥), с помощью .predict():

>>> model.predict(x)
array([0, 0, 0, 1, 1, 1, 1, 1, 1, 1])

Эта функция возвращает прогнозируемые выходные значения в виде одномерного массива.

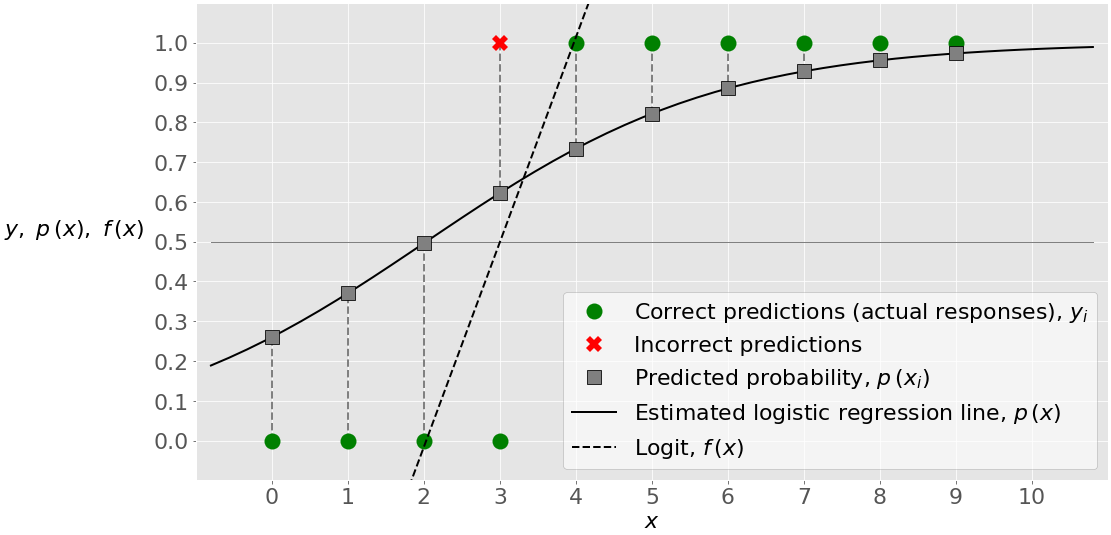
На рисунке ниже показаны входные данные, выходные данные и результаты классификации:

Зеленые кружки обозначают фактические ответы, а также правильные прогнозы. Красный символ × показывает неверный прогноз. Сплошная черная линия - это расчетная линия логистической регрессии 𝑝(𝑥). Серые квадраты - это точки на этой прямой, которые соответствуют 𝑥 и значениям во втором столбце матрицы вероятностей. Черная пунктирная линия - это логарифм 𝑓(𝑥).

значение 𝑥 чуть выше 2 соответствует порога 𝑝(𝑥)=0,5, что 𝑓(𝑥)=0. Эта величина 𝑥 является границей между точками, которые классифицируются как нули и те, которые были предсказаны как те.

Например, первая точка имеет входные данные θ=0, фактический выходной сигнал θ=0, вероятность θ=0,26 и прогнозируемое значение, равное 0. Вторая точка имеет значение 𝑥=1, 𝑦=0, 𝑝=0.37, и прогноз, равный 0. Только четвертая точка имеет фактический результат 𝑦=0 и вероятность выше 0,5 (при 𝑝=0,62), поэтому она ошибочно классифицируется как 1. Все остальные значения предсказаны правильно.

Если девять из десяти наблюдений классифицированы правильно, точность вашей модели равна 9/10=0,9, которую вы можете получить с помощью .score():

>>> model.score(x, y)
0.9

.score() принимает входные и выходные данные в качестве аргументов и возвращает отношение количества правильных прогнозов к количеству наблюдений.

Вы можете получить дополнительную информацию о точности модели с помощью матрицы путаницы. В случае бинарной классификации матрица путаницы содержит следующие числа:

• Истинные негативы в верхнем левом углу
• Ложноотрицательные результаты в левом нижнем углу
• Ложные срабатывания в правом верхнем углу
• Истинные срабатывания в правом нижнем углу

Чтобы создать матрицу путаницы, вы можете использовать confusion_matrix() и указать фактические и прогнозируемые выходные данные в качестве аргументов:

>>> confusion_matrix(y, model.predict(x))
array([[3, 1],
       [0, 6]])

Полученная матрица показывает следующее:

• Три истинных отрицательных прогноза: Первые три наблюдения - это правильно предсказанные нули.
• Никаких ложноотрицательных прогнозов: Это те, которые ошибочно были предсказаны как нули.
• Одно ложноположительное предсказание: Четвертое наблюдение - это ноль, который был ошибочно предсказан как единица.
• Шесть истинных положительных предсказаний: Последние шесть наблюдений были предсказаны правильно.

Часто бывает полезно визуализировать матрицу путаницы. Вы можете сделать это с помощью .imshow() из Matplotlib, который принимает матрицу путаницы в качестве аргумента:

cm = confusion_matrix(y, model.predict(x))

fig, ax = plt.subplots(figsize=(8, 8))
ax.imshow(cm)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1), ticklabels=('Predicted 0s', 'Predicted 1s'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('Actual 0s', 'Actual 1s'))
ax.set_ylim(1.5, -0.5)
for i in range(2):
    for j in range(2):
        ax.text(j, i, cm[i, j], ha='center', va='center', color='red')
plt.show()

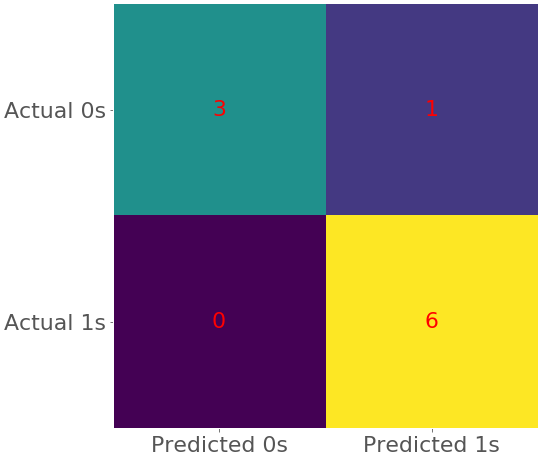
Приведенный выше код создает тепловую карту, которая представляет матрицу путаницы:

На этом рисунке разные цвета обозначают разные числа, а похожие цвета - похожие числа. Тепловые карты - это удобный способ представления матрицы. Чтобы узнать о них больше, ознакомьтесь с документацией Matplotlib по Созданию аннотированных тепловых карт и .imshow().

Вы можете получить более полный отчет о классификации с помощью classification_report():

>>> print(classification_report(y, model.predict(x)))
              precision    recall  f1-score   support

           0       1.00      0.75      0.86         4
           1       0.86      1.00      0.92         6

    accuracy                           0.90        10
   macro avg       0.93      0.88      0.89        10
weighted avg       0.91      0.90      0.90        10

Эта функция также принимает фактические и прогнозируемые выходные данные в качестве аргументов. Она возвращает отчет о классификации в виде словаря, если вы указали output_dict=True или строку в противном случае.

Примечание: Обычно лучше оценивать вашу модель с помощью данных, которые вы не использовали для обучения. Так вы избежите предвзятости и обнаружите переобучение. Далее в этом руководстве вы увидите пример.

Для получения дополнительной информации о LogisticRegression ознакомьтесь с официальной документацией . Кроме того, scikit-learn предлагает аналогичный класс LogisticRegressionCV, который больше подходит для перекрестной проверки. Вы также можете ознакомиться с официальной документацией, чтобы узнать больше о отчетах о классификации и матрицах путаницы.

Улучшите модель

Вы можете улучшить свою модель, установив различные параметры. Например, давайте будем работать с параметром регуляризации C, равным 10.0, вместо значения по умолчанию 1.0:

model = LogisticRegression(solver='liblinear', C=10.0, random_state=0)
model.fit(x, y)

Теперь у вас есть другая модель с другими параметрами. У нее также будет другая матрица вероятностей и другой набор коэффициентов и прогнозов:

>>> model.intercept_
array([-3.51335372])
>>> model.coef_
array([[1.12066084]])
>>> model.predict_proba(x)
array([[0.97106534, 0.02893466],
       [0.9162684 , 0.0837316 ],
       [0.7810904 , 0.2189096 ],
       [0.53777071, 0.46222929],
       [0.27502212, 0.72497788],
       [0.11007743, 0.88992257],
       [0.03876835, 0.96123165],
       [0.01298011, 0.98701989],
       [0.0042697 , 0.9957303 ],
       [0.00139621, 0.99860379]])
>>> model.predict(x)
array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1])

Как вы можете видеть, абсолютные значения пересечения θ и коэффициента θ больше. Это происходит потому, что большее значение C означает более слабую регуляризацию или более слабое наказание, связанное с высокими значениями 𝑏₀ и 𝑏₁.

разных значений 𝑏и 𝑏 ₀ ₁ предполагают изменение логит 𝑓(𝑥), для различных значений вероятностей 𝑝(𝑥), различные формы линии регрессии, и, возможно, изменения в других прогнозируемых результатов и классификации. Граничное значение θ, для которого θ(θ)=0,5 и θ(θ)=0, теперь выше. Оно выше 3. В этом случае вы получаете все достоверные прогнозы, как показано в отчете о точности, путанице и классификации:

>>> model.score(x, y)
1.0
>>> confusion_matrix(y, model.predict(x))
array([[4, 0],
       [0, 6]])
>>> print(classification_report(y, model.predict(x)))
              precision    recall  f1-score   support

           0       1.00      1.00      1.00         4
           1       1.00      1.00      1.00         6

    accuracy                           1.00        10
   macro avg       1.00      1.00      1.00        10
weighted avg       1.00      1.00      1.00        10

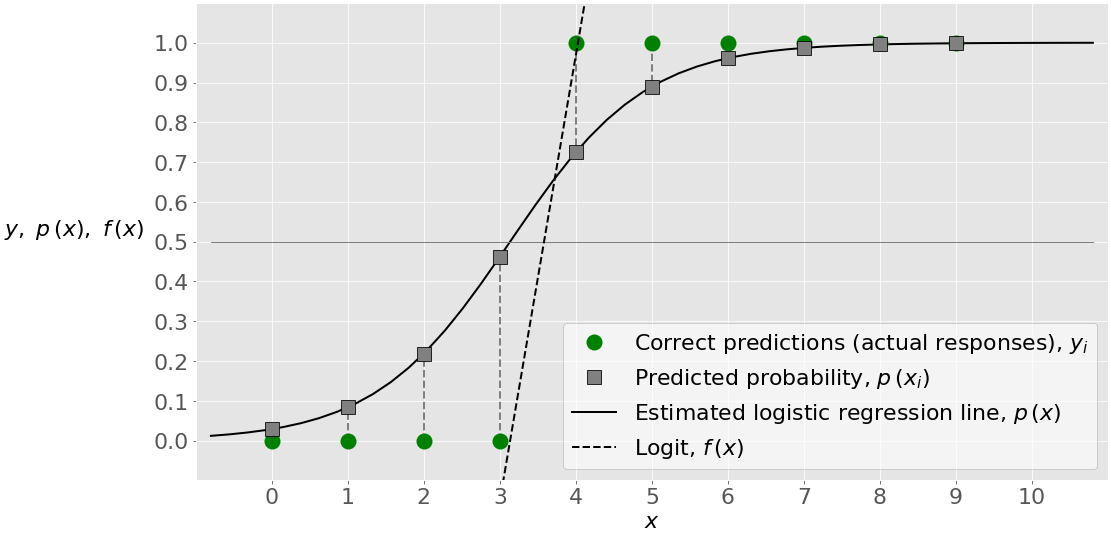
Оценка (или точность), равная 1, и нули в нижнем левом и верхнем правом полях матрицы путаницы указывают на то, что фактический и прогнозируемый результаты совпадают. Это также показано на рисунке ниже:

На этом рисунке показано, что расчетная линия регрессии теперь имеет другую форму и что четвертая точка правильно классифицируется как 0. Здесь нет красного символа ×, поэтому неверного прогноза нет.

Логистическая регрессия в Python с помощью scikit-learn: Пример 2

Давайте решим другую задачу классификации. Она аналогична предыдущей, за исключением того, что выходные данные отличаются по второму значению. Код аналогичен предыдущему случаю:

# Step 1: Import packages, functions, and classes
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix

# Step 2: Get data
x = np.arange(10).reshape(-1, 1)
y = np.array([0, 1, 0, 0, 1, 1, 1, 1, 1, 1])

# Step 3: Create a model and train it
model = LogisticRegression(solver='liblinear', C=10.0, random_state=0)
model.fit(x, y)

# Step 4: Evaluate the model
p_pred = model.predict_proba(x)
y_pred = model.predict(x)
score_ = model.score(x, y)
conf_m = confusion_matrix(y, y_pred)
report = classification_report(y, y_pred)

Этот пример классификационного кода выдает следующие результаты:

>>> print('x:', x, sep='\n')
x:
[[0]
 [1]
 [2]
 [3]
 [4]
 [5]
 [6]
 [7]
 [8]
 [9]]
>>> print('y:', y, sep='\n', end='\n\n')
y:
[0 1 0 0 1 1 1 1 1 1]

>>> print('intercept:', model.intercept_)
intercept: [-1.51632619]
>>> print('coef:', model.coef_, end='\n\n')
coef: [[0.703457]]

>>> print('p_pred:', p_pred, sep='\n', end='\n\n')
p_pred:
[[0.81999686 0.18000314]
 [0.69272057 0.30727943]
 [0.52732579 0.47267421]
 [0.35570732 0.64429268]
 [0.21458576 0.78541424]
 [0.11910229 0.88089771]
 [0.06271329 0.93728671]
 [0.03205032 0.96794968]
 [0.0161218  0.9838782 ]
 [0.00804372 0.99195628]]

>>> print('y_pred:', y_pred, end='\n\n')
y_pred: [0 0 0 1 1 1 1 1 1 1]

>>> print('score_:', score_, end='\n\n')
score_: 0.8

>>> print('conf_m:', conf_m, sep='\n', end='\n\n')
conf_m:
[[2 1]
 [1 6]]

>>> print('report:', report, sep='\n')
report:
              precision    recall  f1-score   support

           0       0.67      0.67      0.67         3
           1       0.86      0.86      0.86         7

    accuracy                           0.80        10
   macro avg       0.76      0.76      0.76        10
weighted avg       0.80      0.80      0.80        10

В данном случае оценка (или точность) равна 0,8. Два наблюдения классифицированы неверно. Одно из них является ложноотрицательным, а другое - ложноположительным.

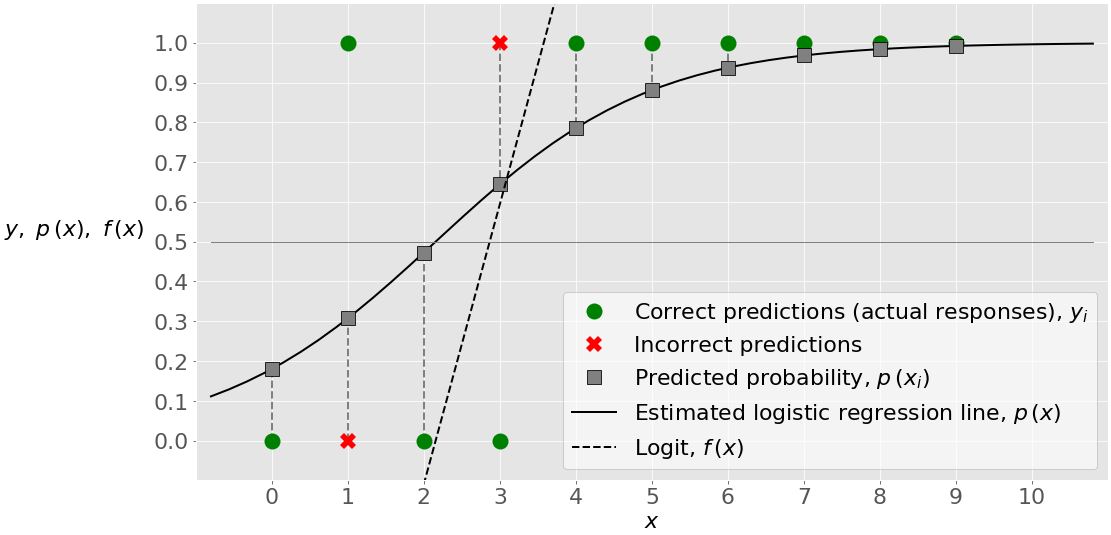
На рисунке ниже показан этот пример с восемью правильными и двумя неправильными предсказаниями:

Этот рисунок показывает одну важную характеристику этого примера. В отличие от предыдущего, эта задача не является линейно разделяемой. Это означает, что вы не можете найти значение θ и провести прямую линию, чтобы разделить наблюдения с θ=0 и с θ=1. Такой линии нет. Имейте в виду, что логистическая регрессия - это, по сути, линейный классификатор, поэтому теоретически вы не можете построить модель логистической регрессии с точностью до 1 в этом случае.

Логистическая регрессия в Python с использованием StatsModels: пример

Вы также можете реализовать логистическую регрессию на Python с помощью пакета StatsModels. Обычно это требуется, когда требуется больше статистических данных, связанных с моделями и результатами. Процедура аналогична процедуре scikit-learn.

Шаг 1: Импорт пакетов

Все, что вам нужно для импорта - это NumPy и statsmodels.api:

import numpy as np
import statsmodels.api as sm

Теперь у вас есть необходимые пакеты.

Шаг 2: Получение данных

Вы можете получать входные и выходные данные таким же образом, как и в scikit-learn. Однако StatsModels не учитывает перехват 𝑏₀, и вам нужно включить дополнительный столбец единиц в x. Вы делаете это с помощью add_constant():

x = np.arange(10).reshape(-1, 1)
y = np.array([0, 1, 0, 0, 1, 1, 1, 1, 1, 1])
x = sm.add_constant(x)

add_constant() принимает массив x в качестве аргумента и возвращает новый массив с дополнительным столбцом единиц. Вот как выглядят x и y:

>>> x
array([[1., 0.],
       [1., 1.],
       [1., 2.],
       [1., 3.],
       [1., 4.],
       [1., 5.],
       [1., 6.],
       [1., 7.],
       [1., 8.],
       [1., 9.]])
>>> y
array([0, 1, 0, 0, 1, 1, 1, 1, 1, 1])

Это ваши данные. Первый столбец x соответствует точке пересечения 𝑏₀. Второй столбец содержит исходные значения x.

Шаг 3: Создайте модель и обучите ее

Ваша модель логистической регрессии будет экземпляром класса statsmodels.discrete.discrete_model.Logit. Вот как вы можете создать такую модель:

>>> model = sm.Logit(y, x)

Обратите внимание, что первым аргументом здесь является y, за которым следует x.

Теперь вы создали свою модель и должны согласовать ее с существующими данными. Вы делаете это с помощью .fit() или, если вы хотите применить регуляризацию L1, с помощью .fit_regularized():

>>> result = model.fit(method='newton')
Optimization terminated successfully.
         Current function value: 0.350471
         Iterations 7

Теперь модель готова, а переменная result содержит полезные данные. Например, вы можете получить значения 𝑏₀ и 𝑏₁ с помощью .params:

>>> result.params
array([-1.972805  ,  0.82240094])

Первым элементом полученного массива является точка пересечения θ, а вторым - угол наклона θ. Для получения дополнительной информации вы можете ознакомиться с официальной документацией по Logit,, а также .fit() и .fit_regularized().

Шаг 4: Оцените модель

Вы можете использовать results для получения вероятности того, что прогнозируемые результаты будут равны единице:

>>> result.predict(x)
array([0.12208792, 0.24041529, 0.41872657, 0.62114189, 0.78864861,
       0.89465521, 0.95080891, 0.97777369, 0.99011108, 0.99563083])

Эти вероятности вычисляются с помощью .predict(). Вы можете использовать их значения для получения фактических прогнозируемых результатов:

>>> (result.predict(x) >= 0.5).astype(int)
array([0, 0, 0, 1, 1, 1, 1, 1, 1, 1])

Полученный массив содержит прогнозируемые выходные значения. Как вы можете видеть, 𝑏₀, 𝑏₁ и вероятности, полученные с помощью scikit-learn и StatsModels, различны. Это является следствием применения различных итеративных и приближенных процедур и параметров. Однако в этом случае вы получаете те же прогнозируемые результаты, что и при использовании scikit-learn.

Вы можете получить матрицу путаницы с помощью .pred_table():

>>> result.pred_table()
array([[2., 1.],
       [1., 6.]])

Этот пример такой же, как и при использовании scikit-learn, поскольку прогнозируемые результаты одинаковы. Матрицы путаницы, полученные с помощью StatsModels и scikit-learn, отличаются типами своих элементов (числа с плавающей запятой и целые числа).

.summary() и .summary2() получите выходные данные, которые могут оказаться полезными в некоторых обстоятельствах:

>>> result.summary()
<class 'statsmodels.iolib.summary.Summary'>
"""
                           Logit Regression Results                           
==============================================================================
Dep. Variable:                      y   No. Observations:                   10
Model:                          Logit   Df Residuals:                        8
Method:                           MLE   Df Model:                            1
Date:                Sun, 23 Jun 2019   Pseudo R-squ.:                  0.4263
Time:                        21:43:49   Log-Likelihood:                -3.5047
converged:                       True   LL-Null:                       -6.1086
                                        LLR p-value:                   0.02248
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const         -1.9728      1.737     -1.136      0.256      -5.377       1.431
x1             0.8224      0.528      1.557      0.119      -0.213       1.858
==============================================================================
"""
>>> result.summary2()
<class 'statsmodels.iolib.summary2.Summary'>
"""
                        Results: Logit
===============================================================
Model:              Logit            Pseudo R-squared: 0.426   
Dependent Variable: y                AIC:              11.0094
Date:               2019-06-23 21:43 BIC:              11.6146
No. Observations:   10               Log-Likelihood:   -3.5047
Df Model:           1                LL-Null:          -6.1086
Df Residuals:       8                LLR p-value:      0.022485
Converged:          1.0000           Scale:            1.0000  
No. Iterations:     7.0000                                     
-----------------------------------------------------------------
          Coef.    Std.Err.      z      P>|z|     [0.025   0.975]
-----------------------------------------------------------------
const    -1.9728     1.7366   -1.1360   0.2560   -5.3765   1.4309
x1        0.8224     0.5281    1.5572   0.1194   -0.2127   1.8575
===============================================================

"""

Это подробные отчеты со значениями, которые вы можете получить с помощью соответствующих методов и атрибутов. Для получения дополнительной информации ознакомьтесь с официальной документацией, относящейся к LogitResults.

Логистическая регрессия в Python: распознавание рукописного ввода

Предыдущие примеры иллюстрировали реализацию логистической регрессии в Python, а также некоторые детали, связанные с этим методом. Следующий пример покажет вам, как использовать логистическую регрессию для решения реальной задачи классификации. Этот подход очень похож на тот, что вы уже видели, но с большим набором данных и рядом дополнительных проблем.

В этом примере речь идет о распознавании изображений. Если быть более точным, вы будете работать над распознаванием рукописных цифр. Вы будете использовать набор данных из 1797 наблюдений, каждое из которых представляет собой изображение одной цифры, написанной от руки. Каждое изображение имеет размер 64 пикселя, ширину 8 пикселей и высоту 8 пикселей.

Примечание: Чтобы узнать больше об этом наборе данных, ознакомьтесь с официальной документацией .

Входные данные (𝐱) представляют собой векторы с 64 измерениями или значениями. Каждый входной вектор описывает одно изображение. Каждое из 64 значений представляет один пиксель изображения. Входными значениями являются целые числа от 0 до 16, в зависимости от оттенка серого для соответствующего пикселя. Результатом является (𝑦) для каждого наблюдения целое число от 0 до 9, соответствующее цифре на изображении. Всего существует десять классов, каждый из которых соответствует одному изображению.

Шаг 1: Импорт пакетов

Вам нужно будет импортировать Matplotlib, NumPy и несколько функций и классов из scikit-learn:

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

Вот и все! У вас есть все функциональные возможности, необходимые для выполнения классификации.

Шаг 2а: Получение данных

Вы можете получить набор данных непосредственно из scikit-learn с помощью load_digits(). Он возвращает набор входных и выходных данных:

x, y = load_digits(return_X_y=True)

Теперь у вас есть данные. Вот как выглядят x и y:

>>> x
array([[ 0.,  0.,  5., ...,  0.,  0.,  0.],
       [ 0.,  0.,  0., ..., 10.,  0.,  0.],
       [ 0.,  0.,  0., ..., 16.,  9.,  0.],
       ...,
       [ 0.,  0.,  1., ...,  6.,  0.,  0.],
       [ 0.,  0.,  2., ..., 12.,  0.,  0.],
       [ 0.,  0., 10., ..., 12.,  1.,  0.]])
>>> y
array([0, 1, 2, ..., 8, 9, 8])

Это ваши данные для работы. x представляет собой многомерный массив из 1797 строк и 64 столбцов. Он содержит целые числа от 0 до 16. y представляет собой одномерный массив, содержащий 1797 целых чисел от 0 до 9.

Шаг 2b: Разделение данных

Хорошей и широко распространенной практикой является разделение набора данных, с которым вы работаете, на два подмножества. Это обучающий набор и тестовый набор. Это разделение обычно выполняется случайным образом. Вы должны использовать обучающий набор в соответствии с вашей моделью. После того, как модель настроена, вы оцениваете ее производительность с помощью тестового набора. Важно не использовать тестовый набор в процессе настройки модели. Такой подход позволяет объективно оценить модель.

Один из способов разделить набор данных на обучающий и тестовый наборы - это применить train_test_split():

x_train, x_test, y_train, y_test =\
    train_test_split(x, y, test_size=0.2, random_state=0)

train_test_split() принимает x и y. Он также принимает test_size, который определяет размер тестового набора, и random_state для определения состояния генератора псевдослучайных чисел, а также другие необязательные аргументы. Эта функция возвращает список с четырьмя массивами:

1. x_train: часть x, используемая для подгонки модели
2. x_test: часть x, используемая для оценки модели
3. y_train: часть y, соответствующая x_train
4. y_test: часть y, которая соответствует x_test

Как только ваши данные будут разделены, вы можете забыть о x_test и y_test до тех пор, пока не определите свою модель.

Шаг 2c: Масштабирование данных

Стандартизация - это процесс преобразования данных таким образом, что среднее значение каждого столбца становится равным нулю, а стандартное отклонение каждого столбца равно единице. Таким образом, вы получите одинаковый масштаб для всех столбцов. Выполните следующие действия для стандартизации ваших данных:

1. Вычислите среднее значение и стандартное отклонение для каждого столбца.
2. Вычтите соответствующее среднее значение из каждого элемента.
3. Разделите полученную разницу на соответствующее стандартное отклонение.

Рекомендуется стандартизировать входные данные, которые вы используете для логистической регрессии, хотя во многих случаях в этом нет необходимости. Стандартизация может повысить производительность вашего алгоритма. Это помогает, если вам нужно сравнить и интерпретировать веса. Это важно, когда вы применяете штрафные санкции, потому что алгоритм фактически применяет штрафные санкции при больших значениях весов.

Вы можете стандартизировать свои входные данные, создав экземпляр StandardScaler и вызвав для него .fit_transform():

scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)

.fit_transform() помещает экземпляр StandardScaler в массив, переданный в качестве аргумента, преобразует этот массив и возвращает новый, стандартизированный массив. Итак, x_train - это стандартизированный входной массив.

Шаг 3: Создайте модель и обучите ее

Этот шаг очень похож на предыдущие примеры. Единственное отличие заключается в том, что вы используете подмножества x_train и y_train для соответствия модели. Опять же, вы должны создать экземпляр LogisticRegression и вызвать для него .fit():

model = LogisticRegression(solver='liblinear', C=0.05, multi_class='ovr',
                           random_state=0)
model.fit(x_train, y_train)

Когда вы работаете с задачами, содержащими более двух классов, вам следует указать параметр multi_class из LogisticRegression. Он определяет, как решить проблему:

• 'ovr' сказано, чтобы двоичный файл соответствовал каждому классу.
• 'multinomial' говорит о необходимости применения полиномиальной подгонки потерь.

Последний оператор выдает следующий результат, поскольку .fit() возвращает саму модель:

LogisticRegression(C=0.05, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='ovr', n_jobs=None, penalty='l2', random_state=0,
                   solver='liblinear', tol=0.0001, verbose=0, warm_start=False)

Это параметры вашей модели. Теперь она определена и готова к следующему шагу.

Шаг 4: Оцените модель

Вы должны оценить свою модель аналогично тому, что вы делали в предыдущих примерах, с той разницей, что в основном вы будете использовать x_test и y_test, которые являются подмножествами, не применяемыми для обучения. Если вы решили стандартизировать x_train, то полученная модель основана на масштабированных данных, поэтому x_test также следует масштабировать с помощью того же экземпляра StandardScaler:

x_test = scaler.transform(x_test)

Вот как вы получаете новый, правильно масштабированный x_test. В этом случае вы используете .transform(), который только преобразует аргумент, не устанавливая масштабатор.

Вы можете получить прогнозируемые выходные данные с помощью .predict():

y_pred = model.predict(x_test)

Переменная y_pred теперь привязана к массиву прогнозируемых выходных данных. Обратите внимание, что в качестве аргумента здесь используется x_test.

Вы можете получить точность с помощью .score():

>>> model.score(x_train, y_train)
0.964509394572025
>>> model.score(x_test, y_test)
0.9416666666666667

На самом деле, вы можете получить два значения точности, одно из которых получено с помощью обучающего набора, а другое - с помощью тестового набора. Возможно, было бы неплохо сравнить их, поскольку ситуация, когда точность обучающего набора намного выше, может указывать на переобучение. Точность тестового набора более важна для оценки производительности на невидимых данных, поскольку она не является предвзятой.

Вы можете получить матрицу путаницы с помощью confusion_matrix():

>>> confusion_matrix(y_test, y_pred)
array([[27,  0,  0,  0,  0,  0,  0,  0,  0,  0],
       [ 0, 32,  0,  0,  0,  0,  1,  0,  1,  1],
       [ 1,  1, 33,  1,  0,  0,  0,  0,  0,  0],
       [ 0,  0,  1, 28,  0,  0,  0,  0,  0,  0],
       [ 0,  0,  0,  0, 29,  0,  0,  1,  0,  0],
       [ 0,  0,  0,  0,  0, 39,  0,  0,  0,  1],
       [ 0,  1,  0,  0,  0,  0, 43,  0,  0,  0],
       [ 0,  0,  0,  0,  0,  0,  0, 39,  0,  0],
       [ 0,  2,  1,  2,  0,  0,  0,  1, 33,  0],
       [ 0,  0,  0,  1,  0,  1,  0,  2,  1, 36]])

Полученная матрица путаницы велика. В данном случае она содержит 100 чисел. Это ситуация, когда было бы действительно полезно визуализировать ее:

cm = confusion_matrix(y_test, y_pred)

fig, ax = plt.subplots(figsize=(8, 8))
ax.imshow(cm)
ax.grid(False)
ax.set_xlabel('Predicted outputs', fontsize=font_size, color='black')
ax.set_ylabel('Actual outputs', fontsize=font_size, color='black')
ax.xaxis.set(ticks=range(10))
ax.yaxis.set(ticks=range(10))
ax.set_ylim(9.5, -0.5)
for i in range(10):
    for j in range(10):
        ax.text(j, i, cm[i, j], ha='center', va='center', color='white')
plt.show()

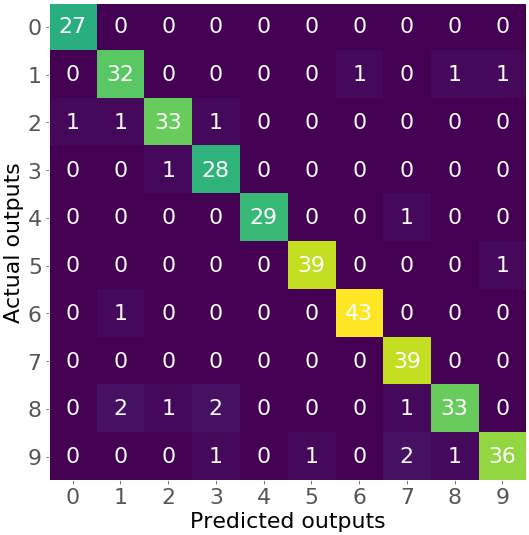
Приведенный выше код выдает следующую цифру матрицы путаницы:

Это тепловая карта, которая иллюстрирует матрицу путаницы с числами и цветами. Вы можете видеть, что оттенки фиолетового обозначают небольшие числа (например, 0, 1 или 2), в то время как зеленый и желтый показывают гораздо большие числа (27 и выше).

Числа на главной диагонали (27, 32, ..., 36) показывают количество правильных предсказаний из набора тестов. Например, есть 27 изображений с нулем, 32 изображения с единицей и так далее, которые правильно классифицированы. Другие цифры соответствуют неверным прогнозам. Например, цифра 1 в третьей строке и первом столбце показывает, что есть одно изображение с цифрой 2, ошибочно классифицированное как 0.

Наконец, вы можете получить отчет о классификации в виде строки или словаря с classification_report():

>>> print(classification_report(y_test, y_pred))
              precision    recall  f1-score   support

           0       0.96      1.00      0.98        27
           1       0.89      0.91      0.90        35
           2       0.94      0.92      0.93        36
           3       0.88      0.97      0.92        29
           4       1.00      0.97      0.98        30
           5       0.97      0.97      0.97        40
           6       0.98      0.98      0.98        44
           7       0.91      1.00      0.95        39
           8       0.94      0.85      0.89        39
           9       0.95      0.88      0.91        41

    accuracy                           0.94       360
   macro avg       0.94      0.94      0.94       360
weighted avg       0.94      0.94      0.94       360

В этом отчете представлена дополнительная информация, например, о поддержке и точности классификации каждой цифры.

За пределами логистической регрессии в Python

Логистическая регрессия - это фундаментальный метод классификации. Это относительно несложный линейный классификатор. Несмотря на его простоту и популярность, в некоторых случаях (особенно при использовании очень сложных моделей) логистическая регрессия работает неэффективно. В таких обстоятельствах вы можете использовать другие методы классификации:

• k-Ближайшие соседи
• Наивные байесовские классификаторы
• Методы опорных векторов
• Деревья решений
• Случайные леса
• Нейронные сети

К счастью, существует несколько комплексных библиотек Python для машинного обучения, которые реализуют эти методы. Например, пакет, который вы видели здесь в действии, scikit-learn, реализует все вышеупомянутые методы, за исключением нейронных сетей.

Для всех этих методов scikit-learn предлагает подходящие классы с такими методами, как model.fit(), model.predict_proba(), model.predict(), model.score(), и так далее. Вы можете комбинировать их с train_test_split(), confusion_matrix(), classification_report(), и другими.

Нейронные сети (включая глубокие нейронные сети) стали очень популярны для решения задач классификации. Библиотеки, такие как TensorFlow, PyTorch или Keras, предлагают подходящую, производительную и мощную поддержку для этих виды моделей.

Заключение

Теперь вы знаете, что такое логистическая регрессия и как ее можно реализовать для классификации с помощью Python. Вы использовали множество пакетов с открытым исходным кодом, включая NumPy, для работы с массивами и Matplotlib для визуализации результатов. Вы также использовали scikit-learn и StatsModels для создания, подгонки, оценки и применения моделей.

Как правило, логистическая регрессия в Python имеет простую и удобную для пользователя реализацию. Обычно она состоит из следующих шагов:

1. Импорт пакетов, функций и классов
2. Получите данные для работы и, при необходимости, преобразуйте их
3. Создайте классификационную модель и обработайте (или подогнав) ее под существующие данные
4. Оцените свою модель, чтобы убедиться в ее удовлетворительной производительности
5. Примените свою модель для составления прогнозов

Вы проделали долгий путь в понимании одной из важнейших областей машинного обучения!

Back to Top