Связанные списки в Python: Введение
Оглавление
- Понимание связанных списков
- Представляем коллекции.описание
- Создание Вашего собственного связанного списка
- Использование расширенных связанных списков
- Заключение
Смотрите сейчас, к этому уроку прилагается соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным руководством, чтобы углубить свое понимание: Работа со связанными списками в Python
Связанные списки похожи на менее известного родственника списков . Они не так популярны и не так круты, и вы, возможно, даже не помните их из своего курса по алгоритмам. Но в правильном контексте они могут действительно проявить себя.
Из этой статьи вы узнаете:
- Что такое связанные списки и когда их следует использовать
- Как использовать
collections.dequeдля всех ваших нужд в связанных списках - Как создавать свои собственные связанные списки
- Каковы другие типы связанных списков и для чего они могут быть использованы
Если вы хотите усовершенствовать свои навыки программирования для прохождения собеседования при приеме на работу или если вы хотите узнать больше о структурах данных Python помимо обычных словарей и списков, тогда вы обратились по адресу!
Вы можете ознакомиться с примерами из этого руководства, загрузив исходный код, доступный по ссылке ниже:
Получите исходный код: Нажмите здесь, чтобы получить исходный код, который вы будете использовать для ознакомления со связанными списками в этом руководстве.
Общие сведения о связанных списках
Связанные списки представляют собой упорядоченную коллекцию объектов. Так чем же они отличаются от обычных списков? Связанные списки отличаются от списков тем, как они хранят элементы в памяти. В то время как списки используют непрерывный блок памяти для хранения ссылок на свои данные, связанные списки хранят ссылки как часть своих собственных элементов.
Основные понятия
Прежде чем более подробно рассказывать о том, что такое связанные списки и как их можно использовать, вам следует сначала изучить их структуру. Каждый элемент связанного списка называется узлом, и каждый узел имеет два разных поля:
- Данные содержат значение, которое должно быть сохранено в узле.
- Далее содержит ссылку на следующий узел в списке.
Вот как выглядит типичный узел:
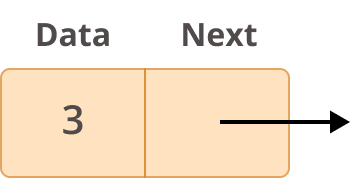 Узел
Узел
Связанный список представляет собой набор узлов. Первый узел называется head, и используется в качестве отправной точки для любой итерации по списку. Последний узел должен иметь ссылку next, указывающую на None чтобы определить конец списка. Вот как это выглядит:
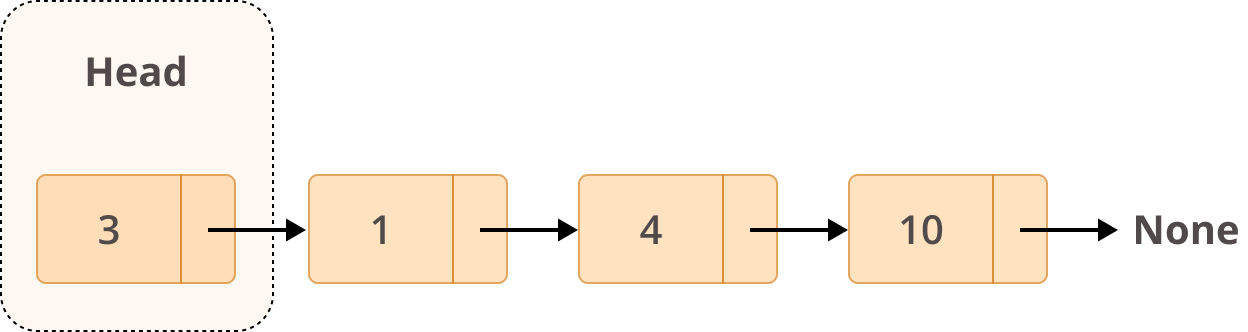 Связанный список
Связанный список
Теперь, когда вы знаете, как структурирован связанный список, вы готовы рассмотреть некоторые практические варианты его использования.
Практическое применение
Связанные списки служат различным целям в реальном мире. Они могут быть использованы для реализации (предупреждение о спойлере!) очереди или стеки, а также графики. Они также полезны для гораздо более сложных задач, таких как управление жизненным циклом приложения операционной системы.
Очереди или стеки
Очереди и стеки отличаются только способом извлечения элементов. Для очереди используется подход "Первый вход/первый выход" (FIFO). Это означает, что первый элемент, вставленный в список, является первым, который будет извлечен:
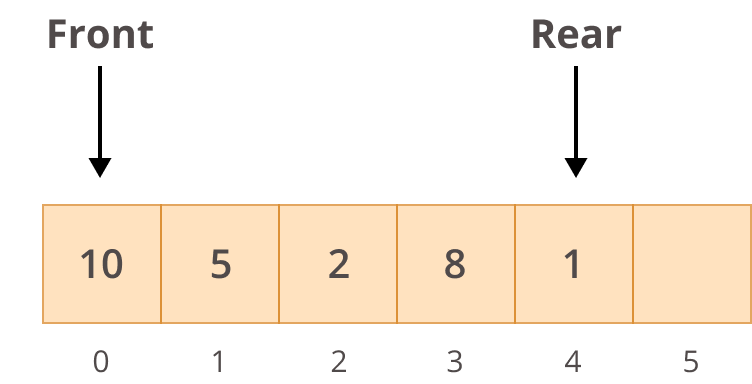 Очередь
Очередь
На диаграмме выше вы можете видеть передние и задние элементы очереди. Когда вы добавляете новые элементы в очередь, они перемещаются в конец очереди. Когда вы извлекаете элементы, они будут взяты из начала очереди.
Для стека используется подход Последний вход/первый выход (LIFO), означающий, что последний элемент, вставленный в список, извлекается первым:
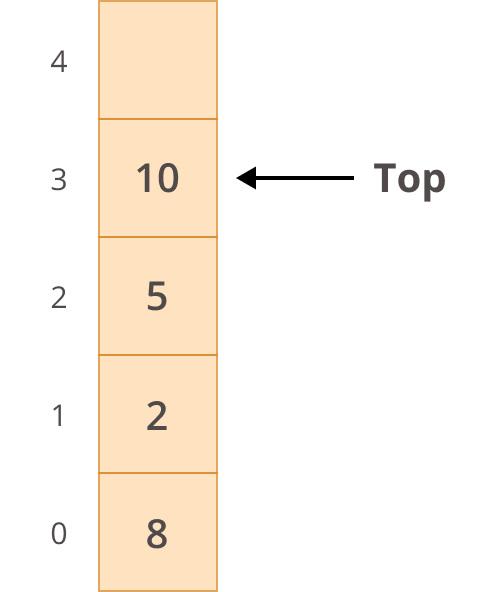 Стек
Стек
На приведенной выше диаграмме вы можете видеть, что первый элемент, вставленный в стек (индекс 0), находится внизу, а последний вставленный элемент - вверху. Поскольку в стеках используется подход LIFO, последний вставленный элемент (вверху) будет извлечен первым.
Благодаря способу вставки и извлечения элементов из границ очередей и стеков, связанные списки являются одним из наиболее удобных способов реализации этих структур данных. Далее в статье вы увидите примеры таких реализаций.
Графики
Графики могут использоваться для отображения взаимосвязей между объектами или для представления различных типов сетей. Например, визуальное представление графа — скажем, ориентированного ациклического графа (DAG) — может выглядеть следующим образом:
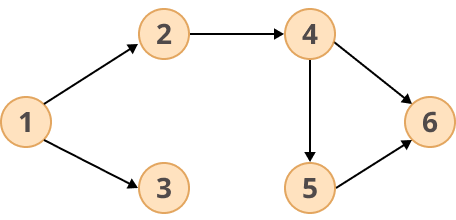 Направленный ациклический граф
Направленный ациклический граф
Существуют различные способы реализации графиков, подобных приведенному выше, но одним из наиболее распространенных является использование списка смежности. Список смежности - это, по сути, список связанных списков, в котором каждая вершина графа хранится рядом с набором связанных вершин:
| Vertex | Linked List of Vertices |
|---|---|
| 1 | 2 → 3 → None |
| 2 | 4 → None |
| 3 | None |
| 4 | 5 → 6 → None |
| 5 | 6 → None |
| 6 | None |
В таблице выше каждая вершина вашего графа указана в левом столбце. Правый столбец содержит ряд связанных списков, в которых хранятся другие вершины, связанные с соответствующей вершиной в левом столбце. Этот список смежности также может быть представлен в коде с помощью dict:
>>> graph = { ... 1: [2, 3, None], ... 2: [4, None], ... 3: [None], ... 4: [5, 6, None], ... 5: [6, None], ... 6: [None] ... }Ключами этого справочника являются исходные вершины, а значением для каждого ключа является список. Этот список обычно реализуется в виде связанного списка.
Примечание: В приведенном выше примере вы могли бы не сохранять значения
None, но мы сохранили их здесь для ясности и согласованности с последующими примерами.Как с точки зрения скорости, так и с точки зрения объема памяти, реализация графов с использованием списков смежности очень эффективна по сравнению, например, с матрицей смежности . Вот почему связанные списки так полезны для графической реализации.
Сравнение производительности: списки и связанные списки
В большинстве языков программирования существуют явные различия в способах хранения связанных списков и массивов в памяти. Однако в Python списки являются динамическими массивами. Это означает, что использование памяти как списками, так и связанными списками очень похоже.
Читать далее: Реализация динамических массивов в Python довольно интересна, и о ней определенно стоит прочитать. Обязательно посмотрите и используйте полученные знания, чтобы выделиться на следующей корпоративной вечеринке!
Поскольку разница в использовании памяти между списками и связанными списками настолько незначительна, что лучше сосредоточиться на различиях в производительности, когда речь заходит о временной сложности.
Вставка и удаление элементов
В Python вы можете вставлять элементы в список, используя
.insert()или.append(). Для удаления элементов из списка вы можете использовать их аналоги:.remove()и.pop().Основное различие между этими методами заключается в том, что вы используете
.insert()и.remove()для вставки или удаления элементов в определенной позиции списка, но вы используете.append()и.pop()только для вставки или удаления элементов в конце списка.Итак, кое-что, что вам нужно знать о списках Python, заключается в том, что вставка или удаление элементов, которые находятся , а не в конце списка, требует некоторого перемещения элементов в фоновом режиме, что усложняет операцию в Python. с точки зрения затраченного времени. Вы можете прочитать упомянутую выше статью о том, как списки реализованы в Python, чтобы лучше понять, как реализация
.insert(),.remove(),.append()и.pop()влияет на их производительность.Учитывая все это, даже если для вставки элементов в конец списка с помощью
.append()или.insert()потребуется постоянное время, O(1), когда вы пытаетесь вставить элемент ближе к списку или в его начало, средняя временная сложность будет расти вместе с размером списка: O(n).Связанные списки, с другой стороны, гораздо более просты, когда дело доходит до вставки и удаления элементов в начале или в конце списка, где их временная сложность всегда постоянна: O(1).
По этой причине связанные списки имеют преимущество в производительности перед обычными списками при реализации очереди (FIFO), в которой элементы непрерывно вставляются и удаляются в начале списка. Но они работают аналогично списку при реализации стека (LIFO), в котором элементы вставляются и удаляются в конце списка.
Извлечение элементов
Когда дело доходит до поиска элемента, списки выполняют гораздо лучше, чем связанные списки. Когда вы знаете, что элемент, который вы хотите открыть, списки могут выполнить эту операцию в О(1) Время. Попытка сделать то же самое со связанным списком займет O(n), потому что вам нужно просмотреть весь список, чтобы найти элемент.
Однако при поиске определенного элемента как списки, так и связанные списки выполняются очень похоже, с временной сложностью O(n). В обоих случаях вам нужно пройтись по всему списку, чтобы найти нужный элемент.
Представляем
collections.dequeВ Python в модуле
collectionsесть специальный объект, который вы можете использовать для связанных списков, называемый deque (произносится как “палуба”), что означает двусторонняя очередь.
collections.dequeиспользует реализацию связанного списка, в которой вы можете получать доступ, вставлять или удалять элементы из начала или конца списка с постоянной производительностью O(1) .Как использовать
collections.dequeСуществует довольно много методов, которые по умолчанию поставляются с
dequeобъектом. Однако в этой статье вы коснетесь лишь некоторых из них, в основном для добавления или удаления элементов.Сначала вам нужно создать связанный список. Для этого вы можете использовать следующий фрагмент кода с
deque:>>> from collections import deque >>> deque() deque([])Приведенный выше код создаст пустой связанный список. Если вы хотите заполнить его при создании, вы можете задать ему повторяемый в качестве входных данных:
>>> deque(['a','b','c']) deque(['a', 'b', 'c']) >>> deque('abc') deque(['a', 'b', 'c']) >>> deque([{'data': 'a'}, {'data': 'b'}]) deque([{'data': 'a'}, {'data': 'b'}])При инициализации объекта
dequeв качестве входных данных можно передать любую итерируемую строку, например, строку (также итерируемую) или список объектов.Теперь, когда вы знаете, как создать объект
deque, вы можете взаимодействовать с ним, добавляя или удаляя элементы. Вы можете создатьabcdeсвязанный список и добавить новый элементfвот так:>>> llist = deque("abcde") >>> llist deque(['a', 'b', 'c', 'd', 'e']) >>> llist.append("f") >>> llist deque(['a', 'b', 'c', 'd', 'e', 'f']) >>> llist.pop() 'f' >>> llist deque(['a', 'b', 'c', 'd', 'e'])И
append(), иpop()добавляют или удаляют элементы в правой части связанного списка. Однако вы также можете использоватьdequeдля быстрого добавления или удаления элементов в левой части списка илиhead:>>> llist.appendleft("z") >>> llist deque(['z', 'a', 'b', 'c', 'd', 'e']) >>> llist.popleft() 'z' >>> llist deque(['a', 'b', 'c', 'd', 'e'])Добавлять или удалять элементы из обоих концов списка довольно просто с помощью объекта
deque. Теперь вы готовы узнать, как использоватьcollections.dequeдля реализации очереди или стека.Как реализовать очереди и стеки
Как вы узнали выше, основное различие между очередью и стеком заключается в способе извлечения элементов из каждой из них. Далее вы узнаете, как использовать
collections.dequeдля реализации обеих структур данных.Очереди
При работе с очередями требуется добавлять значения в список (
enqueue), и, когда придет время, удалить элемент, который дольше всего находился в списке (dequeue). Например, представьте себе очередь в модном ресторане, где все места заняты. Если бы вы пытались внедрить справедливую систему рассадки гостей, то начали бы с создания очереди и добавления людей по мере их поступления:>>> from collections import deque >>> queue = deque() >>> queue deque([]) >>> queue.append("Mary") >>> queue.append("John") >>> queue.append("Susan") >>> queue deque(['Mary', 'John', 'Susan'])Теперь в очереди стоят Мэри, Джон и Сьюзен. Помните, что, поскольку очереди создаются по принципу FIFO, первый человек, который встал в очередь, должен первым выйти из нее.
Теперь представьте, что проходит некоторое время, и несколько столиков становятся доступными. На данном этапе вы хотите удалить людей из очереди в правильном порядке. Вот как бы вы это сделали:
>>> queue.popleft() 'Mary' >>> queue deque(['John', 'Susan']) >>> queue.popleft() 'John' >>> queue deque(['Susan'])Каждый раз, когда вы вызываете
popleft(), вы удаляете элемент head из связанного списка, имитируя реальную очередь.Стеки
Что, если бы вы захотели вместо создать стек? Что ж, идея более или менее такая же, как и в случае с очередью. Единственное отличие заключается в том, что в стеке используется подход LIFO, означающий, что последний элемент, который должен быть вставлен в стек, должен быть удален первым.
Представьте, что вы создаете функцию истории веб-браузера, в которой сохраняется каждая страница, которую посещает пользователь, чтобы он мог легко вернуться в прошлое. Предположим, что это действия, которые случайный пользователь выполняет в своем браузере:
- Посещений Веб-сайта Real Python
- Переход к Pandas: Как читать и записывать файлы
- Переход по ссылке для Чтения и записи CSV-файлов на Python
Если вы хотите отобразить это поведение в стеке, то вы могли бы сделать что-то вроде этого:
>>> from collections import deque >>> history = deque() >>> history.appendleft("https://realpython.com/") >>> history.appendleft("https://realpython.com/pandas-read-write-files/") >>> history.appendleft("https://realpython.com/python-csv/") >>> history deque(['https://realpython.com/python-csv/', 'https://realpython.com/pandas-read-write-files/', 'https://realpython.com/'])В этом примере вы создали пустой объект
history, и каждый раз, когда пользователь посещал новый сайт, вы добавляли его в свою переменнуюhistory, используяappendleft(). Это гарантировало, что каждый новый элемент будет добавлен вheadсвязанного списка.Теперь предположим, что после того, как пользователь прочитал обе статьи, он захотел вернуться на настоящую домашнюю страницу Python, чтобы выбрать новую статью для чтения. Зная, что у вас есть стек и вы хотите удалить элементы с помощью LIFO, вы могли бы сделать следующее:
>>> history.popleft() 'https://realpython.com/python-csv/' >>> history.popleft() 'https://realpython.com/pandas-read-write-files/' >>> history deque(['https://realpython.com/'])Вот и все! Используя
popleft(), вы удалили элементы изheadсвязанного списка, пока не достигли настоящей домашней страницы Python.Из приведенных выше примеров вы можете видеть, насколько полезным может быть наличие
collections.dequeв вашем наборе инструментов, поэтому обязательно используйте его в следующий раз, когда вам придется решать задачу на основе очереди или стека.Реализация Вашего собственного связанного списка
Теперь, когда вы знаете, как использовать
collections.dequeдля обработки связанных списков, вам может быть интересно, зачем вам вообще понадобилось создавать свой собственный связанный список в Python. Есть несколько причин сделать это:
- Отработка навыков работы с алгоритмами на Python
- Изучение теории структур данных
- Подготовка к собеседованиям при приеме на работу
Не стесняйтесь пропустить следующий раздел, если вас не интересует что-либо из вышеперечисленного, или если вы уже успешно реализовали свой собственный связанный список в Python. В противном случае, пришло время реализовать несколько связанных списков!
Как создать связанный список
Перво-наперво создайте класс, который будет представлять ваш связанный список:
class LinkedList: def __init__(self): self.head = NoneЕдинственная информация, которую вам нужно сохранить для связанного списка, - это то, с чего начинается список (
headсписка). Затем создайте другой класс для представления каждого узла связанного списка:class Node: def __init__(self, data): self.data = data self.next = NoneВ приведенном выше определении класса вы можете увидеть два основных элемента каждого отдельного узла:
dataиnext. Вы также можете добавить__repr__к обоим классам, чтобы иметь более удобное представление объектов:class Node: def __init__(self, data): self.data = data self.next = None def __repr__(self): return self.data class LinkedList: def __init__(self): self.head = None def __repr__(self): node = self.head nodes = [] while node is not None: nodes.append(node.data) node = node.next nodes.append("None") return " -> ".join(nodes)Взгляните на пример использования вышеуказанных классов для быстрого создания связанного списка с тремя узлами:
>>> llist = LinkedList() >>> llist None >>> first_node = Node("a") >>> llist.head = first_node >>> llist a -> None >>> second_node = Node("b") >>> third_node = Node("c") >>> first_node.next = second_node >>> second_node.next = third_node >>> llist a -> b -> c -> NoneОпределив значения узлов
dataиnext, вы можете довольно быстро создать связанный список. Эти классыLinkedListиNodeявляются отправными точками для нашей реализации. С этого момента все внимание сосредоточено на расширении их функциональности.Вот небольшое изменение в
__init__()связанном списке, которое позволяет вам быстро создавать связанные списки с некоторыми данными:def __init__(self, nodes=None): self.head = None if nodes is not None: node = Node(data=nodes.pop(0)) self.head = node for elem in nodes: node.next = Node(data=elem) node = node.nextС внесенными выше изменениями создание связанных списков для использования в примерах, приведенных ниже, будет намного быстрее.
Как перейти по связанному списку
Одна из наиболее распространенных операций, которую вы будете выполнять со связанным списком, - это обход его. Обход означает прохождение по каждому отдельному узлу, начиная с
headсвязанного списка и заканчивая узлом, который имеет значениеnextравноеNone.Переход - это просто более причудливый способ сказать "итерация". Итак, имея это в виду, создайте
__iter__, чтобы добавить к связанным спискам то же поведение, которое вы ожидаете от обычного списка:def __iter__(self): node = self.head while node is not None: yield node node = node.nextОписанный выше метод просматривает список и выдает для каждого отдельного узла. Самое важное, что нужно помнить об этом
__iter__- это то, что вам всегда нужно проверять, что текущее значениеnodeне равноNone. Если это условие равноTrue, это означает, что вы достигли конца своего связанного списка.После получения текущего узла вы хотите перейти к следующему узлу в списке. Вот почему вы добавляете
node = node.next. Вот пример просмотра случайного списка и печати каждого узла:>>> llist = LinkedList(["a", "b", "c", "d", "e"]) >>> llist a -> b -> c -> d -> e -> None >>> for node in llist: ... print(node) a b c d eВ других статьях вы можете увидеть, что обход определен в определенном методе, называемом
traverse(). Однако использование встроенных методов Python для достижения указанного поведения делает реализацию этого связанного списка немного более питонической.Как вставить новый узел
Существуют различные способы вставки новых узлов в связанный список, каждый из которых имеет свою собственную реализацию и уровень сложности. Вот почему вы увидите, что они разделены на конкретные методы для вставки в начало, конец или между узлами списка.
Вставка в начале
Вставка нового узла в начало списка, вероятно, является наиболее простой вставкой, поскольку для этого вам не нужно проходить по всему списку. Все дело в том, чтобы создать новый узел и затем указать на него
headиз списка.Взгляните на следующую реализацию
add_first()для классаLinkedList:def add_first(self, node): node.next = self.head self.head = nodeВ приведенном выше примере вы устанавливаете
self.headв качестве ссылки наnextнового узла, чтобы новый узел указывал на старыйself.head. После этого вам нужно указать, что новыйheadв списке является вставленным узлом.Вот как это работает с примером списка:
>>> llist = LinkedList() >>> llist None >>> llist.add_first(Node("b")) >>> llist b -> None >>> llist.add_first(Node("a")) >>> llist a -> b -> NoneКак вы можете видеть,
add_first()всегда добавляет узел вheadсписка, даже если до этого список был пустым.Вставка в конце
Вставка нового узла в конец списка заставляет вас сначала просмотреть весь связанный список и добавить новый узел, когда вы дойдете до конца. Вы не можете просто добавить в конец, как в случае с обычным списком, потому что в связанном списке вы не знаете, какой узел является последним.
Вот пример реализации функции для вставки узла в конец связанного списка:
def add_last(self, node): if self.head is None: self.head = node return for current_node in self: pass current_node.next = nodeСначала вы хотите просмотреть весь список, пока не дойдете до конца (то есть пока цикл
forне вызовет исключениеStopIteration). Затем вы хотите установитьcurrent_nodeв качестве последнего узла в списке. Наконец, вы хотите добавить новый узел в качестве значенияnextэтогоcurrent_node.Вот пример
add_last()в действии:>>> llist = LinkedList(["a", "b", "c", "d"]) >>> llist a -> b -> c -> d -> None >>> llist.add_last(Node("e")) >>> llist a -> b -> c -> d -> e -> None >>> llist.add_last(Node("f")) >>> llist a -> b -> c -> d -> e -> f -> NoneВ приведенном выше коде вы начинаете с создания списка с четырьмя значениями (
a,b,c, иd). Затем, когда вы добавляете новые узлы с помощьюadd_last(), вы можете видеть, что узлы всегда добавляются в конец списка.Вставка между двумя Узлами
Вставка между двумя узлами добавляет еще один уровень сложности к и без того сложным вставкам связанного списка, поскольку вы можете использовать два разных подхода:
- Вставка после существующего узла
- Вставка перед существующим узлом
Может показаться странным разбивать их на два метода, но связанные списки ведут себя иначе, чем обычные списки, и для каждого случая требуется отдельная реализация.
Вот метод, который добавляет узел после существующего узла с определенным значением данных:
def add_after(self, target_node_data, new_node): if self.head is None: raise Exception("List is empty") for node in self: if node.data == target_node_data: new_node.next = node.next node.next = new_node return raise Exception("Node with data '%s' not found" % target_node_data)В приведенном выше коде вы просматриваете связанный список в поисках узла с данными, указывающими, куда вы хотите вставить новый узел. Когда вы найдете нужный узел, вы сразу же вставите новый узел после него и измените ссылку
next, чтобы сохранить согласованность списка.Исключение составляют только те случаи, когда список пуст, что делает невозможным вставку нового узла после существующего, или если список не содержит искомого значения. Вот несколько примеров того, как ведет себя
add_after():>>> llist = LinkedList() >>> llist.add_after("a", Node("b")) Exception: List is empty >>> llist = LinkedList(["a", "b", "c", "d"]) >>> llist a -> b -> c -> d -> None >>> llist.add_after("c", Node("cc")) >>> llist a -> b -> c -> cc -> d -> None >>> llist.add_after("f", Node("g")) Exception: Node with data 'f' not foundПопытка использовать
add_after()в пустом списке приводит к исключению. То же самое происходит, когда вы пытаетесь добавить после несуществующего узла. Все остальное работает так, как ожидалось.Теперь, если вы хотите реализовать
add_before(), то это будет выглядеть примерно так:1def add_before(self, target_node_data, new_node): 2 if self.head is None: 3 raise Exception("List is empty") 4 5 if self.head.data == target_node_data: 6 return self.add_first(new_node) 7 8 prev_node = self.head 9 for node in self: 10 if node.data == target_node_data: 11 prev_node.next = new_node 12 new_node.next = node 13 return 14 prev_node = node 15 16 raise Exception("Node with data '%s' not found" % target_node_data)Есть несколько вещей, которые следует иметь в виду при реализации вышеизложенного. Во-первых, как и в случае с
add_after(), вы хотите убедиться, что создаете исключение, если связанный список пуст (строка 2) или искомый узел отсутствует (строка 16).Во-вторых, если вы пытаетесь добавить новый узел перед началом списка (строка 5), то вы можете повторно использовать
add_first(), потому что вставляемый узел будет новымheadв списке.Наконец, в любом другом случае (строка 9) вы должны отслеживать последний проверенный узел, используя переменную
prev_node. Затем, когда вы найдете целевой узел, вы можете использовать эту переменнуюprev_nodeдля изменения значенийnext.Еще раз повторю, что один пример стоит тысячи слов:
>>> llist = LinkedList() >>> llist.add_before("a", Node("a")) Exception: List is empty >>> llist = LinkedList(["b", "c"]) >>> llist b -> c -> None >>> llist.add_before("b", Node("a")) >>> llist a -> b -> c -> None >>> llist.add_before("b", Node("aa")) >>> llist.add_before("c", Node("bb")) >>> llist a -> aa -> b -> bb -> c -> None >>> llist.add_before("n", Node("m")) Exception: Node with data 'n' not foundС помощью
add_before()У вас теперь есть все необходимые методы для вставки узлов в любое удобное для вас место в вашем списке.Как удалить узел
Чтобы удалить узел из связанного списка, вам сначала нужно просмотреть список, пока вы не найдете нужный узел. Как только вы найдете целевой узел, вам нужно связать его предыдущий и следующий узлы. Это повторное связывание удаляет целевой узел из списка.
Это означает, что вам нужно отслеживать предыдущий узел при просмотре списка. Взгляните на пример реализации:
1def remove_node(self, target_node_data): 2 if self.head is None: 3 raise Exception("List is empty") 4 5 if self.head.data == target_node_data: 6 self.head = self.head.next 7 return 8 9 previous_node = self.head 10 for node in self: 11 if node.data == target_node_data: 12 previous_node.next = node.next 13 return 14 previous_node = node 15 16 raise Exception("Node with data '%s' not found" % target_node_data)В приведенном выше коде вы сначала проверяете, что ваш список не пуст (строка 2). Если это так, то вы создаете исключение. После этого вы проверяете, является ли удаляемый узел текущим
headв списке (строка 5). Если это так, то вы хотите, чтобы следующий узел в списке стал новым.head.Если ничего из вышеперечисленного не происходит, вы начинаете просматривать список в поисках узла, который нужно удалить (строка 10). Если вы его найдете, то вам нужно обновить его предыдущий узел, чтобы он указывал на следующий узел, автоматически удаляя найденный узел из списка. Наконец, если вы просматриваете весь список, не находя узел, который нужно удалить (строка 16), то вы создаете исключение.
Обратите внимание, что в приведенном выше коде вы используете
previous_nodeдля отслеживания предыдущего узла. Это гарантирует, что весь процесс будет намного проще, когда вы найдете нужный узел для удаления.Вот пример использования списка:
>>> llist = LinkedList() >>> llist.remove_node("a") Exception: List is empty >>> llist = LinkedList(["a", "b", "c", "d", "e"]) >>> llist a -> b -> c -> d -> e -> None >>> llist.remove_node("a") >>> llist b -> c -> d -> e -> None >>> llist.remove_node("e") >>> llist b -> c -> d -> None >>> llist.remove_node("c") >>> llist b -> d -> None >>> llist.remove_node("a") Exception: Node with data 'a' not foundВот и все! Теперь вы знаете, как реализовать связанный список и все основные методы обхода, вставки и удаления узлов. Если вы довольны тем, что узнали, и хотите большего, тогда смело выбирайте одно из следующих заданий:
- Создайте метод для извлечения элемента из определенной позиции:
get(i)или дажеllist[i].- Создайте метод для изменения связанного списка:
llist.reverse().- Создайте
Queue()объект, наследующий связанный список из этой статьи, с помощью методовenqueue()иdequeue().Помимо того, что это отличная практика, самостоятельное выполнение некоторых дополнительных заданий - эффективный способ усвоить все полученные знания. Если вы хотите начать с повторного использования всего исходного кода из этой статьи, то вы можете скачать все, что вам нужно, по ссылке ниже:
Получите исходный код: Нажмите здесь, чтобы получить исходный код, который вы будете использовать для ознакомления со связанными списками в этом руководстве.
Использование расширенных связанных списков
До сих пор вы изучали особый тип связанных списков, который называется односвязные списки. Но есть и другие типы связанных списков, которые можно использовать для несколько иных целей.
Как использовать двусвязные списки
Двусвязные списки отличаются от односвязных списков тем, что на них есть две ссылки:
- Поле
previousссылается на предыдущий узел.- Поле
nextссылается на следующий узел.Конечный результат выглядит следующим образом:
Узел (двусвязный список)
Если вы хотите реализовать описанное выше, то вы могли бы внести некоторые изменения в свой существующий класс
Node, чтобы включить полеprevious:class Node: def __init__(self, data): self.data = data self.next = None self.previous = NoneТакая реализация позволила бы вам перемещаться по списку в обоих направлениях вместо того, чтобы перемещаться только с помощью
next. Вы можете использоватьnextдля перехода вперед иpreviousдля перехода назад.С точки зрения структуры, вот как должен выглядеть двусвязный список:
Двусвязный список
Ранее вы узнали, что
collections.dequeиспользует связанный список как часть своей структуры данных. Это такой связанный список, который он использует. При использовании двусвязных списковdequeможно вставлять или удалять элементы с обоих концов очереди с постоянной производительностью O(1).Как использовать циклически связанные списки
Циклически связанные списки - это тип связанного списка, в котором последний узел указывает на
headсписка вместо того, чтобы указывать наNone. Именно это делает их циклическими. Циклически связанные списки имеют довольно много интересных вариантов использования:
- Выполнение хода каждого игрока в многопользовательской игре
- Управление жизненным циклом приложения данной операционной системы
- Реализация кучи Фибоначчи
Вот как выглядит круговой связанный список:
Круговой связанный список
Одним из преимуществ циклически связанных списков является то, что вы можете просмотреть весь список, начиная с любого узла. Поскольку последний узел указывает на
headв списке, вам нужно убедиться, что вы прекратили обход, когда достигли начальной точки. В противном случае вы окажетесь в бесконечном цикле.С точки зрения реализации циклически связанные списки очень похожи на односвязные списки. Единственное отличие заключается в том, что вы можете определить начальную точку при просмотре списка:
class CircularLinkedList: def __init__(self): self.head = None def traverse(self, starting_point=None): if starting_point is None: starting_point = self.head node = starting_point while node is not None and (node.next != starting_point): yield node node = node.next yield node def print_list(self, starting_point=None): nodes = [] for node in self.traverse(starting_point): nodes.append(str(node)) print(" -> ".join(nodes))При обходе списка теперь используется дополнительный аргумент
starting_point, который используется для определения начала и (поскольку список является циклическим) конца итерационного процесса. Кроме того, большая часть кода такая же, как и в нашем классеLinkedList.В заключение приведем последний пример, посмотрим, как ведет себя этот новый тип списка, когда вы вводите в него некоторые данные:
>>> circular_llist = CircularLinkedList() >>> circular_llist.print_list() None >>> a = Node("a") >>> b = Node("b") >>> c = Node("c") >>> d = Node("d") >>> a.next = b >>> b.next = c >>> c.next = d >>> d.next = a >>> circular_llist.head = a >>> circular_llist.print_list() a -> b -> c -> d >>> circular_llist.print_list(b) b -> c -> d -> a >>> circular_llist.print_list(d) d -> a -> b -> cВот и все! Вы заметите, что при просмотре списка у вас больше нет
None. Это потому, что у круглого списка нет определенного конца. Вы также можете видеть, что при выборе разных начальных узлов один и тот же список будет отображаться несколько по-разному.Заключение
Из этой статьи вы узнали немало нового! Наиболее важными из них являются:
- Что такое связанные списки и когда их следует использовать
- Как использовать
collections.dequeдля реализации очередей и стеков- Как реализовать свой собственный связанный список и классы узлов, а также соответствующие методы
- Что такое другие типы связанных списков и для чего их можно использовать
Если вы хотите узнать больше о связанных списках, ознакомьтесь с Публикацией Вайдехи Джоши в Medium, в которой содержится наглядное объяснение. Если вас интересует более подробное руководство, то статья в Википедии довольно подробная. Наконец, если вам интересно узнать о причинах, лежащих в основе текущей реализации
collections.deque, ознакомьтесь с статьей Раймонда Хеттингера.Вы можете загрузить исходный код, используемый в этом руководстве, перейдя по следующей ссылке:
Получите исходный код: Нажмите здесь, чтобы получить исходный код, который вы будете использовать для ознакомления со связанными списками в этом руководстве.
Не стесняйтесь оставлять любые вопросы или комментарии ниже. Приятного чтения!
<статус завершения article-slug="связанные списки-python" class="btn-group mb-0" data-api-article-bookmark-url="/api/v1/статьи/связанные списки-python/bookmark/" data-api-article-завершение-статус-url="/api/версия 1/статьи/связанные списки-python/завершение_статуса/"> <кнопка поделиться bluesky-text="Интересная статья на #Python от @realpython.com :" email-body="Ознакомьтесь с этой статьей о Python:%0A%0связанные списки в Python: введение" email-subject="Статья о Python для вас" twitter-text="Интересная статья о #Python от @realpython:" url="https://realpython.com/linked-lists-python /" url-title="Связанные списки в Python: введение">Смотрите сейчас, к этому уроку прилагается соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным руководством, чтобы углубить свое понимание: Работа со связанными списками в Python
Back to Top