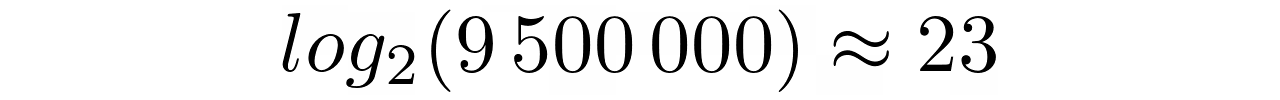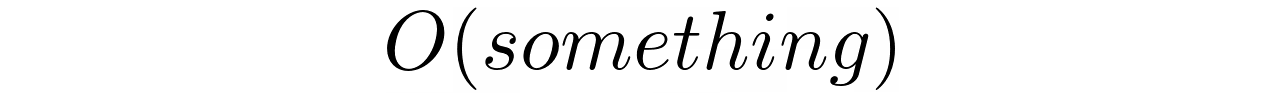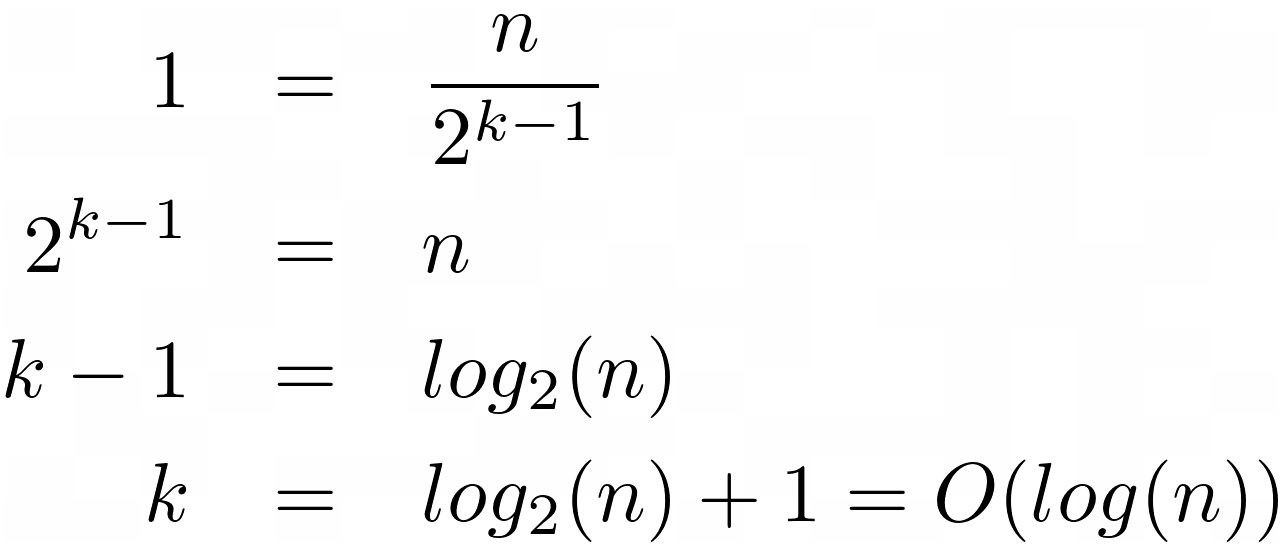Как выполнить двоичный поиск в Python

Оглавление

• Сравнительный анализ
  • Скачать IMDb
  • Чтение значений, разделенных табуляцией
  • Измерьте время выполнения
• Понимание алгоритмов поиска
  • Случайный поиск
  • Линейный поиск
  • Бинарный поиск
  • Поиск на основе хэша
• Использование модуля деления пополам
  • Поиск элемента
  • Вставка нового элемента
• Реализация бинарного поиска в Python
  • Итеративно
  • Рекурсивно
• Освещение сложных деталей
  • Переполнение целых чисел
  • Переполнение стека
  • Повторяющиеся элементы
  • Округление с плавающей запятой
• Анализ пространственно-временной сложности бинарного поиска
  • Пространственно-временная сложность
  • Обозначение большой буквы "О"
  • Сложность бинарного поиска
• Заключение

Бинарный поиск - классический алгоритм в информатике. Он часто используется на конкурсах по программированию и технических собеседованиях. Реализация бинарного поиска оказывается сложной задачей, даже если вы понимаете концепцию. Если вам не интересно или у вас нет конкретного задания, вы всегда должны использовать существующие библиотеки для выполнения бинарного поиска на Python или любом другом языке.

В этом руководстве вы узнаете, как:

• Используйте модуль bisect для выполнения бинарного поиска в Python
• Реализуйте бинарный поиск в Python как рекурсивно, так и итеративно
• Распознавать и исправлять дефекты в реализации бинарного поиска на Python
• Проанализируйте пространственно-временную сложность алгоритма бинарного поиска
• Поиск выполняется даже быстрее, чем бинарный поиск

В этом руководстве предполагается, что вы студент или программист среднего уровня с интересом к алгоритмам и данным структуры. По крайней мере, вы должны быть знакомы со встроенными в Python типами данных, такими как списки и кортежи. Кроме того, необходимо некоторое знакомство с рекурсией, классов, классов данных и лямбда-выражения помогут вам лучше понять концепции, с которыми вы познакомитесь в этом руководстве.

Ниже вы найдете ссылку на пример кода, который вы увидите в этом руководстве, для запуска которого требуется Python 3.7 или более поздней версии:

Получите пример кода: Нажмите здесь, чтобы получить пример кода, который вы будете использовать для изучения бинарного поиска в Python в этом руководстве.

Сравнительный анализ

В следующем разделе этого руководства вы будете использовать подмножество Базы данных фильмов Интернета (IMDb) для сравнения производительности нескольких алгоритмов поиска. Этот набор данных доступен бесплатно для личного и некоммерческого использования. Он распространяется в виде набора сжатых значений, разделенных табуляцией (TSV) файлов, которые ежедневно обновляются.

Чтобы упростить вам жизнь, вы можете использовать скрипт на Python, включенный в пример кода. Он автоматически найдет соответствующий файл с IMDb, распакует его и извлечет интересные фрагменты:

$ python download_imdb.py
Fetching data from IMDb...
Created "names.txt" and "sorted_names.txt"

Имейте в виду, что при этом будет загружено и извлечено приблизительно 600 МБ данных, а также будут созданы два дополнительных файла, которые будут примерно вдвое меньше по размеру. Загрузка, а также обработка этих данных могут занять минуту или две.

Скачать IMDb

, чтобы вручную получить информацию, перейдите в свой веб-браузер до https://datasets.imdbws.com/ и захватить файл name.basics.tsv.gz, который содержит записи актеров, режиссеров, писателей, и так далее. Когда вы распакуете файл, вы увидите следующее содержимое:

nconst     primaryName      birthYear  deathYear  (...)
nm0000001  Fred Astaire     1899       1987       (...)
nm0000002  Lauren Bacall    1924       2014       (...)
nm0000003  Brigitte Bardot  1934       \N         (...)
nm0000004  John Belushi     1949       1982       (...)

В нем есть заголовок с именами столбцов в первой строке, за которыми следуют записи данных в каждой из последующих строк. Каждая запись содержит уникальный идентификатор, полное имя, год рождения и несколько других атрибутов. Все они разделены символом табуляции.

В файле миллионы записей, поэтому не пытайтесь открыть файл в обычном текстовом редакторе, чтобы избежать сбоя в работе компьютера. Даже в специализированных программах, таких как электронные таблицы, могут возникнуть проблемы с его открытием. Вместо этого вы можете воспользоваться преимуществами высокопроизводительного средства просмотра таблиц данных, включенного, например, в JupyterLab.

Считывание значений, разделенных табуляцией

Существует несколько способов анализа TSV-файла. Например, вы можете прочитать его с помощью Pandas, использовать специальное приложение или воспользоваться несколькими инструментами командной строки. Однако рекомендуется использовать простой скрипт на Python, включенный в пример кода.

Примечание: Как правило, вам следует избегать разбора файлов вручную, поскольку вы можете упустить из виду крайние случаи. Например, в одном из полей разделительный символ табуляции можно было бы использовать буквально в кавычках, что привело бы к сокращению количества столбцов. По возможности постарайтесь найти соответствующий модуль в стандартной библиотеке или в надежном стороннем приложении.

В конечном счете, вы хотите получить в свое распоряжение два текстовых файла:

1. names.txt
2. sorted_names.txt

Один из них будет содержать список имен, полученных путем вырезания второго столбца из исходного TSV-файла:

Fred Astaire
Lauren Bacall
Brigitte Bardot
John Belushi
Ingmar Bergman
...

Второй будет отсортированной версией этого.

Как только оба файла будут готовы, вы можете загрузить их в Python, используя эту функцию:

def load_names(path):
    with open(path) as text_file:
        return text_file.read().splitlines()

names = load_names('names.txt')
sorted_names = load_names('sorted_names.txt')

Этот код возвращает список имен, извлеченных из данного файла. Обратите внимание, что вызов .splitlines() для результирующей строки удаляет завершающий символ новой строки из каждой строки. В качестве альтернативы вы могли бы вызвать text_file.readlines(), но это привело бы к появлению ненужных новых строк.

Измерьте время выполнения

Чтобы оценить производительность конкретного алгоритма, вы можете сравнить время его выполнения с набором данных IMDb. Обычно это делается с помощью встроенных модулей time или timeit, которые полезны для синхронизации блока кода.

Вы также могли бы определить пользовательский декоратор для определения времени выполнения функции, если бы захотели. В приведенном примере кода используется time.perf_counter_ns(),, введенный в Python 3.7, поскольку он обеспечивает высокую точность в наносекундах.

Понимание алгоритмов поиска

Поиск вездесущ и лежит в основе информатики. Вы, вероятно, сегодня самостоятельно выполнили несколько поисковых запросов в Интернете, но задумывались ли вы когда-нибудь, что на самом деле означает поиск?

Алгоритмы поиска могут принимать множество различных форм. Например, вы можете:

• Выполните полнотекстовый поиск
• Сопоставьте строки с помощью нечеткого поиска
• Найдите кратчайший путь в графе
• Запросить базу данных
• Найти минимальное или максимальное значение

В этом руководстве вы узнаете о поиске элемента в отсортированном списке элементов, например, в телефонной книге. При поиске такого элемента у вас может возникнуть один из следующих вопросов:

Вопрос	Ответ
Он там есть?	Да
Где это?	На 42-й странице
Какой из них?	Человек по имени Джон Доу

Ответ на первый вопрос подсказывает, присутствует ли элемент в коллекции. Он всегда содержит либо true, либо false. Второй ответ - это расположение элемента в коллекции, который может быть недоступен, если этот элемент отсутствовал. Наконец, третий ответ - это сам элемент или его отсутствие.

Примечание: Иногда может быть более одного правильного ответа из-за повторяющихся или похожих пунктов. Например, если у вас есть несколько контактов с одинаковыми именами, все они будут соответствовать вашим критериям поиска. В других случаях ответ может быть приблизительным или отсутствовать вообще.

В наиболее распространенном случае вы будете выполнять поиск по значению, которое сравнивает элементы в коллекции с тем, который вы указали в качестве ссылки. Другими словами, критерием поиска является весь элемент, такой как число, строка или объект, например человек. Даже малейшее различие между двумя сравниваемыми элементами не приведет к совпадению.

С другой стороны, вы можете уточнить критерии поиска, выбрав какое-либо свойство элемента, например фамилию человека. Это называется поиск по ключу, поскольку вы выбираете один или несколько атрибутов для сравнения. Прежде чем вы погрузитесь в бинарный поиск в Python, давайте кратко рассмотрим другие алгоритмы поиска, чтобы получить более полную картину и понять, как они работают.

Случайный поиск

Как бы вы могли поискать что-нибудь в своем рюкзаке? Вы можете просто запустить в него руку, выбрать предмет наугад и посмотреть, тот ли это, который вы хотели. Если вам не повезло, то вы кладете предмет на место, промываете и повторяете процедуру. Этот пример - хороший способ понять случайный поиск, который является одним из наименее эффективных алгоритмов поиска. Неэффективность этого подхода проистекает из того факта, что вы рискуете несколько раз неправильно выбрать одну и ту же вещь.

Примечание: Как ни странно, эта стратегия теоретически могла бы быть наиболее эффективной, если бы вы были очень повезло или в коллекции было небольшое количество элементов.

Фундаментальный принцип этого алгоритма может быть выражен следующим фрагментом кода на Python:

import random

def find(elements, value):
    while True:
        random_element = random.choice(elements)
        if random_element == value:
            return random_element

Функция выполняет цикл до тех пор, пока какой-либо элемент, выбранный случайным образом из , не совпадет со значением, заданным в качестве входных данных. Однако это не очень полезно, поскольку функция возвращает либо None неявно, либо то же значение, которое она уже получила в параметре.

Обратите внимание, что эта функция никогда не завершается из-за пропущенных значений. Вы можете найти полную реализацию, которая учитывает такие сложные случаи, в примере кода, доступном для скачивания по ссылке ниже:

Получите пример кода: Нажмите здесь, чтобы получить пример кода, который вы будете использовать для изучения бинарного поиска в Python в этом руководстве.

Для микроскопических наборов данных алгоритм случайного поиска, по-видимому, выполняет свою работу достаточно быстро:

>>> from search.random import *  # Sample code to download
>>> fruits = ['orange', 'plum', 'banana', 'apple']
>>> contains(fruits, 'banana')
True
>>> find_index(fruits, 'banana')
2
>>> find(fruits, key=len, value=4)
'plum'

Однако представьте, что вам приходится выполнять подобный поиск в миллионах элементов! Вот краткое описание теста производительности, который был проведен на основе набора данных IMDb:

Search Term	Element Index	Best Time	Average Time	Worst Time
Fred Astaire	0	0.74s	21.69s	43.16s
Alicia Monica	4,500,000	1.02s	26.17s	66.34s
Baoyin Liu	9,500,000	0.11s	17.41s	51.03s
missing	N/A	5m 16s	5m 40s	5m 54s

Уникальные элементы в разных ячейках памяти были специально подобраны, чтобы избежать предвзятости. Поиск по каждому термину проводился десять раз, чтобы учесть случайность алгоритма и другие факторы, такие как сбор мусора или системные процессы, выполняющиеся в фоновом режиме.

Примечание: Если вы хотите провести этот эксперимент самостоятельно, то обратитесь к инструкциям, приведенным во введении к этому руководству. Чтобы измерить производительность вашего кода, вы можете использовать встроенные модули time и timeit { или вы можете настроить время выполнения функций с помощью пользовательского декоратора.

Алгоритм обладает недетерминированной производительностью. Хотя среднее время нахождения элемента не зависит от его местонахождения, наилучшее и наихудшее время различаются на два-три порядка. Он также страдает от несогласованного поведения. Рассмотрите возможность создания коллекции элементов, содержащих несколько дубликатов. Поскольку алгоритм выбирает элементы случайным образом, при последующих запусках он неизбежно вернет разные копии.

Как вы можете это улучшить? Один из способов решения обеих проблем одновременно - использовать линейный поиск .

Линейный поиск

Когда вы решаете, что приготовить на обед, вы, возможно, хаотично просматриваете меню, пока что-то не привлечет ваше внимание. В качестве альтернативы, вы можете использовать более систематический подход, просматривая меню сверху вниз и тщательно изучая каждый пункт в последовательности . В двух словах, это линейный поиск. Чтобы реализовать это на Python, вы могли бы использовать enumerate() элементы для отслеживания индекса текущего элемента:

def find_index(elements, value):
    for index, element in enumerate(elements):
        if element == value:
            return index

Функция выполняет цикл по набору элементов в заранее определенном и согласованном порядке. Она останавливается, когда элемент найден или когда больше нет элементов для проверки. Эта стратегия гарантирует, что ни один элемент не будет посещен более одного раза, потому что вы проходите по ним в порядке index.

Давайте посмотрим, насколько хорошо линейный поиск справляется с набором данных IMDb, который вы использовали ранее:

Search Term	Element Index	Best Time	Average Time	Worst Time
Fred Astaire	0	491ns	1.17µs	6.1µs
Alicia Monica	4,500,000	0.37s	0.38s	0.39s
Baoyin Liu	9,500,000	0.77s	0.79s	0.82s
missing	N/A	0.79s	0.81s	0.83s

Время поиска отдельного элемента практически не отличается. Среднее время поиска практически одинаково как для лучшего, так и для худшего элемента. Поскольку элементы всегда просматриваются в одном и том же порядке, количество сравнений, необходимых для поиска одного и того же элемента, не меняется.

Однако время поиска увеличивается с увеличением индекса элемента в коллекции. Чем дальше элемент находится от начала списка, тем больше сравнений приходится выполнять. В худшем случае, когда элемент отсутствует, необходимо проверить всю коллекцию, чтобы дать однозначный ответ.

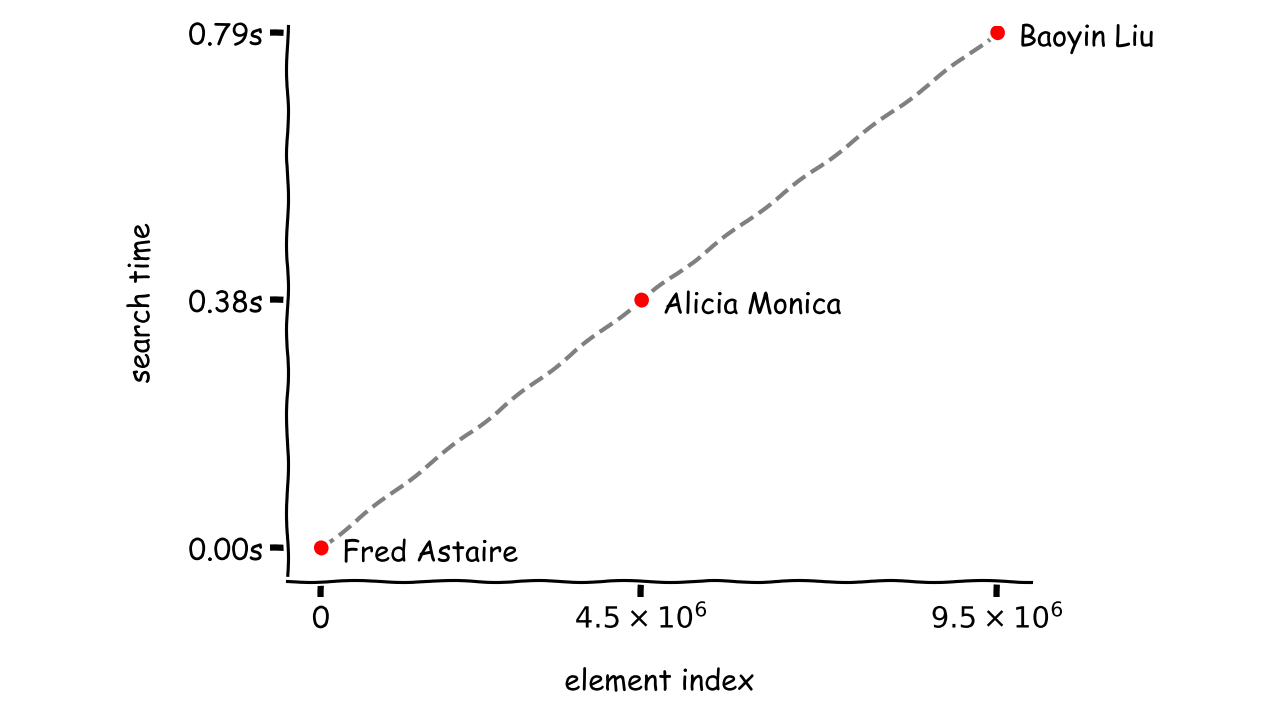
Когда вы спроецируете экспериментальные данные на график и соедините точки, вы сразу увидите взаимосвязь между местоположением элемента и временем, затрачиваемым на его поиск:

Все выборки лежат на прямой и могут быть описаны линейной функцией, отсюда и название алгоритма. Можно предположить, что в среднем время, необходимое для поиска любого элемента с помощью линейного поиска, будет пропорционально количеству всех элементов в коллекции. Они плохо масштабируются по мере увеличения объема данных для поиска.

Например, биометрические сканеры, доступные в некоторых аэропортах, не смогли бы распознать пассажиров за считанные секунды, если бы они были реализованы с использованием линейного поиска. С другой стороны, алгоритм линейного поиска может быть хорошим выбором для небольших наборов данных, поскольку он не требует предварительной обработки данных. В таком случае преимущества предварительной обработки не окупят ее затрат.

Python уже поставляется с линейным поиском, так что нет смысла писать его самостоятельно. Структура данных list, например, предоставляет метод, который возвращает индекс элемента или вызывает исключение в противном случае:

>>> fruits = ['orange', 'plum', 'banana', 'apple']
>>> fruits.index('banana')
2
>>> fruits.index('blueberry')
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: 'blueberry' is not in list

это также может сказать вам, если элемент присутствует в коллекции, но не более обновления способ предполагает использование универсального in оператор:

>>> 'banana' in fruits
True
>>> 'blueberry' in fruits
False

Стоит отметить, что, несмотря на скрытое использование линейного поиска, эти встроенные функции и операторы выведут вашу реализацию из строя. Это потому, что они были написаны на чистом C, который компилируется в машинный код. Стандартный интерпретатор Python не подходит для этого, как бы вы ни старались.

Быстрый тест с помощью модуля timeit показывает, что реализация на Python может выполняться почти в десять раз медленнее, чем эквивалентная нативная реализация:

>>> import timeit
>>> from search.linear import contains
>>> fruits = ['orange', 'plum', 'banana', 'apple']
>>> timeit.timeit(lambda: contains(fruits, 'blueberry'))
1.8904765040024358
>>> timeit.timeit(lambda: 'blueberry' in fruits)
0.22473459799948614

Однако для достаточно больших наборов данных даже машинный код будет работать на пределе возможностей, и единственным решением будет переосмысление алгоритма.

Примечание: Оператор in не всегда выполняет линейный поиск. Например, когда вы используете его для set, вместо этого он выполняет поиск на основе хэша. Оператор может работать с любым повторяемым, включая tuple, list, set, dict, и str. Вы даже можете поддерживать с его помощью свои пользовательские классы, реализовав метод magic .__contains__() для определения базовой логики.

В реальной жизни обычно следует избегать линейного алгоритма поиска. Например, однажды я не смог зарегистрировать свою кошку в ветеринарной клинике, потому что их система постоянно давала сбои. Врач сказал мне, что в конечном итоге ему придется обновить свой компьютер, потому что при добавлении новых записей в базу данных он будет работать все медленнее и медленнее.

Помню, в тот момент я подумал про себя, что человек, написавший это программное обеспечение, явно не знал об алгоритме бинарного поиска !

Бинарный поиск

Слово двоичный обычно ассоциируется с числом 2. В данном контексте оно относится к разделению набора элементов на две половины и отбрасыванию одной из них на каждом шаге алгоритма. Это может значительно сократить количество сравнений, необходимых для поиска элемента. Но есть одна загвоздка — элементы в коллекции должны быть сначала отсортированы.

Идея, лежащая в основе этого, напоминает действия по поиску страницы в книге. Сначала вы обычно открываете книгу на совершенно случайной странице или, по крайней мере, на той, которая, по вашему мнению, находится близко к нужной странице.

Иногда вам удается найти нужную страницу с первой попытки. Однако, если номер страницы слишком мал, то вы знаете, что страница должна быть справа. Если при следующей попытке вы ошибетесь и номер текущей страницы окажется больше, чем номер страницы, которую вы ищете, то вы точно знаете, что она должна быть где-то посередине.

Вы повторяете процесс, но вместо того, чтобы выбирать страницу наугад, вы проверяете страницу, расположенную прямо в середине этого нового диапазона. Это сводит к минимуму количество попыток. Аналогичный подход можно использовать в игре на угадывание чисел . Если вы не слышали об этой игре, то можете поискать ее в Интернете и найти множество примеров, реализованных на Python.

Примечание: Иногда, если значения распределены равномерно, вы можете вычислить средний индекс с помощью линейной интерполяции вместо того, чтобы брать среднее значение. Этот вариант алгоритма потребует еще меньшего количества шагов.

Номера страниц, которые ограничивают диапазон страниц для поиска, называются нижняя граница и верхняя граница. При бинарном поиске вы обычно начинаете с первой страницы в качестве нижней границы, а последней страницы - в качестве верхней границы. Вы должны обновлять обе границы по мере продвижения. Например, если страница, на которую вы переходите, находится ниже, чем та, которую вы ищете, то это ваша новая нижняя граница.

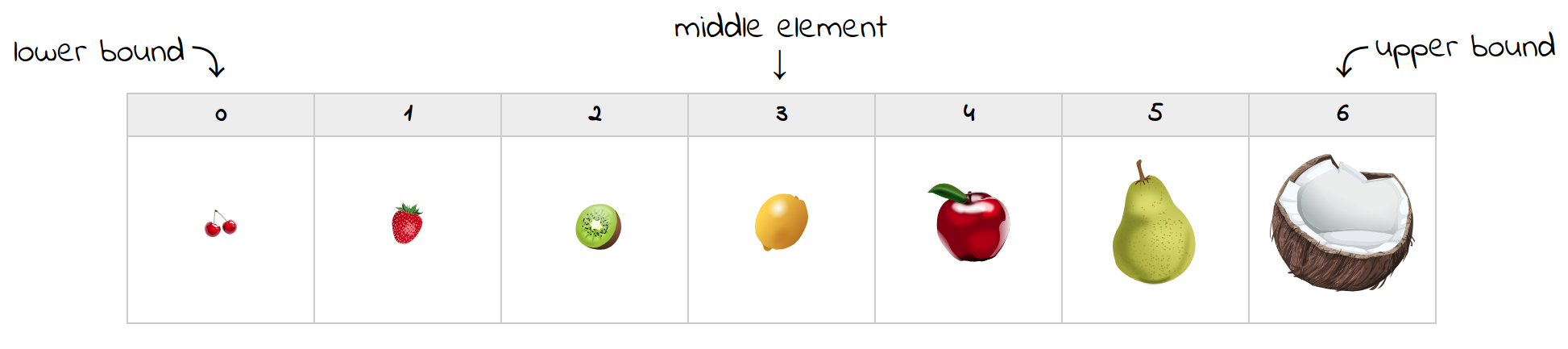
Допустим, вы искали клубнику в коллекции фруктов, отсортированных в порядке возрастания по размеру:

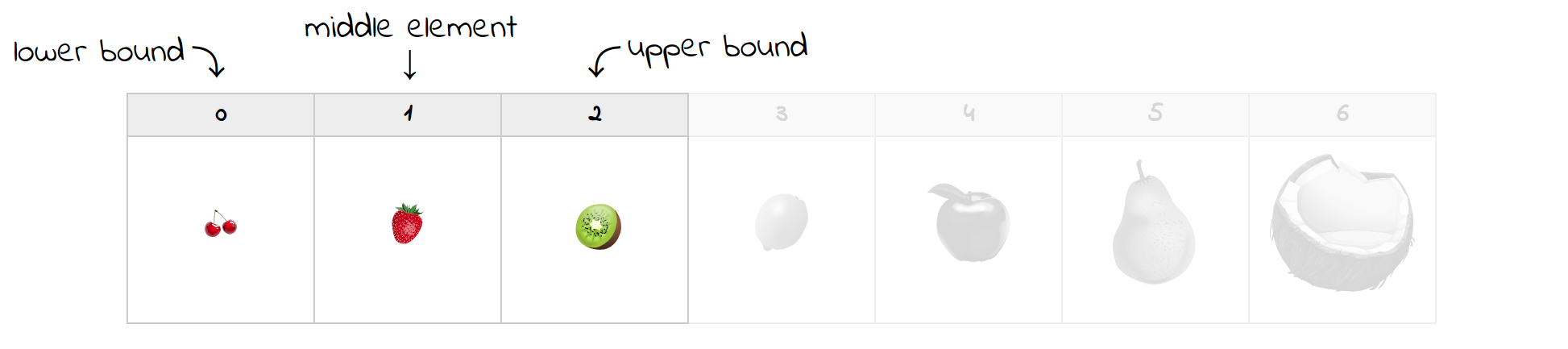
С первой попытки получается, что элемент в середине - это лимон. Поскольку он больше клубники, вы можете отбросить все элементы справа, включая лимон. Вы переместите верхнюю границу в новое положение и обновите средний индекс:

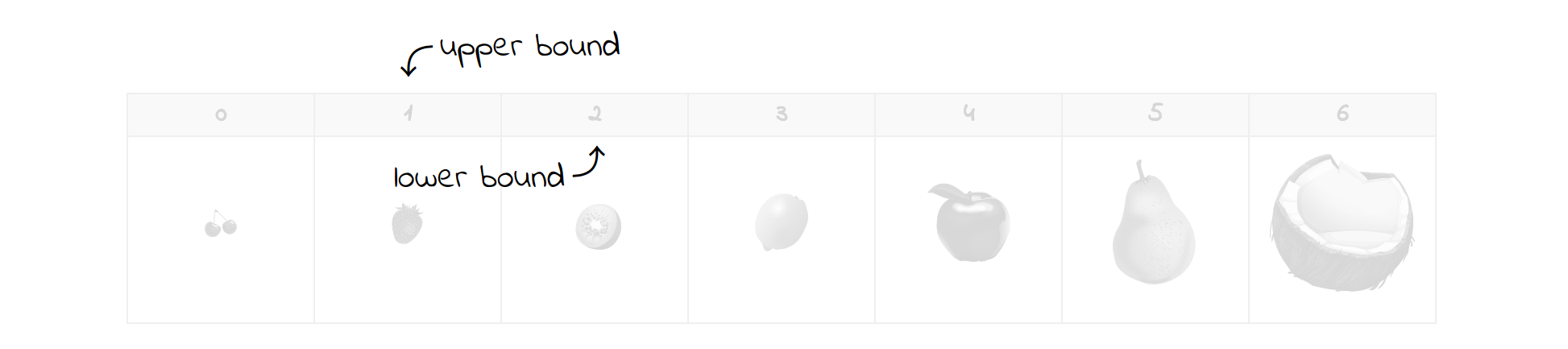
Теперь у вас осталась только половина фруктов, с которых вы начинали. Текущий средний элемент - это действительно та клубника, которую вы искали, что завершает поиск. Если бы это было не так, то вы бы просто соответствующим образом обновили границы и продолжали, пока они не пересекутся. Например, поиск недостающей сливы, которая могла бы находиться между клубникой и киви, завершится следующим результатом:

Обратите внимание, что для поиска нужного элемента требовалось выполнить не так уж много сравнений. В этом и заключается магия бинарного поиска. Даже если вы имеете дело с миллионом элементов, вам потребуется не более нескольких проверок. Это число не превысит логарифма по второму основанию от общего числа элементов из-за сокращения вдвое. Другими словами, количество оставшихся элементов уменьшается наполовину на каждом шаге.

Это возможно, потому что элементы уже отсортированы по размеру. Однако, если бы вы захотели найти фрукты по другому признаку, например, по цвету, вам пришлось бы еще раз отсортировать всю коллекцию. Чтобы избежать дорогостоящей сортировки, вы можете попробовать заранее вычислить разные представления одной и той же коллекции. Это в некоторой степени похоже на создание индекса базы данных .

Подумайте, что произойдет, если вы добавите, удалите или обновите элемент в коллекции. Чтобы бинарный поиск продолжал работать, вам необходимо поддерживать правильный порядок сортировки. Это можно сделать с помощью модуля bisect, о котором вы прочтете в следующем разделе.

Далее в этом руководстве вы увидите, как реализовать алгоритм бинарного поиска в Python. А пока давайте рассмотрим его на примере набора данных IMDb. Обратите внимание, что теперь нужно искать других людей, чем раньше. Это связано с тем, что набор данных должен быть отсортирован для бинарного поиска, который изменяет порядок элементов. Новые элементы расположены примерно по тем же индексам, что и раньше, чтобы измерения были сопоставимы:

Search Term	Element Index	Average Time	Comparisons
(…) Berendse	0	6.52µs	23
Jonathan Samuangte	4,499,997	6.99µs	24
Yorgos Rahmatoulin	9,500,001	6.5µs	23
missing	N/A	7.2µs	23

Ответы приходят практически мгновенно. В среднем бинарному поиску требуется всего несколько микросекунд, чтобы найти один элемент среди всех девяти миллионов! В остальном количество сравнений для выбранных элементов остается практически постоянным, что соответствует следующей формуле:

Для поиска большинства элементов потребуется наибольшее количество сравнений, которое может быть получено из логарифма размера коллекции. И наоборот, в середине есть только один элемент, который можно найти с первой попытки с помощью одного сравнения.

Бинарный поиск - отличный пример метода разделяй и властвуй, который разбивает одну проблему на множество более мелких проблем того же рода. Затем отдельные решения объединяются для получения окончательного ответа. Другим хорошо известным примером этого метода является алгоритм быстрой сортировки.

Примечание: Не путайте принцип "разделяй и властвуй" с динамическим программированием, которое является в чем-то схожим методом.

В отличие от других алгоритмов поиска, бинарный поиск можно использовать не только для простого поиска. Например, он позволяет проверять принадлежность набора, находить наибольшее или наименьшее значение, находить ближайшего соседа целевого значения, выполнять запросы диапазона и многое другое.

Если скорость является главным приоритетом, то бинарный поиск не всегда является лучшим выбором. Существуют еще более быстрые алгоритмы, которые могут использовать преимущества структур данных, основанных на хэшировании. Однако эти алгоритмы требуют много дополнительной памяти, в то время как бинарный поиск предлагает хороший компромисс между пространством и временем.

Поиск на основе хэша

Чтобы ускорить поиск, вам нужно сузить область поиска проблем. Бинарный поиск позволяет достичь этой цели, сокращая вдвое количество кандидатов на каждом шаге. Это означает, что даже если у вас есть миллион элементов, требуется не более двадцати сравнений, чтобы определить, присутствует ли данный элемент, при условии, что все элементы отсортированы.

Самый быстрый способ поиска - это знать, где находится то, что вы ищете. Если бы вы знали точное местоположение элемента в памяти, вы бы получили к нему прямой доступ без необходимости поиска. Сопоставление элемента или (чаще всего) одного из его ключей с расположением элемента в памяти называется хэшированием.

Вы можете рассматривать хэширование не как поиск конкретного элемента, а как вычисление индекса на основе самого элемента. Это работа человека, который хэш-функция, который должен обладать определенными математическими свойствами. Хорошая хэш-функция должна:

• Возьмите произвольные входные данные и преобразуйте их в выходные данные фиксированного размера.
• имеют равномерное распределение значение для смягчения хеш-коллизий.
• Получайте детерминированные результаты.
• Быть односторонней функцией.
• Усиливайте изменения входных сигналов для достижения лавинного эффекта.

В то же время, это не должно быть слишком затратным с точки зрения вычислений, иначе его стоимость перевесит выгоды. Хэш-функция также используется для проверки целостности данных, а также в криптографии.

Структура данных, которая использует эту концепцию для преобразования ключей в значения, называется картой, хэш-таблицей, словарь или ассоциативный массив .

Примечание: В Python есть две встроенные структуры данных, а именно set и dict, которые используют хэш-функцию для поиска элементов. В то время как set хэширует свои элементы, dict использует хэш-функцию для ключей элементов. Чтобы точно узнать, как dict реализован в Python, ознакомьтесь с докладом Раймонда Хеттингера на конференции, посвященной Современным словарям Python..

Другой способ визуализировать хэширование - это представить так называемые группы похожих элементов, сгруппированных по соответствующим ключам. Например, вы можете собирать фрукты в разные ведра в зависимости от цвета:

Кокос и киви отправляются в ведерко с надписью коричневое, а яблоко попадает в ведерко с надписью красное., и так далее. Это позволит вам быстро просмотреть некоторые элементы. В идеале в каждом ведерке должно быть только по одному фрукту. В противном случае вы получите то, что известно как столкновение, что приводит к дополнительной работе.

Примечание: Ячейки, а также их содержимое, как правило, расположены в произвольном порядке.

Давайте поместим имена из набора данных IMDb в словарь, чтобы каждое имя стало ключом, а соответствующее значение - его индексом:

>>> from benchmark import load_names  # Sample code to download
>>> names = load_names('names.txt')
>>> index_by_name = {
...     name: index for index, name in enumerate(names)
... }

После загрузки текстовых названий в виде плоского списка вы можете enumerate() добавить их в словарный запас, чтобы создать сопоставление. Теперь проверить наличие элемента, а также получить его индекс очень просто:

>>> 'Guido van Rossum' in index_by_name
False
>>> 'Arnold Schwarzenegger' in index_by_name
True
>>> index_by_name['Arnold Schwarzenegger']
215

Благодаря хэш-функции, используемой за кулисами, вам вообще не нужно выполнять какой-либо поиск!

Вот как работает алгоритм поиска на основе хэша в наборе данных IMDb:

Search Term	Element Index	Best Time	Average Time	Worst Time
Fred Astaire	0	0.18µs	0.4µs	1.9µs
Alicia Monica	4,500,000	0.17µs	0.4µs	2.4µs
Baoyin Liu	9,500,000	0.17µs	0.4µs	2.6µs
missing	N/A	0.19µs	0.4µs	1.7µs

Это не только сокращает среднее время на порядок по сравнению с и без того быстрой реализацией бинарного поиска на Python, но и обеспечивает стабильную скорость для всех элементов, независимо от того, где они находятся.

Ценой этого увеличения является увеличение объема памяти, потребляемой процессом Python, примерно на 0,5 ГБ, более медленное время загрузки и необходимость поддерживать соответствие этих дополнительных данных содержимому словаря. В свою очередь, поиск выполняется очень быстро, в то время как обновления и вставки выполняются немного медленнее по сравнению со списком.

Еще одно ограничение, которое словари накладывают на свои ключи, заключается в том, что они должны быть хэшируемыми, а их хэш-значения не могут меняться со временем. Вы можете проверить, доступен ли определенный тип данных для хэширования в Python, вызвав для него hash():

>>> key = ['round', 'juicy']
>>> hash(key)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'

Изменяемые коллекции, такие как a list, set, и dict, не поддаются хэшированию. На практике ключи словаря должны быть неизменяемыми, поскольку их хэш-значение часто зависит от некоторых атрибутов ключа. Если бы изменяемая коллекция была доступна для хэширования и могла использоваться в качестве ключа, то ее хэш-значение менялось бы при каждом изменении содержимого. Подумайте, что произошло бы, если бы определенный фрукт изменил цвет из-за созревания. Вы бы искали его не в той корзине!

У хэш-функции есть множество других применений. Например, она используется в криптографии, чтобы избежать хранения паролей в виде обычного текста, а также для проверки целостности данных.

С помощью модуля bisect

Бинарный поиск в Python может быть выполнен с помощью встроенного модуля bisect, который также помогает сохранить список в отсортированном порядке. Он основан на методе деления пополам для нахождения корней функций. Этот модуль содержит шесть функций, разделенных на две категории:

Find Index	Insert Element
bisect()	insort()
bisect_left()	insort_left()
bisect_right()	insort_right()

Эти функции позволяют вам либо найти индекс элемента, либо добавить новый элемент в нужном месте. Те, что в первой строке, являются просто псевдонимами для bisect_right() и insort_right() соответственно. На самом деле вы имеете дело только с четырьмя функциями.

Примечание: Вы несете ответственность за сортировку списка перед передачей его в одну из функций. Если элементы не отсортированы, то, скорее всего, вы получите неверные результаты.

Не мудрствуя лукаво, давайте посмотрим на модуль bisect в действии.

Поиск элемента

Чтобы найти индекс существующего элемента в отсортированном списке, вам нужно bisect_left():

>>> import bisect
>>> sorted_fruits = ['apple', 'banana', 'orange', 'plum']
>>> bisect.bisect_left(sorted_fruits, 'banana')
1

В выходных данных указано, что банан является вторым фруктом в списке, потому что он был найден по индексу 1. Однако, если элемент отсутствует, вы все равно получите его ожидаемую позицию:

>>> bisect.bisect_left(sorted_fruits, 'apricot')
1
>>> bisect.bisect_left(sorted_fruits, 'watermelon')
4

Несмотря на то, что этих фруктов еще нет в списке, вы можете составить представление о том, куда их положить. Например, абрикос должен располагаться между яблоком и бананом, а арбуз должен быть последним элементом. Вы узнаете, был ли найден элемент, выполнив два условия:

1. Соответствует ли размер списка индексу?

2. Является ли значение элемента желаемым?

Это может быть преобразовано в универсальную функцию для поиска элементов по значению:

def find_index(elements, value):
    index = bisect.bisect_left(elements, value)
    if index < len(elements) and elements[index] == value:
        return index

При обнаружении совпадения функция вернет индекс соответствующего элемента. В противном случае она вернет None неявно.

Для поиска по ключу необходимо вести отдельный список ключей. Поскольку это требует дополнительных затрат, стоит заранее рассчитать ключи и использовать их как можно чаще. Вы можете определить вспомогательный класс, чтобы иметь возможность выполнять поиск по разным ключам без большого дублирования кода:

class SearchBy:
    def __init__(self, key, elements):
        self.elements_by_key = sorted([(key(x), x) for x in elements])
        self.keys = [x[0] for x in self.elements_by_key]

Ключ - это функция, передаваемая в качестве первого параметра __init__(). Получив ключ, вы создаете отсортированный список пар ключ-значение, чтобы иметь возможность позже извлекать элемент из его ключа. Представление пар с помощью кортежей гарантирует, что первый элемент каждой пары будет отсортирован. На следующем шаге вы извлекаете ключи, чтобы создать плоский список, подходящий для вашей реализации бинарного поиска на Python.

Далее следует реальный метод поиска элементов по ключу:

class SearchBy:
    def __init__(self, key, elements):
        ...

    def find(self, value):
        index = bisect.bisect_left(self.keys, value)
        if index < len(self.keys) and self.keys[index] == value:
            return self.elements_by_key[index][1]

Этот код делит список отсортированных ключей пополам, чтобы получить индекс элемента по ключу. Если такой ключ существует, то его индекс можно использовать для получения соответствующей пары из ранее вычисленного списка пар ключ-значение. Вторым элементом этой пары является желаемое значение.

Примечание: Это всего лишь иллюстративный пример. Вам будет лучше использовать рекомендуемый рецепт, который указан в официальной документации.

Если бы у вас было несколько бананов, то bisect_left() вернул бы самый левый экземпляр:

>>> sorted_fruits = [
...     'apple',
...     'banana', 'banana', 'banana',
...     'orange',
...     'plum'
... ]
>>> bisect.bisect_left(sorted_fruits, 'banana')
1

Как и ожидалось, чтобы получить самый правый банан, вам нужно будет вызвать bisect_right() или его псевдоним bisect(). Однако эти две функции возвращают на один индекс дальше от фактического крайнего правого банана, что полезно для определения точки вставки нового элемента:

>>> bisect.bisect_right(sorted_fruits, 'banana')
4
>>> bisect.bisect(sorted_fruits, 'banana')
4
>>> sorted_fruits[4]
'orange'

Когда вы объедините код, вы сможете увидеть, сколько у вас получилось бананов:

>>> l = bisect.bisect_left(sorted_fruits, 'banana')
>>> r = bisect.bisect_right(sorted_fruits, 'banana')
>>> r - l
3

Если бы элемент отсутствовал, то и bisect_left(), и bisect_right() возвращали бы один и тот же индекс, что давало бы нулевые значения.

Вставка нового элемента

Другим практическим применением модуля bisect является поддержание порядка расположения элементов в уже отсортированном списке. В конце концов, вы же не захотите сортировать весь список каждый раз, когда вам нужно что-то в него вставить. В большинстве случаев все три функции могут использоваться взаимозаменяемо:

>>> import bisect
>>> sorted_fruits = ['apple', 'banana', 'orange']
>>> bisect.insort(sorted_fruits, 'apricot')
>>> bisect.insort_left(sorted_fruits, 'watermelon')
>>> bisect.insort_right(sorted_fruits, 'plum')
>>> sorted_fruits
['apple', 'apricot', 'banana', 'orange', 'plum', 'watermelon']

Вы не увидите никакой разницы, пока в вашем списке не будет дубликатов. Но даже тогда это не станет очевидным, пока эти дубликаты являются простыми значениями. Добавление еще одного банана слева даст тот же эффект, что и его добавление справа.

Чтобы заметить разницу, вам нужен тип данных, объекты которого могут иметь уникальные идентификаторы, несмотря на наличие одинаковых значений. Давайте определим тип Person, используя @dataclass декоратор, который был представлен в Python 3.7:

from dataclasses import dataclass, field

@dataclass
class Person:
    name: str
    number: int = field(compare=False)

    def __repr__(self):
        return f'{self.name}({self.number})'

У человека есть name и произвольный number, присвоенный ему. Исключая поле number из теста на равенство, вы делаете двух людей равными, даже если у них разные значения этого атрибута:

>>> p1 = Person('John', 1)
>>> p2 = Person('John', 2)
>>> p1 == p2
True

С другой стороны, эти две переменные относятся к совершенно разным объектам, что позволяет вам проводить различие между ними:

>>> p1 is p2
False
>>> p1
John(1)
>>> p2
John(2)

Переменные p1 и p2 действительно являются разными объектами.

Обратите внимание, что экземпляры класса данных по умолчанию несопоставимы, что не позволяет использовать для них алгоритм деления пополам:

>>> alice, bob = Person('Alice', 1), Person('Bob', 1)
>>> alice < bob
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: '<' not supported between instances of 'Person' and 'Person'

Python не умеет упорядочивать alice и bob, потому что они являются объектами пользовательского класса. Традиционно, вы бы реализовали магический метод .__lt__() в своем классе, который обозначает меньше, чем, чтобы сообщить интерпретатору, как сравнивать такие элементы. Однако @dataclass декоратор принимает несколько необязательных логических флагов. Одним из них является order, который приводит к автоматической генерации магических методов для сравнения, если установлено значение True:

@dataclass(order=True)
class Person:
    ...

В свою очередь, это позволяет вам сравнить двух людей и решить, кто из них стоит на первом месте:

>>> alice < bob
True
>>> bob < alice
False

Наконец, вы можете воспользоваться свойствами name и number, чтобы увидеть, где различные функции добавляют новых пользователей в список:

>>> sorted_people = [Person('John', 1)]
>>> bisect.insort_left(sorted_people, Person('John', 2))
>>> bisect.insort_right(sorted_people, Person('John', 3))
>>> sorted_people
[John(2), John(1), John(3)]

Цифры в круглых скобках после имен указывают порядок вставки. Вначале был только один John, который получил номер 1. Затем вы добавили его дубликат слева, а позже еще один справа.

Реализация бинарного поиска в Python

Имейте в виду, что вам, вероятно, не стоит внедрять алгоритм, если у вас нет на то веских причин. Вы сэкономите время и не будете вынуждены изобретать велосипед. Скорее всего, библиотечный код является зрелым, уже протестированным реальными пользователями в рабочей среде и обладает обширной функциональностью, предоставляемой несколькими авторами.

Тем не менее, иногда имеет смысл засучить рукава и сделать это самостоятельно. Возможно, в вашей компании действует политика, запрещающая использование определенных библиотек с открытым исходным кодом по причинам лицензирования или безопасности. Возможно, вы не можете позволить себе еще одну зависимость из-за нехватки памяти или пропускной способности сети. Наконец, самостоятельное написание кода может стать отличным инструментом обучения!

Большинство алгоритмов можно реализовать двумя способами:

1. Итеративно
2. Рекурсивно

Однако из этого правила есть исключения. Одним из примечательных примеров является функция Аккермана, которая может быть выражена только в терминах рекурсии.

Прежде чем вы продолжите, убедитесь, что вы хорошо разбираетесь в алгоритме бинарного поиска. Вы можете обратиться к более ранней части этого руководства для краткого ознакомления.

Итеративно

Итеративная версия алгоритма включает цикл, который будет повторять некоторые шаги до тех пор, пока не будет выполнено условие остановки. Давайте начнем с реализации функции, которая будет искать элементы по значению и возвращать их индекс:

def find_index(elements, value):
    ...

Вы собираетесь повторно использовать эту функцию позже.

Предполагая, что все элементы отсортированы, вы можете установить нижнюю и верхнюю границы на противоположных концах последовательности:

def find_index(elements, value):
    left, right = 0, len(elements) - 1

Теперь вы хотите определить средний элемент, чтобы увидеть, имеет ли он желаемое значение. Вычисление среднего индекса можно выполнить, взяв среднее значение для обеих границ:

def find_index(elements, value):
    left, right = 0, len(elements) - 1
    middle = (left + right) // 2

Обратите внимание, как целочисленное деление помогает обрабатывать как нечетное, так и четное количество элементов в ограниченном диапазоне, используя для получения результата. В зависимости от того, как вы собираетесь обновить границы и определить условие остановки, вы также можете использовать функцию ceiling.

Далее вы либо завершаете, либо разбиваете последовательность на две части и продолжаете поиск в одной из получившихся половин:

def find_index(elements, value):
    left, right = 0, len(elements) - 1
    middle = (left + right) // 2

    if elements[middle] == value:
        return middle

    if elements[middle] < value:
        left = middle + 1
    elif elements[middle] > value:
        right = middle - 1

Если элемент в середине соответствует, то вы возвращаете его индекс. В противном случае, если он был слишком мал, вам нужно переместить нижнюю границу вверх. Если он был слишком большим, то вам нужно сдвинуть верхнюю границу вниз.

Чтобы продолжить, вам нужно заключить большинство шагов в цикл, который остановится, когда нижняя граница перейдет верхнюю:

def find_index(elements, value):
    left, right = 0, len(elements) - 1

    while left <= right:
        middle = (left + right) // 2

        if elements[middle] == value:
            return middle

        if elements[middle] < value:
            left = middle + 1
        elif elements[middle] > value:
            right = middle - 1

Другими словами, вы хотите выполнять итерацию до тех пор, пока нижняя граница не окажется ниже верхней или равной ей. В противном случае совпадения не было, и функция возвращает None неявно.

Поиск по ключу сводится к просмотру атрибутов объекта, а не его буквального значения. Ключом может быть, например, количество символов в названии фрукта. Вы можете адаптировать find_index() для принятия и использования параметра key:

def find_index(elements, value, key):
    left, right = 0, len(elements) - 1

    while left <= right:
        middle = (left + right) // 2
        middle_element = key(elements[middle])

        if middle_element == value:
            return middle

        if middle_element < value:
            left = middle + 1
        elif middle_element > value:
            right = middle - 1

Однако вы также должны помнить, что список нужно отсортировать, используя тот же key, с помощью которого вы собираетесь выполнять поиск:

>>> fruits = ['orange', 'plum', 'watermelon', 'apple']
>>> fruits.sort(key=len)
>>> fruits
['plum', 'apple', 'orange', 'watermelon']
>>> fruits[find_index(fruits, key=len, value=10)]
'watermelon'
>>> print(find_index(fruits, key=len, value=3))
None

В приведенном выше примере watermelon был выбран потому, что его название состоит ровно из десяти символов, в то время как ни у одного фрукта в списке нет названий, состоящих из трех букв.

Это здорово, но в то же время вы только что потеряли возможность поиска по значению. Чтобы исправить это, вы могли бы присвоить key значение по умолчанию None, а затем проверить, было ли оно задано или нет. Однако в более упрощенном решении вы всегда хотели бы вызывать key. По умолчанию это будет функция идентификации, возвращающая сам элемент:

def identity(element):
    return element

def find_index(elements, value, key=identity):
    ...

В качестве альтернативы вы могли бы определить функцию идентификации, встроенную в анонимное лямбда-выражение:

def find_index(elements, value, key=lambda x: x):
    ...

find_index() отвечает только на один вопрос. Есть еще два других: “Есть ли это?” и “Что это такое?” Чтобы ответить на эти два вопроса, вы можете дополнить их:

def find_index(elements, value, key):
    ...

def contains(elements, value, key=identity):
    return find_index(elements, value, key) is not None

def find(elements, value, key=identity):
    index = find_index(elements, value, key)
    return None if index is None else elements[index]

С помощью этих трех функций вы можете рассказать об элементе практически все. Однако вы все еще не рассмотрели дубликаты в своей реализации. Что, если бы у вас была группа людей, и у некоторых из них было бы общее имя или фамилия? Например, среди людей может быть семья Smith или несколько парней по имени John:

people = [
    Person('Bob', 'Williams'),
    Person('John', 'Doe'),
    Person('Paul', 'Brown'),
    Person('Alice', 'Smith'),
    Person('John', 'Smith'),
]

Чтобы смоделировать тип Person, вы можете изменить класс данных, определенный ранее:

from dataclasses import dataclass

@dataclass(order=True)
class Person:
    name: str
    surname: str

Обратите внимание на использование атрибута order, позволяющего автоматически генерировать магические методы для сравнения экземпляров класса по всем полям. В качестве альтернативы вы можете предпочесть воспользоваться namedtuple,, который имеет более короткий синтаксис:

from collections import namedtuple
Person = namedtuple('Person', 'name surname')

Оба определения хороши и взаимозаменяемы. У каждого человека есть name и surname атрибуты. Для сортировки и поиска по одному из них вы можете удобно определить ключевую функцию с помощью attrgetter(), доступного во встроенном модуле operator:

>>> from operator import attrgetter
>>> by_surname = attrgetter('surname')
>>> people.sort(key=by_surname)
>>> people
[Person(name='Paul', surname='Brown'),
 Person(name='John', surname='Doe'),
 Person(name='Alice', surname='Smith'),
 Person(name='John', surname='Smith'),
 Person(name='Bob', surname='Williams')]

Обратите внимание, что теперь люди отсортированы по фамилиям в порядке возрастания. Есть John Smith и Alice Smith, но бинарный поиск по фамилии Smith в настоящее время дает вам только один произвольный результат:

>>> find(people, key=by_surname, value='Smith')
Person(name='Alice', surname='Smith')

Чтобы имитировать функции модуля bisect, показанного ранее, вы можете написать свою собственную версию модулей bisect_left() и bisect_right(). Прежде чем найти самый левый экземпляр повторяющегося элемента, вы хотите определить, существует ли такой элемент вообще:

def find_leftmost_index(elements, value, key=identity):
    index = find_index(elements, value, key)
    if index is not None:
        ...
    return index

Если какой-то индекс найден, то вы можете посмотреть влево и продолжать движение, пока не наткнетесь на элемент с другим ключом или пока элементов больше не останется:

def find_leftmost_index(elements, value, key=identity):
    index = find_index(elements, value, key)
    if index is not None:
        while index >= 0 and key(elements[index]) == value:
            index -= 1
        index += 1
    return index

Как только вы пройдете мимо крайнего левого элемента, вам нужно переместить индекс на одну позицию вправо.

Поиск самого правого экземпляра очень похож, но вам нужно изменить условия:

def find_rightmost_index(elements, value, key=identity):
    index = find_index(elements, value, key)
    if index is not None:
        while index < len(elements) and key(elements[index]) == value:
            index += 1
        index -= 1
    return index

Теперь вместо того, чтобы идти налево, вы идете направо до конца списка. Использование обеих функций позволяет найти все вхождения повторяющихся элементов:

def find_all_indices(elements, value, key=identity):
    left = find_leftmost_index(elements, value, key)
    right = find_rightmost_index(elements, value, key)
    if left and right:
        return set(range(left, right + 1))
    return set()

Эта функция всегда возвращает набор. Если элемент не найден, то набор будет пустым. Если элемент уникален, то набор будет состоять только из одного индекса. В противном случае в наборе будет несколько индексов.

В заключение, вы можете определить еще более абстрактные функции для завершения вашего бинарного поиска в библиотеке Python:

def find_leftmost(elements, value, key=identity):
    index = find_leftmost_index(elements, value, key)
    return None if index is None else elements[index]

def find_rightmost(elements, value, key=identity):
    index = find_rightmost_index(elements, value, key)
    return None if index is None else elements[index]

def find_all(elements, value, key=identity):
    return {elements[i] for i in find_all_indices(elements, value, key)}

Это позволяет не только точно определить местоположение элементов в списке, но и получить доступ к этим элементам. Вы можете задавать очень конкретные вопросы:

Is it there?	Where is it?	What is it?
contains()	find_index()	find()
	find_leftmost_index()	find_leftmost()
	find_rightmost_index()	find_rightmost()
	find_all_indices()	find_all()

Полный код этой библиотеки Python для бинарного поиска можно найти по ссылке ниже:

Рекурсивно

Для простоты вы будете рассматривать только рекурсивную версию contains(), которая сообщает вам, был ли элемент найден.

Примечание: Мое любимое определение рекурсии было дано в эпизоде из серии Fun Fun Function о функциональном программировании на JavaScript:

“Рекурсия - это когда функция вызывает саму себя до тех пор, пока этого не произойдет”.

— Маттиас Петтер Йоханссон

Наиболее простым подходом было бы использовать итеративную версию бинарного поиска и использовать оператор нарезки, чтобы сократить список:

def contains(elements, value):
    left, right = 0, len(elements) - 1

    if left <= right:
        middle = (left + right) // 2

        if elements[middle] == value:
            return True

        if elements[middle] < value:
            return contains(elements[middle + 1:], value)
        elif elements[middle] > value:
            return contains(elements[:middle], value)

    return False

Вместо зацикливания вы проверяете условие один раз и иногда вызываете ту же функцию в меньшем списке. Что в этом может пойти не так? Что ж, оказывается, что при нарезке генерируется копий ссылок на элементы, что может привести к заметным затратам памяти и вычислительным затратам.

Чтобы избежать копирования, вы можете повторно использовать один и тот же список, но при необходимости передавать функции разные границы:

def contains(elements, value, left, right):
    if left <= right:
        middle = (left + right) // 2

        if elements[middle] == value:
            return True

        if elements[middle] < value:
            return contains(elements, value, middle + 1, right)
        elif elements[middle] > value:
            return contains(elements, value, left, middle - 1)

    return False

Недостатком является то, что каждый раз, когда вы хотите вызвать эту функцию, вам приходится проходить начальные границы, проверяя их правильность:

>>> sorted_fruits = ['apple', 'banana', 'orange', 'plum']
>>> contains(sorted_fruits, 'apple', 0, len(sorted_fruits) - 1)
True

Если бы вы допустили ошибку, то, возможно, этот элемент не был бы найден. Вы можете улучшить это, используя аргументы функции по умолчанию или введя вспомогательную функцию, которая делегирует рекурсивную функцию:

def contains(elements, value):
    return recursive(elements, value, 0, len(elements) - 1)

def recursive(elements, value, left, right):
    ...

Идя дальше, вы можете предпочесть вложить одну функцию в другую, чтобы скрыть технические детали и воспользоваться преимуществами повторного использования переменных из внешней области:

def contains(elements, value):
    def recursive(left, right):
        if left <= right:
            middle = (left + right) // 2
            if elements[middle] == value:
                return True
            if elements[middle] < value:
                return recursive(middle + 1, right)
            elif elements[middle] > value:
                return recursive(left, middle - 1)
        return False
    return recursive(0, len(elements) - 1)

Внутренняя функция recursive() может обращаться как к параметрам elements, так и к параметрам value, даже если они определены во вложенной области. Жизненный цикл и видимость переменных в Python определяются так называемым правилом LEGB, которое предписывает интерпретатору искать символы в следующем порядке:

1. Локальная область применения
2. Включающий область применения
3. Глобальная область применения
4. Встроенные символы

Это позволяет получать доступ к переменным, определенным во внешней области видимости, из вложенных блоков кода.

Выбор между итеративной и рекурсивной реализацией часто является конечным результатом соображений производительности, удобства, а также личного вкуса. Однако рекурсия также сопряжена с определенными рисками, что является одной из тем следующего раздела.

Освещение сложных деталей

Вот что говорит автор книги Искусство компьютерного программирования о реализации алгоритма бинарного поиска:

“Хотя основная идея бинарного поиска сравнительно проста, детали могут быть на удивление сложными, и многие хорошие программисты делали это неправильно при первых же попытках”.

— Дональд Кнут

Если это недостаточно сильно удержит вас от идеи написать алгоритм самостоятельно, то, возможно, это поможет. В стандартной библиотеке в Java была небольшая ошибка в реализации бинарного поиска, которая оставалась нераскрытой в течение десятилетия! Но сама ошибка возникла гораздо раньше этого.

Примечание: Однажды я стал жертвой алгоритма бинарного поиска во время технической проверки. Нужно было решить пару задач по кодированию, в том числе и по бинарному поиску. Угадайте, какой из них мне не удалось выполнить? Да.

Приведенный ниже список не является исчерпывающим, но в то же время в нем не говорится о таких распространенных ошибках, как забывание отсортировать список.

Переполнение целого числа

Это ошибка Java, о которой только что упоминалось. Если вы помните, алгоритм бинарного поиска Python проверяет средний элемент ограниченного диапазона в отсортированной коллекции. Но как именно выбирается этот средний элемент? Обычно вы берете среднее значение нижней и верхней границ, чтобы найти средний индекс:

middle = (left + right) // 2

Этот метод вычисления среднего значения отлично работает в подавляющем большинстве случаев. Однако, как только набор элементов становится достаточно большим, сумма обеих границ не будет соответствовать целочисленному типу данных. Это будет больше максимально допустимого значения для целых чисел.

В таких ситуациях некоторые языки программирования могут выдавать ошибку, которая немедленно останавливает выполнение программы. К сожалению, это не всегда так. Например, Java молча игнорирует эту проблему, позволяя значению изменяться и становиться каким-то случайным числом. Вы будете знать о проблеме только до тех пор, пока результирующее число не окажется отрицательным, что приведет к IndexOutOfBoundsException.

Вот пример, демонстрирующий такое поведение в jshell, который является чем-то вроде интерактивного интерпретатора для Java:

jshell> var a = Integer.MAX_VALUE
a ==> 2147483647

jshell> a + 1
$2 ==> -2147483648

Более безопасным способом найти средний индекс может быть сначала вычисление смещения, а затем добавление его к нижней границе:

middle = left + (right - left) // 2

Даже если оба значения будут максимальными, сумма в приведенной выше формуле никогда не будет равна нулю. Есть еще несколько способов, но хорошая новость заключается в том, что вам не нужно беспокоиться ни об одном из них, потому что в Python нет ошибки переполнения целого числа. Нет никакого верхнего предела того, насколько большими могут быть целые числа, отличные от вашей памяти:

>>> 2147483647**7
210624582650556372047028295576838759252690170086892944262392971263

Однако есть одна загвоздка. Когда вы вызываете функции из библиотеки, этот код может быть подвержен ограничениям языка Си и все равно вызывать переполнение. В Python существует множество библиотек, основанных на языке Си. Вы могли бы даже создать свой собственный модуль расширения C или загрузить динамически связываемую библиотеку в Python с помощью ctypes.

Переполнение стека

Проблема переполнения стека теоретически может быть связана с рекурсивной реализацией бинарного поиска. Большинство языков программирования накладывают ограничение на количество вызовов вложенных функций. Каждый вызов связан с обратным адресом, хранящимся в стеке. В Python ограничение по умолчанию составляет несколько тысяч уровней таких вызовов:

>>> import sys
>>> sys.getrecursionlimit()
1000

Этого будет недостаточно для большого количества рекурсивных функций. Однако очень маловероятно, что двоичный поиск в Python когда-либо потребует большего из-за его логарифмической природы. Вам понадобится коллекция из двух в степени трех тысяч элементов. Это число содержит более девятисот цифр!

Тем не менее, все еще возможно возникновение ошибки бесконечной рекурсии, если условие остановки указано неправильно из-за ошибки. В таком случае бесконечная рекурсия в конечном итоге приведет к переполнению стека.

Примечание: Ошибка переполнения стека очень распространена среди языков с ручным управлением памятью. Люди часто загугливали эти ошибки, чтобы узнать, были ли у кого-то еще похожие проблемы, что дало название популярному сайту вопросов и ответов для программистов ..

Вы можете временно отменить или уменьшить ограничение на рекурсию, чтобы имитировать ошибку переполнения стека. Обратите внимание, что эффективное ограничение будет меньше из-за функций, которые должна вызывать среда выполнения Python:

>>> def countup(limit, n=1):
...     print(n)
...     if n < limit:
...         countup(limit, n + 1)
...
>>> import sys
>>> sys.setrecursionlimit(7)  # Actual limit is 3
>>> countup(10)
1
2
3
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 4, in countup
  File "<stdin>", line 4, in countup
  File "<stdin>", line 2, in countup
RecursionError: maximum recursion depth exceeded while calling a Python object

Рекурсивная функция была вызвана три раза, прежде чем стек заполнился. Оставшиеся четыре вызова, должно быть, были выполнены интерактивным интерпретатором. Если вы запустите тот же код в PyCharm или альтернативной оболочке Python, то вы можете получить другой результат.

Повторяющиеся элементы

Вы знаете о возможности наличия повторяющихся элементов в списке и знаете, как с ними бороться. Это просто для того, чтобы подчеркнуть, что обычный бинарный поиск в Python может не дать детерминированных результатов. В зависимости от того, как был отсортирован список или сколько в нем элементов, вы получите другой ответ:

>>> from search.binary import *
>>> sorted_fruits = ['apple', 'banana', 'banana', 'orange']
>>> find_index(sorted_fruits, 'banana')
1
>>> sorted_fruits.append('plum')
>>> find_index(sorted_fruits, 'banana')
2

В списке есть два банана. Сначала вызов find_index() возвращает левый банан. Однако добавление совершенно не связанного элемента в конец списка приводит к тому, что один и тот же вызов приводит к другому результату. banana.

Тот же принцип, известный как стабильность алгоритма, применим к алгоритмам сортировки. Некоторые из них стабильны, что означает, что они не изменяют взаимное расположение эквивалентных элементов. Другие не дают таких гарантий. Если вам когда-нибудь понадобится отсортировать элементы по нескольким критериям, то для сохранения стабильности всегда следует начинать с наименее значимого ключа.

Округление с плавающей запятой

До сих пор вы искали только фрукты или людей, но как насчет цифр? Они не должны отличаться друг от друга, верно? Давайте составим список чисел с плавающей запятой с шагом 0.1, используя понимание списка .:

>>> sorted_numbers = [0.1*i for i in range(1, 4)]

Список должен содержать числа, равные одной десятой, двум десятым и трем десятым. Удивительно, но из этих трех чисел можно найти только два:

>>> from search.binary import contains
>>> contains(sorted_numbers, 0.1)
True
>>> contains(sorted_numbers, 0.2)
True
>>> contains(sorted_numbers, 0.3)
False

Это не проблема, связанная строго с бинарным поиском в Python, поскольку встроенный линейный поиск совместим с ним:

>>> 0.1 in sorted_numbers
True
>>> 0.2 in sorted_numbers
True
>>> 0.3 in sorted_numbers
False

Это даже не проблема, связанная с Python, а скорее с тем, как числа с плавающей запятой представлены в памяти компьютера. Это определено стандартом IEEE 754 для арифметики с плавающей запятой. Не вдаваясь в подробности, отметим, что некоторые десятичные числа не имеют конечного представления в двоичной форме. Из-за ограниченной памяти эти числа округляются , что приводит к ошибке округления с плавающей запятой .

Примечание: Если вам требуется максимальная точность, то избегайте чисел с плавающей запятой. Они отлично подходят для инженерных целей. Однако при проведении денежных операций нежелательно, чтобы накапливались ошибки округления. Рекомендуется уменьшить все цены и суммы до наименьших единиц, таких как центы или пенни, и рассматривать их как целые числа.

Кроме того, многие языки программирования поддерживают числа с фиксированной запятой, такие как десятичный тип в Python. Это позволяет вам контролировать, когда и как происходит округление.

Если вам все-таки нужно работать с числами с плавающей запятой, то вам следует заменить точное сопоставление на приблизительное сравнение. Давайте рассмотрим две переменные с немного отличающимися значениями:

>>> a = 0.3
>>> b = 0.1 * 3
>>> b
0.30000000000000004
>>> a == b
False

Обычное сравнение дает отрицательный результат, хотя оба значения практически идентичны. К счастью, в Python есть функция, которая проверяет, близки ли два значения друг к другу в пределах некоторой небольшой окрестности:

>>> import math
>>> math.isclose(a, b)
True

Это соседство, представляющее собой максимальное расстояние между значениями, может быть скорректировано при необходимости:

>>> math.isclose(a, b, rel_tol=1e-16)
False

Вы можете использовать эту функцию для выполнения бинарного поиска в Python следующим образом:

import math

def find_index(elements, value):
    left, right = 0, len(elements) - 1

    while left <= right:
        middle = (left + right) // 2

        if math.isclose(elements[middle], value):
            return middle

        if elements[middle] < value:
            left = middle + 1
        elif elements[middle] > value:
            right = middle - 1

С другой стороны, эта реализация бинарного поиска в Python специфична только для чисел с плавающей запятой. Вы не смогли бы использовать ее для поиска чего-либо еще, не получив ошибку.

Анализ пространственно-временной сложности бинарного поиска

Следующий раздел не будет содержать кода и некоторых математических понятий.

В вычислительной технике вы можете оптимизировать производительность практически любого алгоритма за счет увеличения использования памяти. Например, вы видели, что поиск по хэшу в наборе данных IMDb требует дополнительных 0,5 ГБ памяти для достижения беспрецедентной скорости.

И наоборот, для экономии полосы пропускания вы могли бы сжать видеопоток перед отправкой по сети, увеличив объем выполняемой работы. Это явление известно как компромисс между пространством и временем и полезно при оценке сложности алгоритма .

Пространственно-временная сложность

Вычислительная сложность - это относительный показатель того, сколько ресурсов требуется алгоритму для выполнения своей работы. Ресурсы включают в себя время вычислений, а также объем используемой памяти. Сравнение сложности различных алгоритмов позволяет вам принять обоснованное решение о том, какой из них лучше в данной ситуации.

Примечание: Алгоритмы, которым не нужно выделять больше памяти, чем уже потребляют их входные данные, называются встроенными, или in-situ, алгоритмы. Это приводит к изменению исходных данных, что иногда может иметь нежелательные побочные эффекты.

Вы рассмотрели несколько алгоритмов поиска и их среднюю производительность на большом наборе данных. Из этих измерений ясно, что бинарный поиск выполняется быстрее, чем линейный. Вы даже можете сказать, по какому коэффициенту.

Однако, если бы вы провели те же измерения в другой среде, вы, вероятно, получили бы незначительные или, возможно, совершенно другие результаты. Существуют невидимые факторы, которые могут повлиять на ваш тест. Кроме того, такие измерения не всегда выполнимы. Итак, как вы можете быстро и объективно сравнить временные сложности?

Первый шаг - разбить алгоритм на более мелкие части и найти ту, которая выполняет наибольшую работу. Скорее всего, это будет какая-то элементарная операция, которая часто вызывается и выполнение которой занимает примерно одинаковое время. Для алгоритмов поиска такой операцией может быть сравнение двух элементов.

Установив это, вы можете теперь проанализировать алгоритм. Чтобы определить временную сложность, вы хотите описать зависимость между количеством выполненных элементарных операций и размером входных данных. Формально такая зависимость является математической функцией. Однако вам неинтересно искать ее точную алгебраическую формулу, а скорее оценить ее общую форму.

Существует несколько хорошо известных классов функций, к которым относится большинство алгоритмов. Классифицировав алгоритм в соответствии с одним из них, вы можете оценить его по шкале:

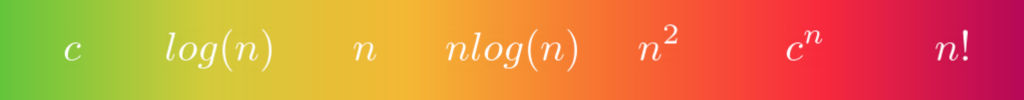Общие классы временной сложности

Эти классы показывают, как увеличивается количество элементарных операций с увеличением размера входных данных. Слева направо:

• Константа
• Логарифмическая
• Линейная
• Квазилинейная
• Квадратичная
• Экспоненциальная
• Факториальная

Это может дать вам представление о производительности рассматриваемого алгоритма. Наиболее желательной является постоянная сложность, независимо от размера входных данных. Логарифмическая сложность все еще довольно высока, что указывает на использование метода "разделяй и властвуй". Чем дальше вправо по этой шкале, тем сложнее алгоритм, поскольку ему предстоит выполнить больше работы.

Когда вы говорите о временной сложности, вы обычно имеете в виду асимптотическую сложность , которая описывает поведение при очень больших наборах данных. Это упрощает формулу функции, исключая все члены и коэффициенты, кроме того, который растет быстрее всего (например, n в квадрате).

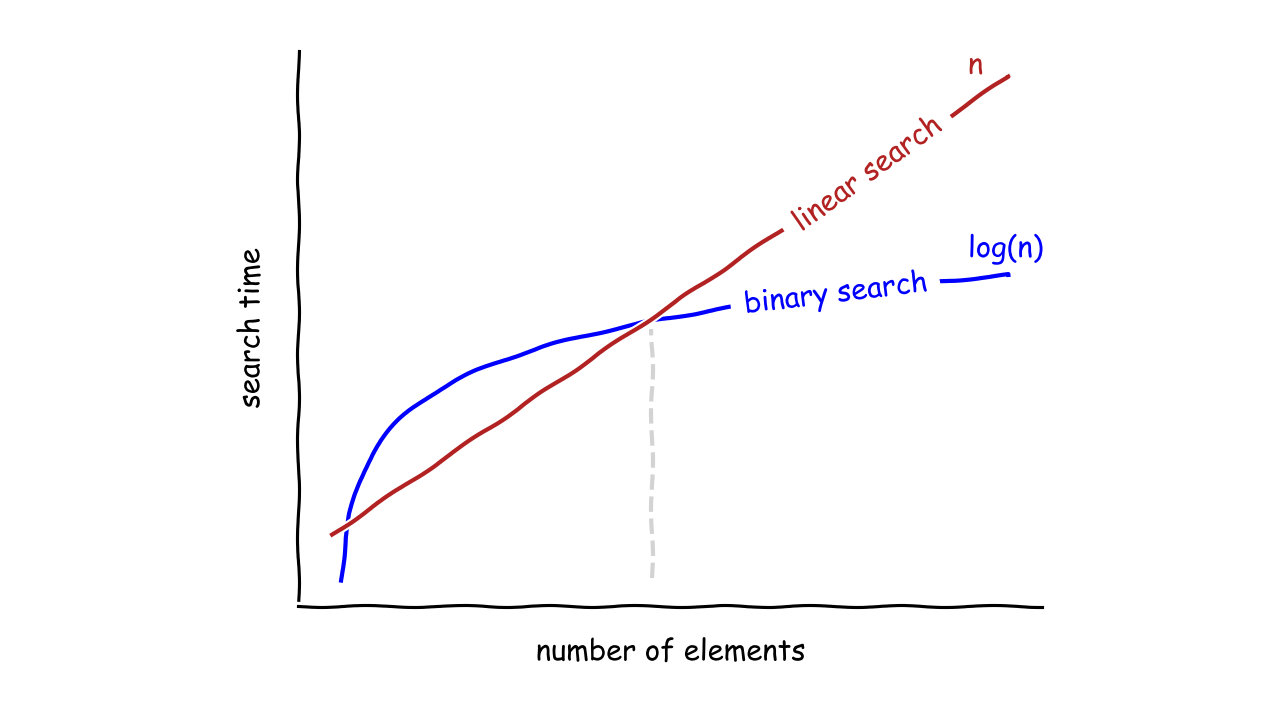
Однако одна функция не предоставляет достаточно информации для точного сравнения двух алгоритмов. Временная сложность может варьироваться в зависимости от объема данных. Например, алгоритм бинарного поиска похож на двигатель с турбонаддувом, который создает давление до того, как будет готов к подаче мощности. С другой стороны, алгоритм линейного поиска быстр с самого начала, но быстро достигает своей максимальной мощности и в конечном итоге проигрывает гонку:

С точки зрения скорости алгоритм бинарного поиска начинает опережать линейный поиск, когда в коллекции появляется определенное количество элементов. Для небольших коллекций линейный поиск может быть лучшим выбором.

Примечание: Обратите внимание, что один и тот же алгоритм может иметь различную оптимистическую, пессимистическую и среднюю временную сложность. Например, в лучшем случае алгоритм линейного поиска найдет элемент по первому индексу после выполнения всего одного сравнения.

С другой стороны, ему придется сравнить эталонное значение со всеми элементами в коллекции. На практике вы хотите знать пессимистическую сложность алгоритма.

Существует несколько математических обозначений асимптотической сложности, которые используются для сравнения алгоритмов. На сегодняшний день наиболее популярным является обозначение с большой буквы О.

Обозначение большой буквы О

Обозначение с большой буквы О представляет наихудший сценарий асимптотической сложности. Хотя это может показаться довольно пугающим, вам не обязательно знать формальное определение. Интуитивно понятно, что это очень приблизительный показатель скорости роста в конце функции, который описывает сложность. Вы произносите это как “большое о” чего-то такого:

Это “что-то” обычно зависит от размера данных или просто от цифры “один”, которая обозначает константу. Например, алгоритм линейного поиска имеет временную сложность O(n), в то время как поиск на основе хэша имеет сложность O(1).

Примечание: Когда вы говорите, что некоторый алгоритм имеет сложность O(f(n)), где n - это размер входных данных, то это означает, что функция f(n) является верхней границей графика такой сложности. Другими словами, фактическая сложность этого алгоритма не будет расти быстрее, чем f(n), умноженное на некоторую константу, когда n приближается к бесконечности.

В реальной жизни обозначение Big O используется менее формально как в качестве верхней, так и в качестве нижней границы. Это полезно для классификации и сравнения алгоритмов, не беспокоясь о точных формулах функций.

Сложность бинарного поиска

Вы сможете оценить асимптотическую временную сложность бинарного поиска, определив количество сравнений в наихудшем случае - когда элемент отсутствует — в зависимости от размера входных данных. Вы можете подойти к этой задаче тремя различными способами:

1. Табличный
2. Графический
3. Аналитический

Табличный метод заключается в сборе эмпирических данных, сведении их в таблицу и попытке угадать формулу по выборочным значениям:

Количество элементов	Количество сравнений
0	0
1	1
2	2
3	2
4	3
5	3
6	3
7	3
8	4

Количество сравнений растет по мере увеличения количества элементов в коллекции, но темпы роста медленнее, чем если бы это была линейная функция. Это свидетельствует о хорошем алгоритме, который может масштабироваться с учетом данных.

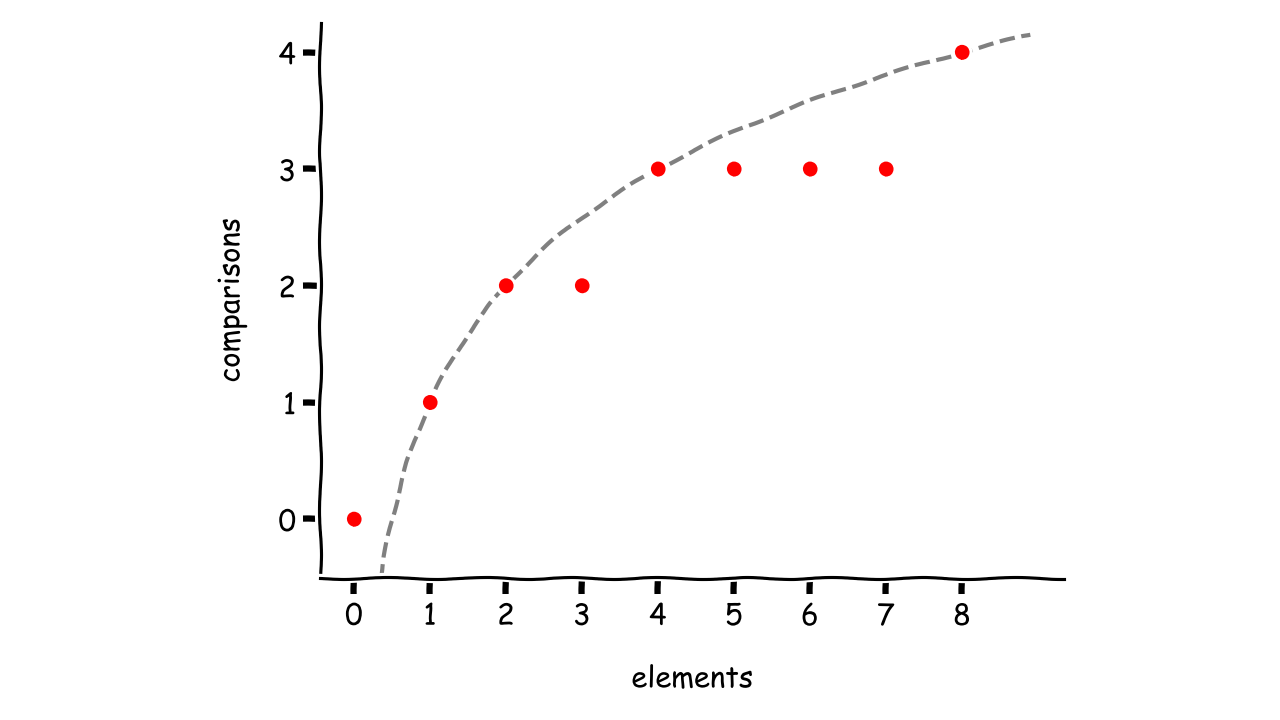
Если это вам не поможет, вы можете попробовать графический метод , который визуализирует выборочные данные, рисуя график:

Кажется, что точки данных накладываются друг на друга кривой, но у вас недостаточно информации, чтобы дать окончательный ответ. Это может быть многочлен, график которого поворачивается вверх и вниз для больших входных данных.

Используя аналитический подход, вы можете выбрать некоторую взаимосвязь и искать закономерности. Например, вы могли бы изучить, как уменьшается количество элементов на каждом шаге алгоритма:

Сравнение	Количество элементов
-	n
1st	n/2
2nd	n/4
3rd	n/8
⋮	⋮
k-th	n/2 k

В начале вы начинаете со всей коллекции из n элементов. После первого сравнения у вас остается только половина из них. Затем у вас остается четверть и так далее. Закономерность, вытекающая из этого наблюдения, заключается в том, что после k-госравнения, остается n/2 k элементов. Переменная k - это ожидаемое количество элементарных операций.

После всех k сравнений элементов больше не останется. Однако, когда вы сделаете один шаг назад, то есть k - 1, останется ровно один элемент. Это даст вам удобное уравнение:

Умножьте обе части уравнения на знаменатель, затем возьмите логарифм по второму основанию результата и сдвиньте оставшуюся константу вправо. Вы только что нашли формулу для сложности бинарного поиска, которая составляет порядка O(log(n)).

Заключение

Теперь вы знаете алгоритм бинарного поиска вдоль и поперек. Вы можете безупречно реализовать его самостоятельно или воспользоваться стандартной библиотекой на Python. Ознакомившись с концепцией пространственно-временной сложности, вы сможете выбрать наилучший алгоритм поиска для данной ситуации.

Теперь вы можете:

• Используйте модуль bisect для выполнения бинарного поиска в Python
• Реализовать бинарный поиск в Python рекурсивно и итеративно
• Распознавать и исправлять дефекты в реализации бинарного поиска на Python
• Проанализируйте пространственно-временную сложность алгоритма бинарного поиска
• Поиск выполняется даже быстрее, чем бинарный поиск

Back to Top